Определение 1. Для любого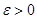 
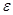- окрестностью точки 
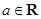называется множество
.
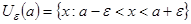В случае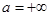 
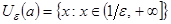, а в случае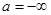 
.
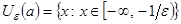Определение 2. Проколотой 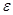-окрестностью точки 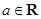называется множество, получающееся удалением точки 
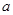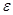из ее -окрестности:
.
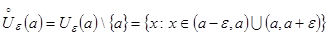Определение 3. Точка 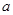называется внутренней точкой множества 
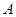, если существует 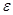-окрестность 
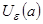, целиком принадлежащая .
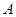Определение 4. Точка 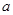называется граничной точкой множества 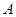, если в каждой ее окрестности существуют точки как принадлежащие множеству 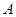, так и не принадлежащие множеству .
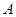Определение 5. Точка 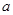называется точкой прикосновения множества 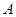, если в каждой ее окрестности существует хотя бы одна точка, принадлежащая множеству .
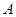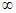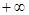Если точка прикосновения является одной из бесконечностей: 
, 
или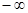 
, то она называется бесконечно удаленной точкой прикосновения.
Очевидно, что все элементы числового множества являются его точками прикосновения. Точками самого множества не исчерпываются, вообще говоря, все его точки прикосновения: могут существовать точки прикосновения и не принадлежащие ему. Например, точки 
и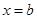 
являются точками прикосновения интервала 
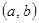и не содержатся в нем.
Определение 6. Точка 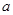называется предельной точкой множества 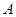, если в каждой ее проколотой окрестности существует хотя бы одна точка, принадлежащая множеству .
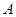Предельная точка всегда является точкой прикосновения, но не наоборот. Для множества рациональных чисел предельной является каждая точка R, так как в любом интервале вещественных чисел имеются рациональные числа.
Определение 7. Точка 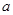называется изолированной точкой множества 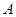, если у нее существует окрестность, не содержащая других точек множества 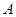, кроме самой точки .
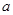Пример. Рассмотрим множество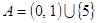 
. Для этого множества:
0, 1, 5 – граничные точк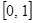и;
и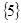 
– точки прикосновения;
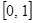– предельные точки;
5 – изолированная точка.
