1. В дифференцирующем звене выходная величина пропорциональна производной по времени от входной величины.
2. 
3. Примеры: спидометр в автомашине (вход – частота вращения колеса; выход – угол поворота стрелки спидометра), тахогенератор (вход – частота вращения; выход – напряжение на клеммах тахогенератора), индуктивное сопротивление при параллельном включении в электрическую цепь (вход – поданное напряжение; выход – скорость изменения напряжения).
4. 
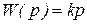
5. 
6. 
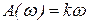
7. 
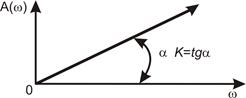
8.
9. 
5 Колебательное звено
1. В колебательном звене выходная величина описывается дифференциальным уравнением второго порядка с коэффициентом демпфирования от 0 до 1.
2. 
, где Т - постоянная времени колебательного звена; 
-коэффициент демпфирования.
3. Примеры: самый наглядный пример – это колебание маятника (рисунок 3.15). В положении 1 груз маятника имеет потенциальную энергию 
. В положении 2 груз маятника имеет кинетическую энергию движения 
, благодаря которой маятник переходит в положение 3 с потенциальной энергией 
и колебание маятника повторяется, но уже в другую сторону. Выходная величина этого звена- угол 
. Под действием трения груза маятника о воздух и в шарнирных соединениях энергия движения теряется и в конце концов маятник остановится в положении 2, где потенциальная и кинетическая энергия равна нулю (выходная величина 
).
Другой пример – груз подвешенный на пружине (рисунок 3.16). После подвешивания груз опускается вниз и растягивает пружину. При этом потенциальная энергия груза переходит в кинетическую энергию движения груза и затем в потенциальную энергию упругости растянутой пружины. Под действием силы упругости пружины груз поднимается вверх, сила упругости пружины уменьшается и становится меньше веса груза и груз снова опускается вниз. Таким образом, потенциальная энергия веса груза через кинетическую энергию движения переходит в потенциальную энергию упругости пружины. В данном случае движение прекращается, когда эти две потенциальные энергии уравновешиваются.Третий пример – электрический колебательный контур, (рисунок 3.17) содержащий активное сопротивление, индуктивность и емкость (или цепочка RCL). Напряжение, поданное на вход контура, преобразуется в электромагнитную энергию индуктивного сопротивления. Разряжаясь через конденсатор, энергия переходит в электростатическую энергию заряда пластин конденсатора. Эта энергия конденсатора разряжается, через индуктивность снова переходит в электромагнитную энергию индуктивного сопротивления и так далее. При таком переходе одной энергии (электромагнитной) в другую энергию (электростатическую) часть энергии теряется в активном сопротивлении (переходит в тепловую энергию нагрева сопротивления) и, в конце концов, становится равной нулю.
Вывод: физическая причина колебательности в колебательном звене в наличии в звене двух емкостей, способных запасать энергию и обмениваться этими запасами.
4. 
Определим корни характеристического полинома
При значении в пределах 
считается, что колебательное звено нормально – демпфированное. Определим корни характеристического полинома при 
.
или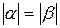 
При 
возможен переход одной энергии в другую, но не более 5 % от первоначальной.
При значении в пределах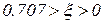 
считается, что колебательное звено слабо – демпфированное. При этом 
. Амплитуда выходного сигнала при 
больше, чем амплитуда входного сигнала.
При значении 
считается, что колебательное звено недемпфированное. Такое звено называется консервативное.
Амплитуда выходного сигнала при ω0 может неограниченно возрастать.
5. Частотная передаточная функция или амплитудно-фазовая характеристика
6. 
Для построения графика амплитудной характеристики определим ее значение при 
(рисунок 3.18)
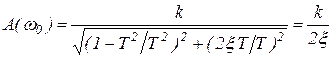
При 
0,707 
0,707k
При 0,25 2k
При 0,15 3,3k
При 0,10 5k
7. Фазовая характеристика
.
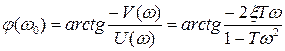При 
;
При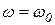 
;
При 
8.
9. 
,где 
; 
; 
;
где – вещественная часть корня характеристического уравнения;
– мнимая часть корня.
