Элементарные звенья системы управления
Любая система автоматического управления представляет собой определенное сочетание функциональных звеньев (задающее устройство, датчики, исполнительное устройство, усилители и т.д.).
Эти звенья могут иметь разную конструкцию и разный принцип действия. При анализе динамических свойств системы можно не рассматривать эти конструктивные особенности. Необходимо определить закон преобразования сигнала в каждом функциональном звене и в результате получить структурную схему системы. Обычно математическое описание преобразованного сигнала в функциональном звене сводится к дифференциальному уравнению первого или второго порядка. Поэтому передаточные функции этих звеньев также имеют первый или второй порядок. Коэффициенты, входящие в передаточную функцию, непосредственно связаны с конструктивными параметрами функциональных звеньев. Таким образом, полученная структурная схема разбивается на элементарные звенья, а затем по правилам структурных преобразований получают общую передаточную функцию системы или, другими словами, получают математическую модель системы в виде общей передаточной функции.
Элементарным звеном называется звено, описываемое дифференциальным уравнением не выше второго порядка.
Все элементарные звенья можно разделить на две группы: устойчивые или минимально-фазовые и неустойчивые или неминимально-фазовые.
Устойчивым звеном называется такое, все полюсы передаточной функции которого имеют отрицательные действительные числа или равные нулю.
Устойчивым звеном называется такое, переходная функция которого имеет установившееся значение или изменяющееся с постоянной скоростью.
Устойчивым или минимально-фазовым звеном называется такое, которое имеет минимальный фазовый сдвиг по сравнению с любым имеющим такую же амплитудную характеристику.
Если в разомкнутой системе есть хотя бы одно неустойчивое звено, то вся система неустойчивая или, другими словами, неработоспособная.
Для анализа динамических характеристик элементарных звеньев используют передаточную функцию
В зависимости от значения Т1, 
, Т2, 
, λ, μ, которые могут быть равны нулю или больше нуля, различают 16 вариантов элементарных звеньев.
Таблица 3.1 – Элементарные звенья
| № п/п | Наименование звена | Передаточная функция |
| Усилительное Устойчивое апериодическое Интегрирующее μ-порядка Дифференцирующее λ-порядка Дифференцирующее 1 рода Дифференцирующее 2 рода (0 < ξ1 < 1) Устойчивое колебательное (0 < ξ2 < 1) Консервативное (ξ2 = 0) Звено чистого запаздывания | 
| |
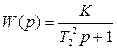
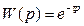
| Неустойчивое апериодическое Неустойчивое колебательное (0 < ξ2 < 1) Неустойчивое колебательное (0 < ξ2 < 1) Дифференцирующее 1 рода Дифференцирующее 2 рода (0 < ξ1 < 1) Дифференцирующее 2 рода (0 < ξ1 < 1) Вырожденное дифференцирующее 2 рода (ξ1 = 0) | 
|
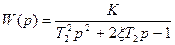
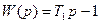
Обратите внимание. Первая группа элементарных звеньев имеет полюсы с отрицательными действительными числами или (для интегрирующего звена) полюс равен нулю. Полюс определяется путем приравнивания нижнего (характеристического) полинома к нулю. Эта же группа имеет нули передаточной функции с отрицательными действительными числами или равным нулю (для дифференцирующего звена). Соответственно эта группа имеет минимально – фазовую характеристику.
Вторая группа элементарных звеньев имеет положительные полюсы и положительные нули. Соответственно эта группа с неминимально – фазовой характеристикой.
