Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.
Рассмотрим один из методов, позволяющих проанализировать и обработать данные, полученные в результате эксперимента (таблица 1). Пусть в результате измерений получена таблица зависимости одной величины y от другой x.
Таблица 1
| X | X1 | X2 | … | Xn |
| F(x) | Y1 | Y2 | … | Yn |
Необходимо найти формулу y=f(x), выражающую таблично заданную зависимость аналитически. Применение интерполяции в данном случае нецелесообразно, т.к. значения yi в узлах получены экспериментально и поэтому являются сомнительными (в ходе эксперимента возникает неустранимая погрешность, обусловленная неточностью измерений). Кроме того, совпадение значений в узлах не означает совпадения характеров поведения исходной и интерполирующей функции. Поэтому необходимо найти такой метод подбора эмпирической формулы, который не только позволяет найти саму формулу, но и оценить погрешность подгонки.
Найдем функцию заданного вида
(1.1)
которая в точках x1,x2,…,xn принимает значения как можно более близкие к табличным значениям y1,y2,…,xn.
Практически вид приближающей функции можно определить визуально: по таблице 10.1 строится точечный график функции, а затем проводится кривая, по
возможности наилучшим образом отражающая характер расположения точек (рис.1.1).
Рис.1.1
По полученной кривой устанавливается вид приближающей функции (обычно из числа простых по виду аналитических функций: линейная, степенная,
экспоненциальная или показательная, логарифмическая, гипербола, дробно-рациональная и т.д.).
Заметим, что формула (1.1), называемая эмпирической формулой или уравнением регрессии y на x, позволяет находить значения функции f(x) для не табличных значений x, «сглаживая» результаты измерений величины y. Из рисунка 1.1 видно, что для каждого значения xi экспериментальное 
и расчетное 
значения различаются на некоторую величину 
, называемую абсолютной разностью. Потребовав, чтобы сумма квадратов абсолютных разностей для всех точек была минимальной, найдем оптимальные параметры функции f(x): если выполняется условие
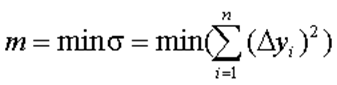(1.2)
где,
то считается, что функция f(x) подобрана наилучшим образом.
