1. Вектори  компланарні тоді і тільки тоді, коли їх мішаний добуток дорівнює нулю (
компланарні тоді і тільки тоді, коли їх мішаний добуток дорівнює нулю ( ), тобто
), тобто
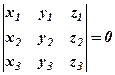 (3)
(3)
- умова компланарності трьох векторів.
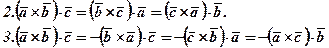
Властивості 2 і 3 випливають з того, що парна перестановка рядків визначника не змінює його знак, а непарна змінює на протилежний.
Об’єм піраміди, побудованої на векторах  дорівнює
дорівнює  об’єму відповідного паралелепіпеда, тобто
об’єму відповідного паралелепіпеда, тобто
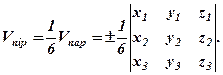
З двох знаків «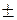 » вибираємо такий, щоб об’єм V був невідємним.
» вибираємо такий, щоб об’єм V був невідємним.
Приклад. Знайти об’єм піраміди з вершинами в точках А(0,-5,1), В(4,1.0), С(2,5,2) і S(3,-1,7).
Розв’язання. Знайдемо вектори 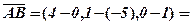

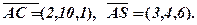
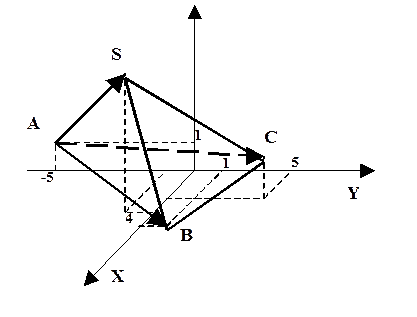
Обчислимо мішаний добуток векторів

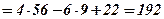 ,
,
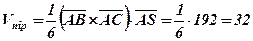 .
.
Приклади для самостійного розв’язання:
- Дано вектори
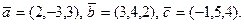 Необхідно: 1) Знайти спочатку векторний добуток
Необхідно: 1) Знайти спочатку векторний добуток  , а тоді скалярний
, а тоді скалярний  ; 2) обчислити
; 2) обчислити 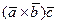 за формулою (2); 3) обчислити
за формулою (2); 3) обчислити 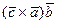 .
. - Знайти об’єм паралелепіпеда, побудованого на векторах

- Знайти об’єм піраміди побудованої на векторах
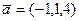 ,
,  ,
, 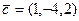 .
. - Обчислити об’єм піраміди з вершинами в точках А(2,-3,5), В(0,2,1), С(-2,-2,3) і D(3,2,4).
- Обчислити висоту AM піраміди АВСD, яка опущна з точки А на площину BCD, якщо вершини піраміди містяться в точках А(1,1,1), В(2,0,2), С(2,2,2), Д(3,4,-3).
- Встановити, чи компланарні вектори:
1) 
2) 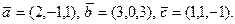
- З’ясувати, чи лежать точки А(3,0,0), В(1,1,8), С(2,1,6), D(3,1,4) в одній площині.
- Довести, що вектори
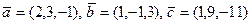 лінійно залежні та виразити лінійно
лінійно залежні та виразити лінійно 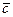 через
через  і
і  .
.
Відповіді: 1. 111. 2. 72. 3. 12. 4. 6. 5. 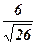 . 6. 1) так; 2) ні.
. 6. 1) так; 2) ні.
7. Так. 8.  .
.






