Во всякой реальной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы, т.е. затуханию колебаний.
Наиболее часто встречается случай, когда сила сопротивления пропорциональна скорости, т.е.
. 7.10
Уравнение второго закона Ньютона в этом случае будет иметь вид
.
Разделим это уравнение на 
, введем обозначения 
и тогда это уравнение примет вид:
. 7.10
Решение этого дифференциального уравнения в случае малого затухания 
можно представить в виде:
, 7.11
где 
.
Гармонический множитель 
в этом выражении ответственен за колебание, а множитель 
представляет собой амплитуду колебания. Следовательно, это решение можно рассматривать как гармоническое колебание, амплитуда которого с течением времени изменяется по экспоненциальному закону (рис. 46). Затухающее колебание происходит с частотой 
меньшей, чем частота собственных колебаний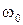 
.
Величина 
называется коэффициентом затухания.
Определим время 
в течении которого амплитуда колебания уменьшается в «е» раз. Если в момент времени 
амплитуда колебания 
, а в момент времени 
- 
, то
. 7.12
По условию 
, следовательно, 
, и
. 7.13
Коэффициент затухания численно равен обратному значению промежутка времени , в течение которого амплитуда колебания уменьшается в «е» раз.
Затухание колебаний принято характеризовать так называемым логарифмическим декрементом затухания – натуральным логарифмом отношения двух амплитуд колебания, отстоящих друг от друга на время равное периоду Т. (рис. 46).
. 7.14
Обозначим логарифмический декремент затухания буквой 
, т.е.
. 7.15
Так как то, для логарифмического декремента затухания получим 
.
Величина 
- число колебаний, которое должна совершить система, чтобы амплитуда колебания уменьшилась в «е» раз. Следовательно, логарифмический декремент затухания 
численно равен величине обратной числу колебаний, в течение которых амплитуда колебания уменьшается в «е» раз,
. 7.16
Для характеристики колебательной системы часто используют также величину
7.17
называемую добротностью системы.
Ранее мы показали, что энергия колеблющейся системы пропорциональна квадрату амплитуды. Поэтому в случае затухающих колебаний энергия системы будет изменяться по закону
. 7.18
Дифференцируя это уравнение по времени , найдем, что приращение энергии
.
Если затухание мало, то убыль энергии системы за один период 
. Отсюда
,
но 
и тогда
. 7.19
Из этого выражения следует, что при слабом затухании колебаний, добротность системы с точностью до множителя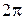 
равна отношению энергии, запасенной системой в данный момент времени, к убыли этой энергии в течение одного полного колебания.
