Рассмотрим колебания описываемые уравнением 
. Общее решение этого однородного дифференциального уравнения с постоянными коэффициентами ищется в виде
,
где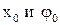 
- произвольные постоянные, обусловленные начальными условиями.
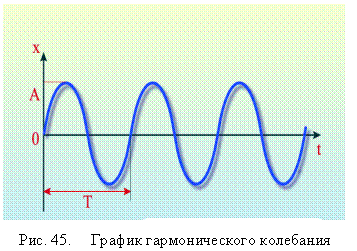
В том, что это соотношение удовлетворяет дифференциальному уравнению легко убедиться, подставив в него предполагаемую функцию и ее вторую производную по t,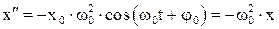 
. График гармонического колебания представлен на рисунке 45.
Величина наибольшего отклонения системы от положения равновесия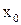 
называется амплитудой колебания. Величина 
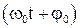называется фазой колебания, а 
- начальная фаза. С изменением начала отсчета времени будет изменяться и начальная фаза.
Периодом колебания называется промежуток времени в течение которого фаза колебания изменяется на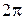 
, т.е. система совершает одно полное колебание, 
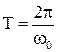. Тогда для:
пружинного маятника -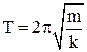 
, 7.4
физического маятника -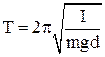 
, 7.5
математического маятника -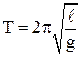 
. 7.6
Дифференцируя уравнение по времени можно найти выражения для скорости и ускорения тела при гармоническом колебании:
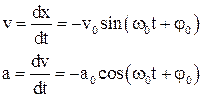. 7.7
При гармоническом колебании кинетическая энергия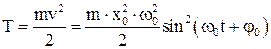 
, и потенциальная энергия 
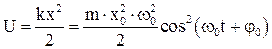также изменяются по гармоническому закону (рис. 45).
Квазиупругая сила является консервативной силой и поэтому полная механическая энергии колеблющейся системы остается величиной постоянной (рис. 45).
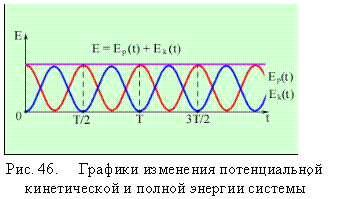
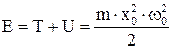. 7.8
Выясним теперь, как изменяется кинетическая и потенциальная энергия системы. Так как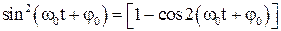 
и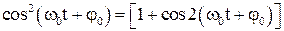 
получим:
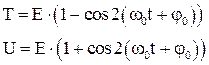, 7.9
т.е. кинетическая и потенциальная энергия изменяются с удвоенной частотой.
