| Вычисление неопределенного интеграла | |
| Интеграл с переменным верхним пределом Интегралы, содержащие квадратный трёхчлен Интегралы, сводящиеся к интегралам от рациональных функций Матрица Гессе | |
| Несобственные интегралы первого и второго рода | |
| Определение первообразной и её свойстваСвойства несобственных интегралов первого и второго рода | |
| Кратные интегралы | |
| Вычисление двойного и тройного интеграла Геометрические и физические приложения кратных интегралов | |
| Первообразная и производная | |
| Определение первообразной и её свойства Частные производные Производная сложной функции | |
| Формула замены переменного и интегрирование по частям в определённом интеграле | |
| Определенные, криволинейные и поверхностные интегралы | |
| Свойства криволинейного интеграла первого и второго рода Таблица изображений некоторых функций | |
| Функциональные и степенные ряды, сходимость ряда | |
| Критерий Коши необходимые и достаточные условия сходимости ряда Функциональные последовательности Разложение функций в степенные ряды Ряд Фурье для четных и нечетных функций | |
| Решение дифференциального уравнения | |
| Обыкновенные дифференциальные уравнения Дифференциальные уравнения первого порядка Уравнения с разделяющимися переменными Метод Лагранжа |
Определение. Трансцендентными называются аналитические функции, которые не являются алгебраическими.
Если аргументом показательной или тригонометрических функций является комплексное число, то определение этих функций, вводимое в элементарной алгебре теряет смысл.
Рассмотрим разложение в степенной ряд следующих функций:
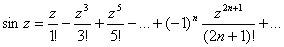
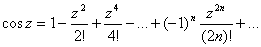
Функции ez, cosz, sinz связаны между собой формулой Эйлера Эта формула может быть очень легко получена сложением соотвествующих рядов.
Также справедливы равенства:
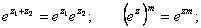
Для тригонометрических функций комплексного аргумента справедливы основные тригонометрические тождества (синус и косинус суммы, разности и т.д.), которые справедливы для функций действительного аргумента.
Определение. Гиперболическим синусом, косинусом, тангенсом и котангенсом называются соответственно функции:
Гиперболические функции могут быть выражены через тригонометрические:
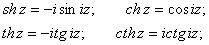
Гиперболические функции sh z и ch z имеют период 2pi, а функции th z и cth z – период pi.
Пример. Найти sin(1+2i).
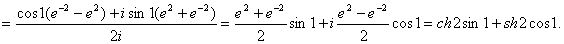
Определение. Логарифмическая функция комплексного аргумента определяется как функция, обратная показательной.
Если w = u + iv, то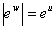 
и Arg ew = 
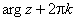= v.
Тогда eu = 
.
Итого: 
Для комплексного числа z = a + ib 
