Пусть в списке букв конечного алфавита А порядок букв зафиксирован, то есть всегда один и тот же, как, например, в русском и латинском алфавите. Тогда этот список определяет полное упорядочение букв, которое назовем отношением предшествования и обозначим «
»:
, если 
предшествует 
в списке букв.
На основе отношения предшествования букв, строится отношение предшествования слов, определяемое следующим образом.
Пусть даны слова 
и 
.
Тогда, 
тогда и только тогда, когда
1) 
, где (
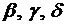- слова возможно непустые, 
- буквы);
2) 
, где 
- непустое слово.
Это отношение задает полное упорядочение множества всех конечных слов в алфавите А, которое является лексикографическим упорядочением слов.
Пример 5.1.
Отношение R «иметь одинаковый остаток от деления на 4» задано на множестве натуральных чисел N.
Построить матрицу бинарного отношения, определить свойства отношения. Является ли оно отношением эквивалентности? Порядка? Если R – отношение эквивалентности, то указать разбиение на классы эквивалентности и определить индекс разбиения. Если R – отношение порядка, то указать строгий порядок или не строгий, полный или не полный (почему?).
Решение.
Каждое натуральное число можно представить в виде суммы числа, кратного 4 и остатка от деления на 4.
Так 
. Здесь 0 – это целая часть от деления 1 на 4, 1 – остаток от деления 1 на 4.
Так 
. Здесь 3 – это целая часть от деления 12 на 4, 0 – остаток от деления 12 на 4. И так далее.
Всего различных остатков от деления на 4 – четыре: 0, 1, 2, 3.
Для построения матрицы бинарного отношения выпишем в заголовках строк и столбцов 9 элементов множества N.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 5 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 6 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 7 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 9 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
Определим свойства отношения.
1) Отношение рефлексивно, так как каждое натуральное число n имеет одинаковый остаток от деления на 4 с самим собой. То есть 
, 
, 
и так далее. Признаком этого является главная диагональ матрицы, заполненная единицами.
2) Отношение не антирефлексивно, так как рефлексивно. Одновременно рефлексивным и антирефлексивным отношение быть не может, так как эти два свойства взаимно исключают друг друга.
3) Отношение симметрично, так как если числа n 1и n 2 имеют одинаковые остатки от деления на 4, то числа n 2и n 1 тоже имеют одинаковые остатки от деления на 4. То есть 
; 
; 
и так далее.
Признаком симметричности является главная симметричная матрица бинарного отношения.
4) Отношение не является антисимметричным, так как оно симметрично. Одновременно симметричным и антисимметричным отношение быть не может, так как эти два свойства взаимно исключают друг друга.
5) Отношение является транзитивным, так как из того, что числа n 1и n 2 имеют одинаковые остатки от деления на 4 и n 2и n 3 имеют одинаковые остатки от деления на 4 следует, что n 1и n 3 тоже имеют одинаковые остатки от деления на 4. То есть 
; 
и так далее.
Таким образом, отношение R является рефлексивным, симметричным и транзитивным, следовательно, является отношением эквивалентности.
Известно, что отношение эквивалентности разбивает множество, на котором оно задано на классы.
Образуем первый класс. Возьмем любое натуральное число, например 1, и поместим его в класс С 1 . В этот же класс помещаем все натуральные числа имеющие тот же остаток от деления на 4, что и 1. Так как , 
, 
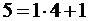и так далее. То есть С 1 = {1, 5, 9,…}.
Образуем второй класс. Возьмем любое натуральное число, не вошедшее в С 1, например 2, и поместим его в класс С 2 . В этот же класс помещаем все натуральные числа имеющие тот же остаток от деления на 4, что и 2. Так как 
, 
, 
и так далее. То есть С 2 = {2, 6, 10, …}.
Аналогично образуем третий и четвертый классы эквивалентности. С 3 = {3, 7, 11, …}, С 4 = {4, 8, 12, …}.
Количество классов эквивалентности – индекс разбиения – равен I = 4.
Пример 5.2.
На множестве чисел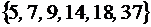 
задано отношение 
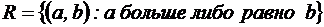. Построить матрицу бинарного отношения, определить свойства отношения. Является ли оно отношением эквивалентности? Порядка? Если R – отношение эквивалентности, то указать разбиение на классы эквивалентности и определить индекс разбиения. Если R – отношение порядка, то указать строгий порядок или не строгий, полный или не полный (почему?)
Решение.
Для построения матрицы бинарного отношения выпишем в заголовках строк и столбцов элементы данного множества.
| 5 | 7 | 9 | 14 | 18 | 37 | |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | 1 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 1 | 1 | 0 | 0 | 0 |
| 14 | 1 | 1 | 1 | 1 | 0 | 0 |
| 18 | 1 | 1 | 1 | 1 | 1 | 0 |
| 37 | 1 | 1 | 1 | 1 | 1 | 1 |
Определим свойства отношения.
1) Отношение рефлексивно, так как каждое натуральное число m из множества М больше или равно самому себе. То есть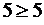 
, 
, 
и так далее. Признаком этого является главная диагональ матрицы, заполненная единицами.
2) Отношение не антирефлексивно, так как рефлексивно. Одновременно рефлексивным и антирефлексивным отношение быть не может, так как эти два свойства взаимно исключают друг друга.
3) Отношение не симметрично, так как из того, что 
не следует, что 
.
4) Отношение антисимметрично, так как если число 
, то число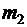 
не может быть больше или равно числа 
. Признаком антисимметричного отношения является нижнетреугольная (или верхнетреугольная) матрица бинарного отношения.
5) Отношение является транзитивным, так как для любых трех чисел множества М, таких что 
и 
следует, что 
. То есть 
; 
и так далее.
Таким образом, отношение R является рефлексивным, антисимметричным и транзитивным, следовательно, это отношение нестрогого порядка.
Любое отношение порядка может задавать либо полный, либо частичный порядок элементов множества М. Заметим, что отношение «больше либо равно» позволяет упорядочить любую пару различных элементов. То есть для любых двух чисел 
выполняется либо 
. Значит порядок полный. А именно: 
.
Пример 5.3.
Отношение R на множестве слов М = 
задано в виде:
Построить матрицу бинарного отношения, определить свойства отношения. Является ли оно отношением эквивалентности? Порядка? Если R – отношение эквивалентности, то указать разбиение на классы эквивалентности и определить индекс разбиения. Если R – отношение порядка, то указать строгий порядок или не строгий, полный или не полный (почему?).
Решение.
Для построения матрицы бинарного отношения выпишем в заголовках строк и столбцов элементы данного множества.
| abb | ba | ac | ca | bba | bbb | |
| abb | 0 | 1 | 0 | 1 | 1 | 1 |
| ba | 1 | 0 | 1 | 1 | 0 | 0 |
| ac | 0 | 1 | 0 | 1 | 1 | 1 |
| ca | 1 | 1 | 1 | 0 | 1 | 1 |
| bba | 1 | 0 | 1 | 1 | 0 | 0 |
| bbb | 1 | 0 | 1 | 1 | 0 | 0 |
Определим свойства отношения.
1) Отношение не рефлексивно, так как элемент abb не состоит с элементом abb в данном отношении R, то есть 
.
2) Отношение антирефлексивно, так как никакой элемент множества М, не состоит в данном отношении сам с собой (у всех одинаковых слов одинакова первая буква). Признаком этого является главная диагональ матрицы, заполненная нулями.
3) Отношение симметрично, так как если в слове X и Y различны первые буквы, то и в словах Y и X также различны первые буквы. Признаком этого является главная симметричная матрица бинарного отношения.
4) Отношение не является антисимметричным, так как оно симметрично. Одновременно симметричным и антисимметричным отношение быть не может, так как эти два свойства взаимно исключают друг друга.
5) Отношение не является транзитивным, так как из того, что слова bba и abb имеют разные первые буквы и, при этом, слова abb и bbb имеют разные первые буквы, то это не означает, что слова bba и bbb также имеют разные первые буквы.
То есть 
и 
.
Таким образом, отношение R является антирефлексивным, следовательно, не может быть отношением эквивалентности; не является транзитивным, значит, не может быть отношением порядка.
ГЛАВА 2. ТЕОРИЯ ГРАФОВ
