Для задания бинарных отношений можно использовать любые способы задания множеств (например, список пар, для которых данное отношение выполняется).
Бинарные отношения, определяемые на конечном множестве, обычно задаются списком пар элементов, бинарной матрицей.
Матрица бинарного отношения, заданного на множестве 
– это квадратная матрица С порядка n, в которой 
(где i – номер строки, j - номер столбца) определяется так:
Для любого множества М отношение Е, заданное единичной матрицей, в которой по главной диагонали стоят “1”, а остальные “0” – называется отношением равенства.
Свойства бинарных отношений
Отношение R на М называется рефлексивным, если для любого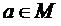 
выполняется 
. Главная диагональ матрицы такого отношения содержит только единицы.
Отношение R на М называется антирефлексивным, если ни для какого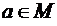 
не выполняется. Главная диагональ матрицы отношения содержит только нули.
Отношение R на М называется симметричным, если для любой пары 
из aRb следует bRa (иначе говоря, для любой пары отношение R выполняется в обе стороны или не выполняется вообще). Матрица симметричного отношения – симметрична относительно главной диагонали: 
для всех i, j, то есть 
Отношение R на М называется антисимметричным, если из того, что выполняется aRb и bRa следует, что a = b (то есть ни для каких различных элементов множества М отношение R не выполняется в обе стороны). Матрица антисимметричного отношения не имеет ни одного симметричного относительно главной диагонали единичного элемента.
Отношение R на М называется транзитивным, если для любых a, b, c из множества М из того, что выполняется aRb и bRc следует, что aRc.
Отношение эквивалентности
Отношение R на М называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из Е (то есть любой единицы на диагонали матрицы Е) оно перестает быть рефлексивным и, следовательно, уже не является эквивалентным.
Пусть на множестве М задано отношение эквивалентности R. Осуществим построение классов эквивалентности, на которые разбивается множество М этим отношением.
Выберем элемент 
и образуем класс (подмножество М) 
, состоящий из 
и всех элементов, эквивалентных .
Затем выберем элемент 
, и образуем класс 
, состоящий из 
и всех элементов, эквивалентных и так далее.
Получится система классов 
(возможно бесконечная) такая, что любой элемент из М входит хотя бы в один класс, то есть
.
Эта система обладает свойствами:
1) она образует разбиение, то есть классы попарно не пересекаются;
2) любые два элемента из одного класса эквивалентны;
3) любые два элемента из разных классов неэквивалентны.
Мощность системы классов эквивалентности называется индексом разбиения.
Совокупность классов эквивалентности, на которые разбивается множество М по отношению эквивалентности R, называется фактор-множеством множества М по отношению R. Тогда классы эквивалентности – это элементы фактор-множества, а индекс разбиения – мощность фактор-множества.
С другой стороны, любое разбиение М на классы определяет некоторое отношение эквивалентности.
Отношение порядка
Отношение называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично, транзитивно.
Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично, транзитивно.
Оба типа таких отношений называются отношениями порядка.
Элементы a и b сравнимы по отношению порядка R, если выполняется aRb или bRa.
Множество М, на котором задано отношение порядка, называется полностью упорядоченным, если любые два элемента М сравнимы. Иначе говорят, обладает свойством полноты.
Множество М, на котором задано отношение порядка, называется частично упорядоченным, если не любые два элемента М сравнимы.
