Пусть V – множество вершин, а Е – множество ребер. Графом G называется пара объектов (V, E) между которыми задано отношение инцидентности:
Г: е → (v, w),
где вершина v и ребро eинцидентны друг другу, если вершина является для этого ребра концевой точкой.
Вершины v ' и v " называются смежными, если существует ребро, соединяющее их, то есть они инцидентны одному и тому же ребру.
Ребра e ' и e " называются смежными, если они имеют, по крайней мере, одну общую вершину (инцидентны одной вершине).
Граф, содержащий направленные ребра (дуги) с началом v ' и концом v ", называется ориентированнымграфом (орграфом). Для орграфа
.
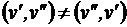Граф, содержащий ненаправленные ребра с конами v ' и v ", называется неориентированнымграфом (н-графом). Для н-графа
.
Рис.6.1 Неориентированное ребро (a, b)
Рис.6.2 Ориентированное ребро (a, b)
Ребро, концевые вершины которого совпадают, называется петлей.
Рис.6.3. Неориентированная петля
Рис.6.4. Ориентированная петля
Ребра (дуги), имеющие одинаковые начало и конец, называются параллельными или кратными.
Рис.6.5 Кратные неориентированные ребра
Рис. 6.6. Кратные ориентированные ребра
Ребра орграфа, соединяющие одну и туже пару вершин в разных направлениях называются симметричными или противоположно направленными.
Рис. 6.7. Симметричные ребра
Способы задания графа
Задать граф – значит описать множества его вершин и ребер, а также отношение инцидентности.
Для описания вершин и ребер достаточно их занумеровать.
Пусть 
вершины графа; 
ребра графа G.
Отношение инцидентности задается:
а) матрицей инцидентности 
размера 
(строкам соответствуют ребра, столбцам – вершины графа), в которой
для н-графа
для ор-графа
б) списком ребер графа, в котором каждая строка соответствует ребру и в ней записаны номера вершин графа, инцидентных этому ребру. Для н-графа порядок вершин в строке произволен, для ор-графа первым стоит номер вершины – начала ребра.
в) матрицей смежности 
размера 
, столбцам и строкам которой соответствуют вершины графа. Для н-графа 
равно количеству ребер, инцидентных i -й и j -й вершинам, для ор-графа – равно количеству ребер с началом в i -й и концом в j -й вершине.
г) рисунком или геометрической интерпретацией, когда вершинам сопоставть точки плоскости, ребрам – линии на плоскости, причем, линия соединяет только те точки, которые соответствуют вершинам, инцидентным данной линии-ребру.
Граф для которого возможна геометрическая интерпретация на плоскости, называется планарным.
Вид матриц и списка ребер зависит от нумерации вершин и ребер графа. Граф считается полностью заданным, если нумерация его вершин зафиксирована.
Графы, отличающиеся только нумерацией вершин, называются изоморфными.
