Образом множестваС Î пр 1 G называется объединение образов всех элементов С. Прообразом множестваD Î пр 2 G называется объединение прообразов всех элементов D.
Соответствие G называется функциональным (однозначным) соответствием, если образом любого элемента из пр 1 G является единственный элемент из пр 2 G. Иначе говорят, соответствие G обладает свойством единственности образа.
Соответствие G называется инъективным соответствием, если прообразом любого элемента из пр 2 G является единственный элемент из пр 1 G. Иначе говорят, соответствие G обладает свойством единственности прообраза.
Соответствие G является функцией f типа 
, если оно функционально. Обозначение функции: 
.
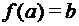Соответствие G является отображением множества А в множество В, если оно функционально и полностью определено.
Отображение 
будет отображением А в В, если G – не сюрьективно.
Отображение будет отображением А на В, если G – сюрьективно.
Соответствие G является взаимно однозначным, если оно: 1) всюду определено; 2) сюрьективно; 3) функционально; 4) инъективно.
Преобразованием множества А называется отображение типа 
.
Функция типа 
называется n- местной функцией. Это обозначается: 
.
Соответствие 
называется обратным к соответствию 
, если Н таково, что 
.
Можно обозначить обратное соответствие 
.
Если соответствие, обратное к функции 
является функциональным, то оно называется функцией, обратной к f. Обозначим обратную функцию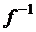 
.
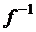Пусть дана функция . Соответствие является функцией тогда и только тогда, когда f инъективна, и 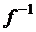является отображением тогда и только тогда, когда f инъективна и сюрьективна (то есть биективна).
Утверждение:
Для функции существует обратная функция 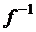тогда и только тогда, когда f является взаимно однозначным соответствием между своей областью определения и областью значений.
Пусть даны функции и 
.
Функция 
называется композицией функций f и g, если 
. Это обозначение 
). Часто говорят, что h получена подстановкой f в g.
Для многоместных функций 
и 
возможны различные варианты подстановки f в g, задающие функции различных типов. Например, при 
и 
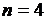функция
имеет 6 аргументов и тип 
.
Для множества многоместных функций типа 
возможны любые подстановки функций друг в друга, а также любые переименования аргументов. Например, переименование 
в 
из функции 
четырёх аргументов порождает функцию трёх аргументов: 
.
Функция, полученная из функций 
некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией функций . Выражение, задающее эту суперпозицию и содержащее функциональные знаки, скобки и символы аргументов, называется формулой.
Пример 4.1.
Соответствие G = 
является подмножеством прямого произведения множеств 
и 
.
Определить свойства соответствия. Является ли оно функцией? Отображением? Почему? Является ли оно взаимно однозначным?
Решение.
На рисунке 4.1 приведена схема соответствия G.
Множества А и В обозначены кругами Эйлера. Внутри каждого множества указаны все его элементы. Если элемент множества А связан с элементом множества В соответствием G, то на рисунке эти элементы связаны стрелкой.
Рис. 4.1 Соответствие
Найдем область определения соответствия G – множество пр 1 G Í A. Так как соответствие – это совокупность векторов длины 2, то его проекция на 1 ось – это множество всех первых координат этих векторов.
В нашем случае, пр 1 G Í = {1, 2}. Здесь всего два элемента, так как во 2-ой и 3-ей паре множества G одинаковые первые координаты. Откуда можно сделать вывод, что 
. Согласно определению, это означает, что соответствие G является частично определенным. Действительно, так как пары с первой координатой 3 в соответствии G нет, значит G определено не на всех элементах множества А, то есть оно определено не полностью (частично).
Найдем область значений соответствия G – множество пр 2 G Í В. Это множество всех вторых координат этих пар, входящих в соответствие G.
В нашем случае, пр 2 G = { a, b, c }. Откуда можно сделать вывод, что 
. Согласно определению, это означает, что соответствие G является сюрьективным.
Найдем образ каждого элемента области определения.
G (1) = { a }, так как в множестве G имеется единственная пара с первой координатой 1. Это пара (1, а). То есть элементу 1 из области определения соответствует единственный элемент а из области значений. На рисунке 4.1 видно, что из 1 идет единственная стрелка в элемент а.
G (2) = { b, c }, так как в множестве G имеется две пары с первой координатой 2. Это пары (2, b) и (2, c). То есть элементу 2 из области определения соответствует два элемента b и c из области значений. На рисунке 4.1 видно, что из 2 идет две стрелки в b и в c.
Образ элемента 3 не ищем, так как он не принадлежит области определения.
Отсюда можно сделать вывод: так как единственности образа нет, то соответствие G не является функциональным.
Найдем прообраз каждого элемента области значений.
G - 1(а) = {1}, так как в множестве G имеется единственная пара со второй координатой а. Это пара (1, а). То есть элемент а из области значений соответствует единственному элементу 1из области определений. На рисунке 4.1 видно, что в а идет единственная стрелка из элемента 1.
G - 1(b) = {2}, так как в множестве G имеется единственная пара со второй координатой b. Это пара (2, b). То есть элемент b из области значений соответствует единственному элементу 2из области определений. На рисунке 4.1 видно, что в b идет единственная стрелка из элемента 2.
G - 1(c) = {2}, так как в множестве G имеется единственная пара со второй координатой c. Это пара (2, c). То есть элемент c из области значений соответствует единственному элементу 2из области определений. На рисунке 4.1 видно, что в c идет единственная стрелка из элемента 2.
Отсюда можно сделать вывод: так как единственности прообраза есть, то соответствие G является инъективным.
Таким образом, соответствие G обладает свойствами:
1) не полностью (частично) определено,
2) сюрьективно,
3) не функционально,
4) инъективно.
Ответим далее на вопросы.
Соответствие G не является функцией, так как оно не функционально.
Соответствие G не является отображением, так как оно не функционально и не полностью определено.
Соответствие G не является взаимно однозначным, так как оно сюрьективно и инъективно, но не функционально и не полностью определено.
Пример 4.2.
Соответствие H = 
является подмножеством прямого произведения множеств 
и 
.
Определить свойства соответствия. Является ли оно ункцией? Отображением? Почему? Является ли оно взаимно однозначным?
Решение.
На рисунке 4.2 приведена схема соответствия Н.
Рис. 4.2 Соответствие 
Найдем область определения соответствия H – множество пр 1 H Í M. Так как соответствие – это совокупность векторов длины 2, то его проекция на 1 ось – это множество всех первых координат этих векторов.
В нашем случае, пр 1 H = { k, p, q }. Откуда можно сделать вывод, что 
. Согласно определению, это означает, что соответствие H является полностью определенным.
Найдем область значений соответствия H – множество пр 2 H Í N. Это множество всех вторых координат этих пар, входящих в соответствие H.
В нашем случае, пр 2 H = {2, 4}. Здесь всего два элемента, так как во 1-ой и 3-ей паре множества H одинаковые вторые координаты. Откуда можно сделать вывод, что 
. Согласно определению, это означает, что соответствие H является не сюрьективным.
Найдем образ каждого элемента области определения.
H (k) = {2}, так как в множестве H имеется единственная пара с первой координатой k. Это пара (k, 2). То есть элементу k из области определения соответствует единственный элемент 2из области значений. На рисунке 4.2 видно, что из k идет единственная стрелка в элемент 2.
H (p) = {4}, так как в множестве H имеется единственная пара с первой координатой p. Это пара (p, 4). То есть элементу p из области определения соответствует единственный элемент 4из области значений. На рисунке 4.2 видно, что из p идет единственная стрелка в элемент 4.
H (q) = {2}, так как в множестве H имеется единственная пара с первой координатой q. Это пара (q, 2). То есть элементу q из области определения соответствует единственный элемент 2из области значений. На рисунке 4.2 видно, что из q идет единственная стрелка в элемент 2.
Отсюда можно сделать вывод: так как есть единственность образа, то соответствие H является функциональным.
Найдем прообраз каждого элемента области значений.
H - 1(2) = { k, q }, так как в множестве H имеется две пары со второй координатой 2. Это пары (k, 2) и (q, 2). То есть элемент 2 из области значений соответствует двум различным элементам из области определений. На рисунке 4.2 видно, что в 2 идет две стрелки из элементов k и q.
H - 1(4) = { p }, так как в множестве H имеется единственная пара со второй координатой 4. Это пара (p, 4). То есть элемент 4 из области значений соответствует единственному элементу p из области определений. На рисунке 4.2 видно, что в 4 идет единственная стрелка из элемента p.
Прообраз элемента 6 из множества N не ищем, так как он не принадлежит области значений.
Отсюда можно сделать вывод: так как единственности прообраза есть, то соответствие H не является инъективным.
Таким образом, соответствие H обладает свойствами:
1) полностью определено,
2) не сюрьективно,
3) функционально,
4) не инъективно.
Ответим на вопросы.
Соответствие H является функцией, так как оно функционально.
Соответствие H является отображением, так как оно функционально и полностью определено.
Соответствие H является отображением M в N, так как оно не сюрьективно.
Соответствие H не является взаимно однозначным, так как оно полностью определено и функционально, но несюрьективно и не инъективно,
Тема 5. Отношения
Подмножество 
называется n – местным отношением [2, 3] на множестве М. Говорят, что 
находится в отношении R, если 
.
Одноместное отношение – это просто подмножество М. Такие отношения называют признаками: элемент а – обладает признаком R, если 
и 
.
Свойства одноместных отношений это свойства подмножеств М, поэтому для случая n = 1 термин “отношение” употребляется редко.
Примером трехместного (тернарного) отношения является множество троек нападающих в хоккейной команде. Любой из нападающих находится в этом отношении со всеми теми игроками, с которыми он играет в одной тройке (один нападающий может, вообще говоря, участвовать более, чем в одной тройке).
При n = 2 – отношения называются двуместными или “бинарными”. Если a, b находятся в отношении R, это записывается aRb.
