Проекцией вектора 
на оси с номерами 
называется вектор 
длины k (обозначение 
).
Пусть V – множество векторов одинаковой длины.
Проекцией множества векторовV на i -ось называется множество проекций всех векторов из V на i -ось:
.
Проекция множества векторов V на оси с номерами :
.
Полезно помнить следующее:
- проекция вектора на одну ось – это вектор из одной координаты (скаляр),
- проекция вектора на две оси – вектор из двух координат,
- проекция вектора на три оси – вектор из трех координат, и так далее;
- проекция множества векторов на одну ось – это множество векторов из одной координаты (множество скаляров),
- проекция множества векторов на две оси – множество векторов из двух координат,
- проекция множества векторов на три оси – множество векторов из трех координат, и так далее.
Пример 2.2.
1) Проекция точки декартовой плоскости на 1-ю ось – ее абсцисса, на 2-ю ось – ее ордината.
2) Дано множество векторов
.
Тогда
– это вектор из одной координаты вектора 
, а именно, первой координаты;
– это вектор из одной координаты вектора 
, а именно, третьей;
– это вектор из одной координаты вектора 
, а именно, второй;
– это вектор из двух координат вектора , а именно первой и второй;
– это вектор из двух координат вектора 
, а именно второй и третьей;
– это вектор из двух координат вектора , а именно первой и третьей;
– это множество векторов, составленных из первых координат элементов V. Они все различны, поэтому 
;
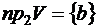– это множество векторов, составленных из вторых координат элементов V. Они все одинаковы, поэтому 
;
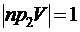– это множество векторов, составленных из третьих координат элементов V. Две из трех одинаковы, поэтому 
;
– это множество векторов, составленных из первых и вторых координат векторов множества V. Все проекции различны, поэтому 
;
– это множество векторов, составленных из вторых и третьих координат векторов множества V. Две их трех проекций одинаковы, поэтому 
;
– это множество векторов, составленных из первых и вторых координат векторов множества V. Все проекции различны, поэтому 
.
3) 
. Чему равна 
? Ее найти нельзя, так как заданное множество V – множество векторов разной длины, в отношении которых никаких определений не было сделано.
Тема 3. Комбинаторика
Одно из основных правил комбинаторики – правило суммы [1]. Его классическая формулировка имеет вид: если элемент 
можно выбрать k способами, а элемент 
можно выбрать m способами, тогда или можно выбрать k + m способами. Например, если в вазе 5 яблок и 6 груш, то 1 фрукт (яблоко или грушу) можно выбрать 5 + 6 = 11 способами.
Современная формулировка правила суммы известна как теорема о мощности объединения множеств: мощность объединения двух множеств равно сумме мощностей первого и второго множества, за вычетом мощности их пересечения:
. (3.1)
Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный классической формулировке:
. (3.2)
Для трех множеств теорема имеет следующий вид:
(3.3)
Пример 3.1. Из 35 учащихся класс по итогам года имели «5» по математике – 14 человек; по физике – 15 человек; по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек.
1) Сколько человек имеют «5» по указанным предметам?
2) Сколько человек не имеет «5» по указанным предметам?
3) Имеет «5» только по математике?
4) Имеет «5» только по двум предметам?
Решение.
Введем обозначения. Обозначим буквой U множество всех учеников класса, буквой М множество учеников, имеющих «5» по математике, буквой Ф – имеющих «5» по физике, Х – имеющих «5» по химии. Тогда, согласно условию,
1) На рисунке 3.1 приведено множество, состоящее из учеников, имеющих «5» хотя бы по одному из указанных предметов.
Рис. 3.1. Множество учеников,
имеющих «5» хотя бы по одному предмету
Очевидно, что это объединение множеств М, Ф и Х. Для нахождения количества элементов объединения воспользуемся формулой (3.3).
2) На рисунке 3.2 приведено множество, состоящее из учеников, не имеющих «5» ни по одному из указанных предметов. Обозначим его буквой Н.
Очевидно, что это разность между универсальным множеством U и объединением множеств М, Ф и Х. Для нахождения количества элементов множества Н (3.2).
Рис. 3.2. Множество учеников, не имеющих «5»
по указанным предметам
3) На рисунке 3.3 приведено множество, состоящее из учеников, имеющих «5» только по математике. Обозначим его буквами ТМ.
Рис. 3.3. Множество учеников, имеющих «5»
только по математике
Очевидно, что это разность между множеством М и множествами ТМФ – имеющих «5» только по математике и физике, ТМХ – имеющих «5» только по математике и химии, и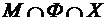 
.
Тогда
(3.4)
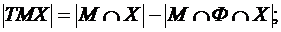(3.5)
4) На рисунке 3.4 приведено множество, состоящее из учеников, имеющих «5» только по двум предметам. Обозначим его Т 2. Очевидно, что Т 2 является суммой трех непересекающихся множеств ТМФ, ТМХ, ТФХ. Используя (3.4), (3.5) и то, что
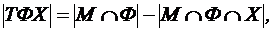
получим:
Рис. 3.4. Множество учеников, имеющих «5»
только по двум предметам
Тогда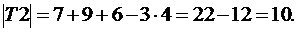 
Другое основное правило комбинаторики – правило произведения. Его классическая формулировка имеет вид: если элемент можно выбрать k способами, а элемент можно выбрать m способами, тогда и можно выбрать km способами. Например, если на гору ведут 2 дороги, а с горы – 3 дороги, то путь через перевал (дорогу на гору и дорогу с горы) можно выбрать 
способами.
Современная формулировка правила произведения известна как теорема о мощности прямого произведения множеств: количество элементов произведения двух множеств равно произведению количества элементов в первом и во втором множестве:
. (3.6)
Правило произведения можно применять для любого количества конечных множеств.
Пример 3.2.
1) Сколько четырехзначных чисел можно составить из цифр множества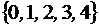 
? 2) в скольких из них только одна «2»?
Решение.
1) Четырехзначное число – это вектор длины 4, первая координата которого не может равняться «0».
Значит, все четырехзначные числа составляют множество 
Здесь 
цифры, претендующие на первое место числа, 
цифры, претендующие на второе место, и так далее.
Так как на первом месте не может стоять «0» значит, на него претендуют цифры «1», «2», «3», «4». То есть 
На втором месте может стоять любая цифра из списка «0», «1», «2», «3», «4». То есть 
Аналогично, на третьем и четвертом местах могут стоять любые цифры, значит 
Тогда по правилу произведения:
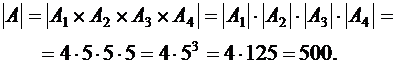
2) Пусть искомое множество чисел – В.
Пусть 
подмножество его элементов, где «2» стоит на первом месте. Здесь 
цифры, претендующие на первое место. Это только «2». Таким образом, 
На каждом из оставшихся мест не может быть «2», значит список претендентов: «0», «1», «3», «4». Откуда, 
Значит, таких чисел будет:
Пусть теперь «2» стоит на втором месте. Тогда претендентов на первое место – 3 («1», «3», «4»), на второе место – 1 (только «2»), на третье место – 4 («0», «1», «3», «4») и на четвертое место – те же 4 элемента. В итоге таких чисел 
Если «2» стоит на третьем месте, то, по аналогии, их тоже 48, если на последнем – 48. То есть 48 надо умножить на число способов выбрать место под «2» среди второго, третьего и четвертого, то есть на 3.
Таким образом, искомое количество чисел найдется по формуле:
Замечание: Факториалом натурального числа n называется функция, находимая по формуле:
Основные свойства факториала:
1) 
; 2) 
.
Из правила произведения выводятся различные комбинаторные формулы (комбинаторные числа). Перечислим основные из них.
Число размещений без повторений из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k различными координатами.
Число размещений без повторений находится по формуле:
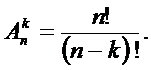(3.7)
Пример 3.3.
Сколькими способами можно построить 3-буквенное слово из букв множества 
так, что бы всебуквы в слове были различны?
Решение. В данном случае составляется вектор (слово) из трех различных букв (k = 3), причем буквы выбираются из множества с пятью различными элементами (n = 5). Количество таких слов (3.7) равно числу размещений без повторений из 5 по 3.
Число размещений с повторениями из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k координатами, среди которых могут быть одинаковые.
Число размещений с повторениями находится по формуле:
. (3.8)
Пример 3.4.
Человек забыл последние три цифры номера телефона. Сколько вариантов номеров он может перебрать?
Решение.
Здесь будет столько номеров, сколько можно составить векторов длины 3 (k = 3) с любыми цифрами из множества с десятью цифрами 
(n = 10). Тогда по формуле (3.8) получим:
.
Число перестановок без повторений из n элементов – это число способов, сколькими можно расположить на n различных местах n различных элементов.
Число перестановок без повторений находится по формуле:
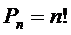. (3.9)
Пример 3.5.
1) Сколькими способами можно расставить на книжной полке 5 различных книг?
2) В скольких случаях две определенные книги А и В окажутся рядом?
Решение.
1) Согласно определению числа перестановок без повторений, 5 книг на 5 местах можно расставить 5! различными способами. Значит общее число расстановок (перестановок) найдется по формуле (3.9):
.
2) Пусть множество А составляют такие расстановки книг, где две определенные книги окажутся рядом. Для нахождения количества способов совершить такие расстановки, надо воспользоваться замечанием.
Замечание:
, (3.10)
где х – число способов выбратьнужные места; у – число способов расположить на них нужные элементы; z – число способов расположитьостальные элементы на оставшихся местах.
На рисунке 3.5 приведена схема расстановки книг. В нашем случае нужные места – это два места рядом. Выбор двух мест рядом из 5 мест производится путем перебора. На рисунке видно, что это пары мест под номерами 12, 23, 34, 45. В итоге этих пар – 4.
Таким образом, в формуле (3.10) х = 4.
Рис. 3.5. Схема выбора нужных мест
На рисунке 3.6 показано, как на двух выбранных местах можно расставить две 2 книги А и В.
Вообще говоря, то, что для каждой пары выбранных мест имеется ровно два варианта расстановки книг А и В, можно было найти по формуле (3.9). Действительно, 2 элемента на 2 местах можно расставить 2! различными способами. Таким образом, в формуле (3.10) y = 2! = 2.
На рисунке 3.7 показано, как на оставшихся 3 местах можно расставить остальные три книги. При этом, положение книг А и В уже зафиксировано.
Рис. 3.6. Схема расстановки
нужных элементов на выбранных местах
Рис. 3.7. Схема расстановки
остальных элементов на оставшихся местах
Заметим, что количество вариантов расстановки оставшихся 3 книг на оставшихся 3 местах можно было найти по формуле (3.9). Действительно, 3 элемента на 3 местах можно расставить 3! различными способами. Таким образом, в формуле (3.10) z = 3! = 6.
В итоге, искомое количество расстановок равно:
.
Число перестановок с повторениями из n элементов, среди которых 
одинаковых, 
одинаковых, …, 
одинаковых, причем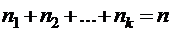 
, находится по формуле:
. (3.11)
Пример 3.6. Сколько различных слов моно получить, переставляя карточки разрезной азбуки с буквами слова «мама»?
Решение.
Известно, чточетыре цифры 1, 2, 3, 4 можно переставлять друг с другом 4! различными способами. В слове «мама» – 4 буквы. Но перестановок из этих букв можно составить не 4! = 24, а всего лишь 6:
мама, маам, ммаа, амам, аамм, амма.
Чтобы понять, как это случилось, поставим в соответствие цифрам 1 и 2 букву «м», а цифрам 3 и 4 – букву «а». Тогда, например, перестановке цифр 1234 – соответствует слово «ммаа», а перестановке 1324 – слово «мама».
Но слово «ммаа» соответствует не только перестановке 1234, но и перестановки 2134, 1243, 2143. Если цифры 1 и 2 меняются местами, то в соответствующем слове меняются местами две буквы «м», следовательно, само слово остается неизменным. Таким образом, среди 24 перестановок четырех указанных букв будут одинаковыми 2! тех, которые отличаются лишь сменой мест букв «м», а также 2! тех, которые отличаются лишь переменой букв «а».
И тогда это число различных слов будет меньше 4! в 2!2! раза:
.
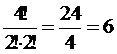Пример 3.7.
1) Сколькими способами можно получить слово «обороноспособность», переставляя местами карточки разрезной азбуки, с буквами О, Б, О, Р, О, Н, О, С, П, О, С, О, Б, Н, О, С, Т, Ь? 2) Сколько различных слов можно составить переставляя карточки разрезной азбуки с буквами О, Б, О, Р, О, Н, О, С, П, О, С, О, Б, Н,
О, С, Т, Ь?
Решение.
1) Чтобы ответить на 1 вопрос, воспользуемся правилом произведения. Для получения слова «обороноспособность» при перестановке местами карточек разрезной азбуки с указанными буквами, надо выяснить, сколько карточек претендует на каждое из 18 мест, с тем, чтобы в итоге получилось нужное слово. Заметим, что букв «о» в слове 
, букв «б» – 
, букв «р» – 
, букв «н» – 
, букв «с» – 
, букв «п» – 
, букв «т» – 
, букв «ь» – 
.
Так на первое место – 7 претендентов, так как первую букву слова «обороноспособность» (букву «о») можно выбрать 7 способами. На втором месте – буква «б». Карточек с буквой «б» 2 штуки. Значит, претендентов на второе место – 2. На третье место, где тоже стоит буква «о», уже только 6 претендентов, так как одна из 7 карточек с буквой «о» использована.
Таким образом, количество элементов множества А – всех перестановок 18 карточек, приводящих к слову «обороноспособность» надеется как произведение:
.
2) Чтобы определить, сколько различных слов можно составить переставляя карточки разрезной азбуки с буквами О, Б, О, Р, О, Н, О, С, П, О, С, О, Б, Н, О, С, Т, Ь, нужно восполь-зоваться формулой (3.11). Здесь общее число элементов n = 18. Причем эти элементы делятся на 8 групп с одинаковыми элементами, количества которых:
, , 
, , 
, 
, , 
;
.
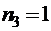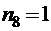Тогда по формуле (11) искомое количество различных слов будет равно:
Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k штук без учета порядка.
Формула для нахождения числа сочетаний без повторений имеет вид:
. (3.12)
Свойства:
1) 
; 2) 
;
3) 
; 4) 
.
5) 
;
6) 
; 7) 
.
С помощью числа сочетаний без повторений чаще всего решают урновую задачу – задачу, в которой производится неупорядоченный выбор сразу нескольких элементов из заданной совокупности.
Пример 3.8. В урне 7 шаров. Из них 3 белых и 4 черных шара. Наугад выбирают 3 шара. 1) Сколькими способами это можно сделать? 2) В скольких случаях среди них будет: А) один белый; В) один черный; С) хотя бы один белый шар?
Решение. Построим схему урновой задачи (см. рис. 3.8).
Рис.3.8. Схема урновой задачи
1) Общее число способов выбрать 3 элемента их 7 без учета порядка найдется как число сочетаний без повторений из 7 по 3по формуле (3.12).
То же самое можно было найти, воспользовавшись свойством 7.
2) Для нахождения числа способов выбрать такие три шара, чтобы среди них был 1 белый и 2 черных, надо найти отдельно число способов выбрать 1 белый шар из 3 белых и число способов выбрать 2 черных шара из 4 черных, и перемножить их согласно правилу произведения.
Здесь были использованы свойства 3 и 6.
Для нахождения числа способов выбрать такие три шара, чтобы среди них был 2 белых и 1 черный, надо найти отдельно число способов выбрать 2 белых шара из 3 белых и число способов выбрать 1 черный шара из 4 черных, и перемножить их.
Здесь были использованы свойства 4 и 3.
Для нахождения числа способов выбрать такие три шара, чтобы среди них был хотя бы 1 белый, воспользуемся подходом «от обратного». Для этого найдем количество способов, выбора таких трех шаров, где нет белых, и вычтем это число из общего количества способов выбрать три шара.
Среди 3 белых шаров берем 0 белых, среди 4 черных – 3 черных.
Здесь были использованы свойства 1 и 4.
Тогда искомое число равно:
Тема 4. Соответствия
Соответствием [4, 5] множеств А и В называется подмножество G такое, что 
. Если 
, то говорят, что «b соответствует a при соответствии G».
Область определения соответствия G – множество пр 1 G Í A.
Область значений соответствия G – множество пр 2G Í B.
Соответствие G называется всюду (полностью) определенным – если пр 1 G = А (в противном случае – частично определенное соответствие).
Соответствие G называется сюрьективным, если пр 2 G = B.
