ДИСКРЕТНАЯ МАТЕМАТИКА
Часть 1
Учебно-методическое пособие
Кемерово
2018
© С. Г. Гутова, 2018
© Кемеровский государственный
университет, 2018
ISBN 978-5-8353-1686-1
Об издании – 1, 2, 3
ББК В19я73-5
УДК 519.6(075.8)
Г 89
Издается по решению редакционно-издательского совета
Кемеровского государственного университета
Составитель:
Гутова Светлана Геннадьевна – кандидат технических наук, доцент кафедры прикладной математики
Г 89Гутова, С. Г. Дискретная математика. Ч. 1: электронное учебно-методическое пособие [Электронный ресурс]: / С. Г. Гутова; КемГУ. – Электрон. дан. (1 Мб). – Кемерово: КемГУ, 2018. – 1 электрон. опт. диск (СD-ROM). – Систем. требования: Intel Pentium (или аналогичный процессор других производителей), 500 МГц; 512 Мб оперативной памяти; видеокарта SVGA, 1280x1024 High Color (32 bit); 2 Мб свободного дискового пространства; операц. система Windows ХР/7/8; Adobe Reader. – Загл. с экрана. – Номер гос. регистрации в ФГУП НТЦ «Информрегистр» __________ свид. № _____ от __.__.____.
ISBN 978-5-8353-1686-1
Учебно-методическое пособие разработано по дисциплине «Дискретная математика» для направления бакалавриата 01.03.02 «Прикладная математика и информатика» в соответствии с требованиями ФГОС ВО и включает краткий теоретический материал, примеры решения задач, методические рекомендации. Может быть использовано для выполнения контрольных работ по дисциплине «Дискретная математика» студентами направлений 02.03.02 «Фундаментальная информатика и информационные технологии» и 02.03.03 «Математическое обеспечение и администрирование информационных систем» и по дисциплине «Дискретная математика и математическая логика» студентами направления 02.03.01 «Математика и компьютерные науки». Предназначено для студентов 1-2 курсов заочной формы обучения института фундаментальных наук.
| Утверждено на заседании кафедры прикладной математики Протокол № 7 от «26» февраля 2018 г. Заведующий кафедрой, ____________________ Е. С. Каган | Рекомендовано научно-методическим советом института фундаментальных наук Рекомендовано Протокол № 7 от «19» марта 2018 г. Председатель совета доцент _____________С. М. Сирик |
© С. Г. Гутова, 2018
© Кемеровский государственный
университет, 2018
Текстовое электронное издание
Минимальные системные требования:
Компьютер: Pentium 3 и выше, 500 МГц; ОЗУ 512 Мб; 2 Мб на жестком диске; видеокарта SVGA, 1280x1024 High Color (32 bit); привод
CD-ROM
Операционная система: Windows ХР/7/8
Программное обеспечение: Adobe Reader
Номер государственной регистрации электронного издания __________.
© С. Г. Гутова, 2018
© Кемеровский государственный
университет, 2018
Оглавление
Введение. 5
ГЛАВА 1. ТЕОРИЯ МНОЖЕСТВ. 6
Тема 1. Множества. 6
Тема 2. Векторы и прямые произведения множеств. Проекция вектора на ось 13
Тема 3. Комбинаторика. 18
Тема 4. Соответствия. 30
Тема 5. Отношения. 37
ГЛАВА 2. ТЕОРИЯ ГРАФОВ.. 45
Тема 6. Способы задания графов. Локальные степени вершин. 45
Тема 7. Маршруты. Расстояние между вершинами графа. Диаметр и центр графа 52
Тема 8. Характеристические числа графов. 57
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ.. 61
1. Индивидуальные задания по теме «Множества». 61
2. Индивидуальные задания по теме «Векторы и прямые произведения множеств. Проекция вектора на ось». 64
3. Индивидуальные задания по теме «Комбинаторика». 66
4. Индивидуальные задания по теме «Соответствия». 69
5. Индивидуальные задания по теме «Отношения». 70
6. Индивидуальные задания по теме «Способы задания графов. Локальные степени вершин». 72
7. Индивидуальные задания по теме «Маршруты. Расстояние между вершинами графа. Диаметр и центр графа». 76
8. Индивидуальные задания по теме «Характеристические числа графов» 80
Литература. 84
Введение
Учебно-методическое пособие разработано по дисциплине «Дискретная математика» для направления 01.03.02 «Прикладная математика и информатика» в соответствии с требованиями ФГОС ВО и включает краткий теоретический материал, примеры решения задач, методические рекомендации.
В результате освоения данной дисциплины формируются компетенции учебного плана по направлению 01.03.02 «Прикладная математика и информатика»:
ОПК-1 – способность использовать базовые знания естественных наук, математики и информатики, основные факты, концепции, принципы теорий, связанных с прикладной математикой и информатикой;
ПК-2 – способность понимать, совершенствовать и применять современный математический аппарат.
Учебно-методическое пособие может быть использованы для выполнения контрольных работ по дисциплине «Дискретная математика» студентами направлений 02.03.02 «Фундаментальная информатика и информационные технологии» и 02.03.03 «Математическое обеспечение и администрирование информационных систем» и по дисциплине «Дискретная математика и математическая логика» студентами направления 02.03.01 «Математика и компьютерные науки». Предназначено для студентов 1-2 курсов заочной формы обучения Института фундаментальных наук.
Учебно-методическое пособие может быть полезны для подготовки к практическим занятиям студентами очной формы обучения по указанным направлениям бакалавриата.
ГЛАВА 1. ТЕОРИЯ МНОЖЕСТВ.
Тема 1. Множества
Множество – один из ключевых объектов математики, в частности, теории множеств. «Множество есть многое, мыслимое нами как единое», говорил Георг Кантор (1845-1918). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением.
Множество можно представить как совокупность некоторых объектов, объединенных по какому-либо признаку.
Множество состоит из элементов. В зависимости от их числа множества различают как конечные или бесконечные. Конечные множества могут состоять из одного или нескольких элементов.
Мощность множества – количество его элементов. Мощность множества М обозначается так: 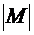 .
.
Множество, не содержащее элементов, называется пустым множеством и обозначается Æ.
Множество обозначают заглавными буквами, а его элементы – прописными. Для записи множества используют фигурные скобки. Например, множество натуральных чисел от 3 до 10: М = {3, 4, 5, 6, 7, 8, 9, 10}.
Говоря об определенном множестве, мы полагаем, что для каждого объекта имеется две возможности: либо он входит в рассматриваемое множество, то есть является его элементом, принадлежит ему (обозначается  ); либо нет (обозначается
); либо нет (обозначается 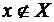 ).
).
Способы задания множества:
- перечисление всех элементов множества, например, множество однозначных неотрицательных чисел X = {0, 1, 2, 3, …, 9};
- указание общего свойства, которым обладают все элементы множества, например, множество четных натуральных чисел X = {2, 4, 6, 8, 10, 12, …} или X = { x: x = 2 n,  };
};
- рекуррентно, например:  ,
,  и др.
и др.
Множество А называют подмножеством множества В (обозначается  ), если каждый элемент множества А является также элементом множества В.
), если каждый элемент множества А является также элементом множества В.
Множества А и В называют равными ( ), если каждый элемент множества А является одновременно элементом множества В и наоборот, то есть если
), если каждый элемент множества А является одновременно элементом множества В и наоборот, то есть если  и
и 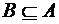 . Другими словами, два множества равны, если они состоят из одних и тех же элементов. Если
. Другими словами, два множества равны, если они состоят из одних и тех же элементов. Если  , но при этом
, но при этом  , то А называется строгим (или собственным) подмножеством В.
, то А называется строгим (или собственным) подмножеством В.
На рисунке 1.1 приведена диаграмма Эйлера-Вьенна [1], где видно, что множество А целиком содержится в множестве В.
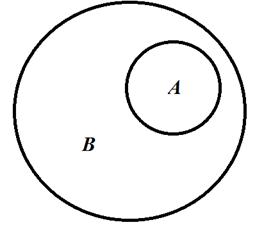
Рис. 1.1. Множество А – строгое подмножество В
Заметим, что контуры на данном рисунке могут иметь любую форму. Чаще всего используются окружности. Поэтому диаграмму Эйлера-Вьенна иначе называют – круги Эйлера.
Множество U называется универсальным множеством (множество всех подмножеств)для некоторой системы множеств, если каждое множество этой системы является подмножеством U, то есть { A, B, C, …}: 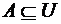 ,
,  ,
,  , …
, …
Дополнениеммножества А называется множество  , состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
На рисунке 1.2 приведена диаграмма, где темным цветом выделено множество  .
.
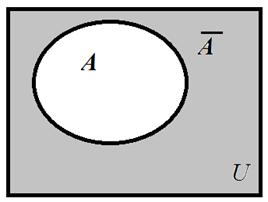
Рис.1.2. Дополнение множества А
Пересечением двух множеств А и В называется множество  , состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
На рисунке 1.3 приведены круги Эйлера, где темным цветом выделено пересечение множеств А и В.

Рис. 1.3. Пересечение множеств А и В
Объединением двух множеств А и В называется множество  , состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно, то есть хотя бы одному из них.
, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно, то есть хотя бы одному из них.
На рисунке 1.4 приведены круги Эйлера, где темным цветом выделено объединение множеств А и В.

Рис. 1.4. Объединение множеств А и В
Разностью двух множеств А и В называется множество  (или
(или  ), состоящее из тех элементов множества А, которые не принадлежат множеству В:
), состоящее из тех элементов множества А, которые не принадлежат множеству В:
 .
.
На рисунке 1.5 приведены круги Эйлера, где темным цветом выделена разность множеств А и В.

Рис. 1.5. Разность множеств А и В
Пример 1.1. Заданы два множества: А = {-2, -1, 0, 1, 2} и B = {0, 2, 4, 5}. Определить множества  ;
;  ;
;  ;
;  и их мощность.
и их мощность.
Решение.
Множество А = {-2, -1, 0, 1, 2} состоит из пяти элементов, следовательно мощность этого множества равна 5:  .
.
Аналогично, B = {0, 2, 4, 5} содержит 4 элемента:  .
.
По определению пересечение двух множеств состоит только из общих для обоих множеств элементов, следовательно,  {0, 2} и
{0, 2} и  .
.
По определению объединение двух множеств состоит из всех элементов, которые принадлежат только множеству А, или только множеству В, или множествам А и В одновременно, следовательно,  = {-2, -1, 0, 1, 2, 4, 5} и
= {-2, -1, 0, 1, 2, 4, 5} и 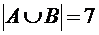 .
.
Множество  является разностью двух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно
является разностью двух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно  {-2, -1, 1} и
{-2, -1, 1} и  .
.
Аналогично, 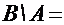 {4, 5} и
{4, 5} и  .
.
Пример 1.2.
Дано универсальное множество U =  ; множества А =
; множества А =  ; В =
; В = 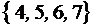 ; С =
; С =  . Найти:
. Найти:  . Записать ответ в виде списка.
. Записать ответ в виде списка.
Решение.
Решаем по действиям.
1) Найдем  . Это множество элементов, которые принадлежат либо А, либо В, либо А и В одновременно. Это означает, что надо составить общий список элементов этих множеств. Так как порядок элементов в множестве произвольный, то при получения объединения А и В сначала выпишем все элементы множества А, затем добавим те элементы множества В, которые еще не встречались. Удобно переобозначить это множество одной буквой, например D.
. Это множество элементов, которые принадлежат либо А, либо В, либо А и В одновременно. Это означает, что надо составить общий список элементов этих множеств. Так как порядок элементов в множестве произвольный, то при получения объединения А и В сначала выпишем все элементы множества А, затем добавим те элементы множества В, которые еще не встречались. Удобно переобозначить это множество одной буквой, например D.
 .
.
2) Найдем множество  . Для этого выпишем те элементы множества U, которые не принадлежат С. Так 1 принадлежит С, значит, ее не включаем в
. Для этого выпишем те элементы множества U, которые не принадлежат С. Так 1 принадлежит С, значит, ее не включаем в  , 2 – принадлежит С, значит, ее не включаем в
, 2 – принадлежит С, значит, ее не включаем в  , 3 – не принадлежит С, значит, ее включаем в
, 3 – не принадлежит С, значит, ее включаем в  , и так далее.
, и так далее.
 .
.
3) Найдем  . Это множество элементов принадлежащих одновременно D и
. Это множество элементов принадлежащих одновременно D и  . Для этого будем брать по очереди элементы D и проверять их наличие в множестве
. Для этого будем брать по очереди элементы D и проверять их наличие в множестве  . Если элемент есть в обоих множествах, включаем его в
. Если элемент есть в обоих множествах, включаем его в  . Например,
. Например, 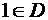 , но
, но 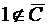 , значит, 1 не включаем в искомое пересечение. Далее,
, значит, 1 не включаем в искомое пересечение. Далее,  , но
, но 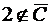 , значит, 2 не включаем в искомое пересечение;
, значит, 2 не включаем в искомое пересечение;  и
и 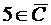 , значит, 5 включаем в искомое пересечение, и так далее.
, значит, 5 включаем в искомое пересечение, и так далее.
 .
.
Пример 1.3.
На диаграмме Вьенна-Эйлера изобразить результат действия
 .
.
Решение.
Решаем по действиям. На каждой копии диаграммы необходимо восстановить контуры всех множеств, участвующих в задании. Они должны пересекаться в самом общем виде. Самый большой контур – универсальное множество. Оно содержит в себе все множества задачи. На рисунке 1.6 приведена такая диаграмма для данного примера. Это основа диаграммы для выполнения каждого действия.
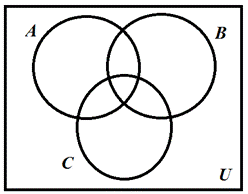
Рис.1.6. Основа диаграммы для трех множеств
1) Изобразим на 1 диаграмме множества, вступающие в 1 действие (действие в скобках). Каждое множество заштриховываем штриховкой своего вида (с наклоном влево, с наклоном вправо, горизонтальной или вертикальной). Множества штрихуются целиком, независимо от их пересечения с другими множествами диаграммы.
На рисунке 1.7 видно, что в результате получилось четыре вида штриховки: левая, правая, двойная и пустая (нет штриховки).
Так как первое действие – разность  , из всех видов штриховки надо выбрать ту одинарную штриховку, которая соответствует множеству А. То есть отбросить ту часть множества А, которая покрыта двойной штриховкой, так как она одновременно является частью множества В. Эту часть мы переносим на 2 копию диаграммы в качестве результата 1 действия.
, из всех видов штриховки надо выбрать ту одинарную штриховку, которая соответствует множеству А. То есть отбросить ту часть множества А, которая покрыта двойной штриховкой, так как она одновременно является частью множества В. Эту часть мы переносим на 2 копию диаграммы в качестве результата 1 действия.

Рис.1.7. Множества, вступающие в 1 действие
2) На 2 копии диаграммы (см. рис. 1.8) надо заштриховать множества, вступающие во второе действие, то есть  и С.
и С.

Рис.1.8. Множества, вступающие во 2 действие
Так как второе действие – пересечение  , то из всех видов штриховки надо выбрать двойную штриховку, которая соответствует общей части множеств D и C. Эту часть мы переносим на 3 копию диаграммы в качестве результата 2 действия, то есть ответа (см. рис. 1.9).
, то из всех видов штриховки надо выбрать двойную штриховку, которая соответствует общей части множеств D и C. Эту часть мы переносим на 3 копию диаграммы в качестве результата 2 действия, то есть ответа (см. рис. 1.9).

Рис.1.9. Ответ
Заметим, что на каждой копии диаграммы, кроме последней, должно быть ровно два вида штриховки, а на последней копии – один вид.
Тема 2. Векторы и прямые произведения множеств. Проекция вектора на ось
Вектор (кортеж) – это упорядоченный набор элементов. Его элементы зазываются координатами или компонентами вектора [2].
Длина (размерность) вектора – число координат вектора.
В отличие от элементов множества, его координаты могут совпадать. Обозначение вектора – в круглых скобках, координаты – через запятую (0, 5, 4, 5, 0, 1). Иногда скобки и даже запятые опускаются. Тогда вектор называют словом: 054501.
Векторы длины 2 называют упорядоченными парами; длины 3 – тройками; и так далее, длины n – n -ками.
Два вектора равны, если они имеют одинаковую длину, и соответствующие координаты равны, то есть:
 ,
,
если  и
и  ,
,  , …,
, …, 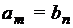 .
.
Прямым (декартовым) произведением двух множеств А и В называется множество  , состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
Прямое произведение n множеств  (обозначается
(обозначается  ) называется множеством всех векторов
) называется множеством всех векторов  , длины n таких, что
, длины n таких, что  ,
,  ,...,
,...,  .
.
Замечание:
 .
.
Теорема (о мощности прямого произведения множеств)
Пусть  - конечные множества и
- конечные множества и  ,
,  ,...,
,...,  . Тогда мощность множества
. Тогда мощность множества  равна произведению мощностей множеств
равна произведению мощностей множеств  :
:
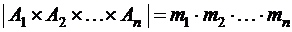 .
.
Следствие: 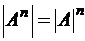 .
.
Пример 2.1. Заданы три множества: А = {0, 1, 2}, B = {4, 6, 8, 10} и С = {g}. Определить множества  ,
, 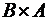 ,
, 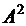 ,
,  ,
, 
Решение.
При получении множества  надо перечислить все пары, составленные их элементов этих множеств. Применяем лексико-графическое упорядочение. По теореме о мощности прямого произведения множеств можно сказать, что искомых пар будет
надо перечислить все пары, составленные их элементов этих множеств. Применяем лексико-графическое упорядочение. По теореме о мощности прямого произведения множеств можно сказать, что искомых пар будет 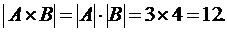
При составлении первой пары в качестве первой координаты берем 1-ый элемент множества А, в качестве второй координаты – 1-ый элемент множества В. Получаем пару (0, 4).
При составлении следующей пары в качестве первой координаты оставляем 1-ый элемент множества А, в качестве второй координаты – 2-ой элемент множества В. Получаем пару (0, 6).
Затем, получаем пары (0, 8), (0, 10). Заметим, здесь первая координата фиксирована, а вторая пробегает весь список возможных элементов множества В.
После этого заменяем первую координату на 1, а вторая координата снова пробегает весь список возможных элементов множества В.
Получаем пары (1, 4), (1, 6), (1, 8), (1, 10). И так далее.
Таким образом, искомое прямое произведение примет вид:
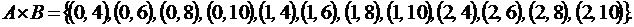 Для получения
Для получения 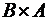 можно поменять метами первые и вторые координаты в каждой паре предыдущего множества. Из чего, в частности, следует, что
можно поменять метами первые и вторые координаты в каждой паре предыдущего множества. Из чего, в частности, следует, что  Но лучше использовать лексико-графический порядок. Элементов этого множества тоже 12. Тогда получим:
Но лучше использовать лексико-графический порядок. Элементов этого множества тоже 12. Тогда получим:
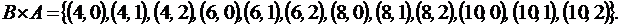 Множество
Множество  строится из тех соображений, что в качестве первой координаты берут элементы «первого» множества А, а в качестве второй – элементы «второго» множества А. Понятно, что в этом случае, часть пар будет заведомо с одинаковыми координатами. Заметим, что
строится из тех соображений, что в качестве первой координаты берут элементы «первого» множества А, а в качестве второй – элементы «второго» множества А. Понятно, что в этом случае, часть пар будет заведомо с одинаковыми координатами. Заметим, что 
 .
.
При построении множества  надо помнить, что его элементами являются уже не пары, а тройки (векторы длины 3). Значит, для перечисления элементов
надо помнить, что его элементами являются уже не пары, а тройки (векторы длины 3). Значит, для перечисления элементов  необходимо сначала зафиксировать 1 элемент А на первом месте и 1 элемент В на втором месте, а третья координата пробегает весь список элементов третьего множества, то есть А. Получаем тройки (0, 4, 0), (0, 4, 1), (0, 4, 2).
необходимо сначала зафиксировать 1 элемент А на первом месте и 1 элемент В на втором месте, а третья координата пробегает весь список элементов третьего множества, то есть А. Получаем тройки (0, 4, 0), (0, 4, 1), (0, 4, 2).
Затем первая координата остается той же, вторая меняется на следующий по списку (второй элемент В), а третья снова пробегает весь список элементов множества А. Получаем тройки (0, 6, 0), (0, 6, 1), (0, 6, 2).
Затем первая координата остается той же, вторая меняется на следующий по списку (третий элемент В), а последняя снова пробегает весь список элементов множества А. Получаем тройки (0, 8, 0), (0, 8, 1), (0, 8, 2).
Последняя группа троек с первой координатой, равной 0 – (0, 10, 0), (0, 10, 1), (0, 10, 2).
Затем надо заменить первую координату на 1 и повторить перебор претендентов на второе и третье место. Затем первую координату полагаем равной 2.
Удобно заранее определить, что количество искомых троек будет найдено по теореме о мощности прямого произведения множеств: 
Тогда 

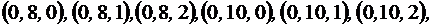


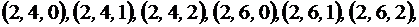
 .
.
Мощность множества  равна
равна 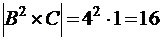 . А именно, четыре с первой координатой 4, четыре с первой координатой 6, четыре с первой координатой 8 и четыре с первой координатой 10.
. А именно, четыре с первой координатой 4, четыре с первой координатой 6, четыре с первой координатой 8 и четыре с первой координатой 10.



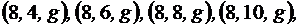
 .
.






