Процесс расширения рабочего тела в диаграмме “ S - I ”
Турбинная ступень состоит из двух лопаточных решеток - сопловой и рабочей, в межлопаточных каналах которых происходит расширение газа. В общем случае газ расширяется последовательно в обеих решетках (реактивный процесс), в частном случае - только в сопловой (активный процесс).
Рассмотренная в предыдущих разделах теория истечения газа из сопел применима к неподвижным (сопловым) и подвижным (рабочим) турбинным решеткам.
Сопловые решетки могут образовывать суживающиеся каналы (для дозвуковых или околозвуковых скоростей) или расширяющиеся сопла Лаваля (для сверхзвуковых скоростей). В обоих случаях проходным сечением, определяющим расход газа, надо считать сечение, имеющее минимальную площадь.
Рабочие решетки, как правило, выполняют конфузорными или с постоянным поперечным сечением по длине канала. Газ входит в эти решетки с относительной скоростью W1, а выходит со скоростью W 2.
На рис.2.2. схематически изображен в координатах S-I процесс расширения газа в реактивной ступени. В турбинной ступени газ расширяется от давления P о* до P 2 по условной политропе AoA2. Располагаемая работа изоэнтропийного расширения газа в ступени определяется по формуле
. (6.1)
Адиабатная работа расширения в сопловой решетке зависит от степени реактивности ступени ρ
L01 = (1-ρ)Lo.
Состояние газа при входе в рабочую решетку определяется точкой A1. Адиабатная работа расширения газа в рабочей решетке составит
. (6.2)
Из уравнения энергии в относительном движении газа через рабочую решетку осевой турбины, для случая энергоизолированного от внешней среды течения без потерь
. (6.3)
Рис. 2.2. Процесс расширения газа в реактивной ступени в диаграмме - si
Выражая состояние газа перед рабочей решеткой в параметрах торможения, найдем на диаграмме -si точку 
(рис.2.2) характеризующую это состояние и адиабатный перепад 
Поскольку 
то вместо равенства (6.3) можно записать
.
Для активного процесса в решетке L02 = 0 и w 2t = w l. Действительная скорость w 2 выхода газа из рабочей решетки меньше w 2t вследствие потерь. Как и для сопловой решетки w 2 можно определить через коэффициент скорости рабочих лопаток φ.
. (6.4)
По аналогии с формулой (5.3)
. (6.5)
Потери энергии на рабочих лопатках
. (6.6)
Для активного процесса в решетке
(6.7)
Состояние газа за решеткой рабочих лопаток можно определить по диаграмме -si или определить аналитически, подобно тому, как это делалось для сопел. Температура газа
(6.8)
Плотность и удельный объем можно определить по формулам
. (6.9)
Если ступень активная и расширение газа на рабочих лопатках не происходит, то Р2 = P1.
Как и в сопловой решетке, процесс истечения газа в решетке рабочих лопаток можно рассчитать по законам политропного расширения.
Аналогично формулам (5.9) и (5.10) для этого случая можно найти показатель условной политропы
, 
. (6.10)
В общем случае величина теплового перепада в сопловых и рабочих решетках переменна по их высоте. Поэтому приведенные выше соотношения надо рассматривать как средние по высоте лопаток или относить их к определенному сечению по высоте лопатки.
Анализ уравнения сохранения энергии.
Рис.2.3. Параметры газа в контрольных сечениях струйки.
Рассмотрим объем газа между сечениями 0-0 и 1-1 в момент времени τ=0(рис.2.3). Условимся записывать работу и теплоту со знаком плюс в случае их подвода к газу и со знаком минус в случае отвода. Теплота трения всегда подводится к газу. По истечении бесконечно малого отрезка времени газ займет новое положение 
. При этом, в общем случае, будет подведено или отведено количество теплоты dQ, внешние и внутренние силы совершат работу dL, изменятся внутренняя энергия U и внешняя энергия Е. В связи с небольшой длиной межлопаточных каналов турбомашин пренебрегаем изменением потенциальной энергии газа, тогда изменение внешней энергий будет равно изменению кинетической энергии рабочего тела.
По закону сохранения энергии сумма изменений внутренней и внешней энергий газа за время dτ должна быть равна сумме подведенного иди отведенного количества теплоты и совершенной работы:
(dU + dE) d τ = dQ d τ + dL d τ, (2.9)
или для 1 кг рабочего тела:
(du + de) d τ = dq d τ + dl d τ. (2.10)
Общие количество теплоты, входящее в эти уравнения складывается из внешнего тепла q внеш, которое может быть со знаком плюс или минус, и внутреннего, эквивалентного работе сил трения
.
Работа внешних и внутренних сил состоит из внешней работы отданной рабочим телом или подведенной к рабочему телу, работы сил трения и работы гидродинамических сил в сечениях 0-0 и 1-1 (работы перемещения)
Следовательно, сумма работ всех сил составит
(2.11)
Подставив (2.11) в (2.10) и предполагая, что процесс течения идет без трения 
тр= 0, и учитывая, что изменение кинетической энергии рабочего тела равно 
, получил после сокращение на dτ
(2.12)
Выражение (2.12) получено для турбины, когда работа отводится от газа и 
имеет знак минус. Оно справедливо для течения без трения и с трением, хотя формально работа трения в выражении не входит. Последнее объясняется тем, что при наличии трения энергия газа уменьшается на величину dlтр и одновременно увеличивается на величину 
, эквивалентную работе сил трения, так как работа трения переходит в теплоту и практически полностью идет на подогрев рабочего тела.
Учитывая, что du + d(p v) = di и проинтегрировав в пределах от сечения 0-0 до сечения 1-1, получим
(2.13)
Уравнение (2.12) и (2.13) можно применять для любого неподвижного канала (сопла, диффузора), для вращающейся решетки или колеса, для ступени турбомашин и для турбомашины в целом. При этом, параметры состояния и скорости газа во входном и выходном сечениях решетки, ступени или машины должны быть постоянными, или надлежащим образом осреднены.
В большинстве случаев процессы в турбомашинзх можно рассматривать как протекающие без теплообмена с окружающей средой, то есть адиабатные; при этом d q внеш =0
Для неподвижного канала (dl внеш = 0, ибо нет перемещения стенок канала. Тогда для изоэнтропийного (без трения) и адиабатного (с трением) процессов течения в неподвижных каналах из уравнения (2.13) получим, соответственно:
(2.14)
Каждое из двух этих уравнений описывает три принципиально отличных процесса течения рабочего тела в неподвижном канале:
1. Процесс идет с ускорением (разгоном) потока С1t> Со, i1t<io (для действительного процесса С1> Со, i1< i0). Газ расширяется в канале, его потенциальная энергия уменьшается, кинетическая - растет. Уравнение (2.14) показывает, что прирост кинетической энергии определяется уменьшением энтальпии рабочего тела.
2. Процесс идет с замедлением (торможением) рабочего тела С1t<Сo, i1 t > i0 (в действительном процессе C1< C 0, i1>io). Потенциальная энергия газа растет за счет его кинетической энергии, которая соответственно уменьшается. Такой процесс осуществляется в диффузоре.
3. Процесс дросселирования i1t = io. При этом имеет место потеря работоспособности рабочего тела.
Располагаемая работа расширения
hc – располагаемая работа расширения в СА.Показатель адиабаты k = 1,4 – для воздухаk = 1,26 – 1,33 – для пара, или степенипонижения давления в СА
Рис. 2.4. располагаемая работа сжатия
Определение параметров течения в изоэнтропийном и реальном процессах расширения.
Широкое распространение при расчетах получили также различные диаграммы водяного пара, в особенности h,s- диаграмма. Вместе с тем следует помнить, что точность расчетов с помощью h,s -диаграммы зависит от масштаба, в котором она построена, и от пределов изменения состояния(рис 2.5).
В настоящее время взаимозависимости термодинамических свойств водяного пара представлены формулами, обеспечивающими точность согласно таблицам водяного пара или аппроксимирующие зависимости, которые обычно запрограммированы в виде различных приложений
Если предположить, что расширение пара происходит без потерь и без теплообмена с внешней средой, то этот процесс называется изоэнтропийным и изменение состояния пара подчиняется уравнению изоэнтропы
Рис. 2.5. Процесс расширения пара в канале, изображенный в h, s -диаграмме
Истечение газа при изоэнтропийном процессе его расширения подробно рассматривается в курсе термодинамики, поэтому здесь приведены лишь основные выводы.
Из уравнения энергии применительно к энергоизолированномурасширению в турбинной решетке от давления Ро* до Р1 без потерь
, (4.1)
где индекс t - указывает на то, что соответствующе параметры являются теоретическими, относящимися к расширению газа без потерь;
Lo1 - работа адиабатного расширения газа в решетке;
iо* - энтальпия, определенная по параметрам торможения (
), то есть с учетом скорости на входе в сопло.
Параметры адиабатно заторможенного потока связаны со статическими параметрами известными формулами
, 
.
Учитывая выражение (2.34) и (2.37) получим
, (4.2)
, (4.3)
где 
- число Маха;
- приведенная скорость потока.
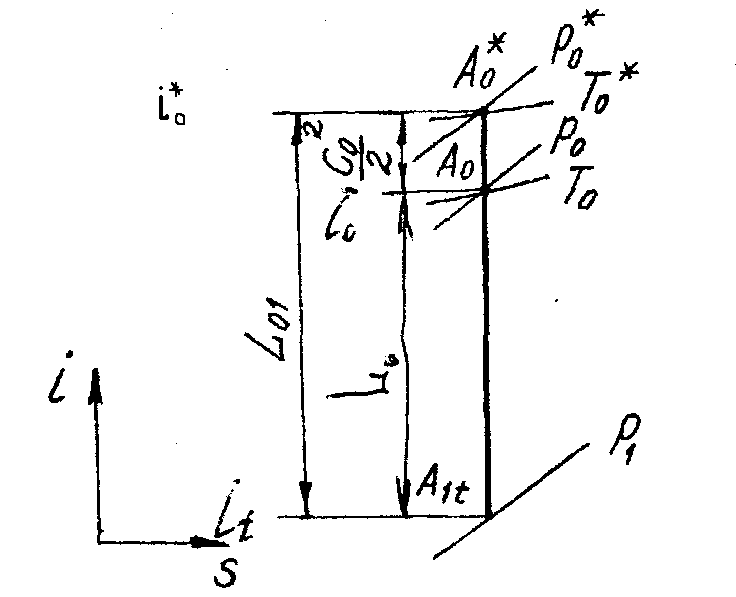
Рис. 2.6. Изоэнтропийный процесс расширения газа в соплах.
Вследствие наличия вязкости действительный процесс истечения газа через сопло сопровождается трением частиц друг о друга, о стенки канала и вихреобразованием, что снижает скорость газа и уменьшает его кинетическую энергию. Вместе с тем, в энергоизолированном процессе по закону сохранения энергии потерянная кинетическая энергия превращается в тепло, вследствие чего температура и энтальпия протекающего газа повышаются.
Действительный процесс расширения газа в сопле происходит по некоторой условной политропе Aо*A1 (рис. 2.7), причем в конечной точке процесса i1> i1t. Действительная скорость на выходе из сопла С1, очевидно, станет меньше теоретической С1t. В действительном процессе скорость истечения определяется по выражению
.
Потеря кинетической энергии в сопле составит
или 
. (5.1)
Рис. 2.7. Процесс расширения газа в сопловом аппарате
Следует заметить, что потеря кинетической энергии 
оказывается меньше работы трения в соплах. Объясняется это тем, что часть работы трения в процессе расширения после превращения в тепловую энергию вновь превращается в кинетическую энергию. Эта часть работы трения называется возвращенным теплом
Коэффициенты потерь, скорости, расхода.
При расчете реального процесса в отличие от изоэнтропийного требует учета сил сопротивления, или коэффициентов трения, или коэффициентов потерь. Расчет каналов и характеристик потока без учета потерь может привести к результатам, существенно отличающимся от действительных. Это в свою очередь снизит эффективность турбины.
При обтекании паром стенки канала, и в частности при обтекании турбинной лопатки, влияние вязкости и вызванных ею сил трения обычно ограничивается небольшой зоной непосредственно около стенки. Скорость потока в этой зоне должна меняться от на стенке, где поток как бы "прилипает" к стенке и полностью заторможен, до скорости в так называемом ядре потока, где влияние сил трения практически уже не сказывается.
Узкая, прилегающая к стенке часть потока, где в данном сечении скорость течения возрастает от нуля до своего полного значения во внешнем потоке, называется пограничным слоем.
В связи с плавным характером перехода пограничного слоя в ядро потока приня-то условно считать, что пограничный слой заканчивается при толщине δ, где скорость отличается от скорости внешнего потока на 1% (рис. 2.8).
Рис. 2.8. Схема пограничного слоя при обтекании плоской стенки:
I - ламинарный режим; II - переходная зона; III - турбулентный режим; IV- ламинарный подслой; 1 - эпюра скоростей идеального потока; 2 - то же в ламинарном слое; 3 - то же в турбулентном слое; 4 - обтекаемая стенка
К.п.д. сопловой решетки
Шаг профилей в решетке оказывает существенное влияние на ее характеристики. С уменьшением шага возрастают профильные потери в связи с увеличением поверхности трения, омываемой единицей количества газа.
С увеличением шага давление на вогнутой поверхности профиля возрастает, на спинке – падает. Это, с одной стороны вызывает увеличение концевых потерь, а с другой - способствует отрыву потока на спинке, где разность давления на выходе из решетки и минимального давления возрастает. Кроме того, снижение давления на спинке при увеличении шага может вызвать появление волновых потерь.
Очевидно, для каждого типа решетки должен существовать оптимальный шаг, при котором КПД решетки достигает максимума. Оптимальные значения шага лопаток должны определяться опытным путем для конкретных решеток и условий их обтекания. Для общей ориентировки можно принять: у реактивных решеток 
, у активных 
Поворот потока в решетке оказывает влияние на ее КПД. Поворот увеличивается с уменьшением суммы углов β1+β2 для рабочей решетки и суммы углов α0+α1 для сопловой решетки. При этом возрастает протяженность диффузорного участка на спинке и повышается опасность отрыва потока, также повышаются концевые потери вследствие интенсификации вторичных течений. С увеличением угла поворота потока коэффициенты скорости 
или 
уменьшаются.
Снижение относительной высоты лопаток 
вызывает, как это следует из раздела 9.2 уменьшение КПД решетки и, следовательно, коэффициентов 
, 
. При 
относительная величина концевых потерь незначительна, однако она резко возрастает при малых значениях 
.
Уменьшение ширины лопатки В при заданной высоте является целесообразным, так как при этом увеличивается относительная высота лопатки 
. По опытам проведенным с тремя типами сопловых венцов, оптимальное отношение b/1 = 1.4 
1. Дальнейшее уменьшение b не приводит к увеличению КПД. Аналогичные исследования рабочих решеток показали, что оптимальная ширина рабочих лопаток находится в области 
=3. Следует отметить, что с уменьшением числа Re они могут возрастать.
При выборе ширины рабочих лопаток необходимо помнить о том, что уменьшение ширины повлечет за собой увеличение числа лопаток и может вызвать трудность в размещении их на диске. Кроме того, в узких лопатках по прочностным и технологическим соображениям не всегда удается выдержать оптимальные толщины входной и выходной кромок. Лопатки газовых турбин чаще всего выполняются с шириной В=(0,25+0,4) 
.
Однако, кроме указанных факторов, надо учитывать еще утечку или подсос газа через осевой зазор, которые вызывают дополнительные искривления линий тока в периферийных областях. На основании проведенных экспериментов рекомендуется принимать величину осевого зазора в пределах 
.
Анализ требуемой формы соплового канала при дозвуковых и сверхзвуковых течениях.
На рис. 2.9 построены кривые, показывающие характер изменения расхода G1t, скорости истечения C1t и удельного объема V 1t в выходном сечении сопла в зависимости от отношения давлений 
при неизменных начальных параметрах рабочего тела.
Рис.2.9. Зависимость расхода через сопло, площади выходногосечения сопла, скорости и удельного объема е выходном сечении ототношения давлений
Из рисунка видно, что в области дозвукового истечения 
при уменьшении β1 (в случае уменьшения давления за соплом) расход возрастает. При критическом течении 
расход становится максимальным. В области сверхзвукового истечения 
расход должен уменьшаться и при β1 = 0 расход должен быть равен нулю.
Опыты подтверждают увеличение расхода через сопло при уменьшении β1 в дозвуковой области истечения, но не подтверждают снижение расхода в области сверхзвукового истечения. В действительности, достигнув наибольшего значения при критическом отношений давлений, расход через сопло в дальнейшем при всех значениях 
остается неизменным и равным максимальному.
Из рисунка 2.9 следует, что форма сопла при дозвуковом и звуковом истечении (М < 1.0) должна быть сходящейся (суживающейся), при сверхзвуковом (М > 1.0) сходяще-расходящейся. В сходящейся части сходяще-расходящегося сопла поток расширяется от начального давления до критического, а в расходящейся - от критического до заданного давления P1<Ркр.
Сходяще-расходящееся сопло называется соплом Лаваля, для краткости будем называть его в дальнейшем расходящимся (расширяющимся) соплом.
В расходящихся соплах выходное сечение не определяет расхода, так как последний зависит не от площади выходного сечения и параметров в этом сечении, а от площади и параметров узкого сечения.
Критические параметры
Лопатки более сложного профиля. Критические параметры - в горле канала.
Можно использовать расширительную способность косого среза сопла, получить скорость С1>а1, В судовыхтурбинах расширительная способность не используется.
В до звуковой области удельный объём растёт медленнее, чем скорость потока, поэтому канал должен быть сходящимся, чтобы поток разгонялся. В сверхзвуковой области удельный объём растёт быстрее, чем скорость, поэтому площадь канала должна увеличиваться (рис. 2.10).
Сопло Лаваля
- степень понижения давления.
Рис.2.10. График дозвуковых и сверхзвуковых скоростей в сопле Лаваля
В области дозвуковых течений при увеличении теплоперепада скорость растёт быстрее, чем удельный объем. В области дозвуковых течений площадь канала должна увеличиваться. При увеличении теплоперепада расход в дозвуковой области будет расти, а в сверхзвуковой будет постоянен, так как скорость достигла скорости звука.
, 
, 
,
.
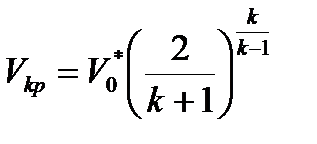