1. Найти область определения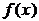 
.
2. Исследовать функцию на четность – нечетность.
3. Найти вертикальные асимптоты и точки разрыва (если есть).
4. Исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты (если есть).
5. Найти экстремумы и интервалы монотонности функции.
6. Найти точки пересечения графика с осями координат и, если это нужно для схематического построения графика, найти дополнительные точки.
7. Схематично построить график.
Подробная схема исследования функции 
и построения графика.
1. Найти область определения .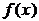
a. Если у 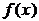есть знаменатель, он не должен обращаться в 0.
b. Подкоренное выражение корня четной степени должно быть неотрицательным (больше либо равно нулю).
c. Подлогарифмическое выражение должно быть положительным.
2. Исследовать функцию на четность – нечетность.
a. Если 
, то функция четная.
b. Если 
, то функция нечетная.
c. Если не выполнено ни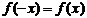 
, ни 
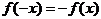, то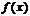 
– функция общего вида.
3. Найти вертикальные асимптоты и точки разрыва (если есть).
a. Вертикальная асимптота может возникнуть только на границе области определения функции.
b. Если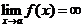 
(
или 
), то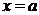 
– вертикальная асимптота графика 
.
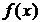4. Исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты (если есть).
a. Если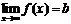 
, то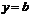 
– горизонтальная асимптота графика .
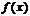b. Если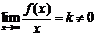 
и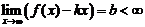 
, то прямая 
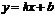является наклонной асимптотой графика 
.
c. Если пределы, указанные в п. a, b, существуют только при одностороннем стремлении 
к бесконечности (
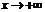или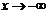 
), то полученные асимптоты будут односторонними: левосторонними при 
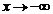и правосторонними при 
.
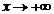5. Найти экстремумы и интервалы монотонности функции.
a. Найти производную 
.
b. Найти критические точки 
(те точки, где 
или где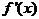 
не существует).
c. На числовой оси отметить область определения 
и ее критические точки.
d. На каждом из полученных числовых интервалов определить знак производной 
.
e. По знакам производной сделать вывод о наличии экстремумов у 
и их типе.
f. Найти экстремальные значения 
.
g. По знакам производной сделать вывод о возрастании и убывании .
6. Найти точки пересечения графика с осями координат и, если это нужно для схематического построения графика, найти дополнительные точки.
a. Для того, чтобы найти точки пересечения графика с осью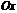 
, надо решить уравнение 
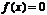. Точки 
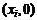, где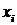 
– нули , будут точками пересечения графика 
с осью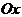 
.
b. Точка пересечения графика 
с осью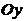 
имеет вид 
. Она существует, только если точка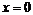 
входит в область определения функции 
.
8. Схематично построить график.
a. Построить систему координат и асимптоты.
b. Отметить экстремальные точки.
c. Отметить точки пересечения графика с осями координат.
d. Схематично построить график так, чтобы он проходил через отмеченные точки и приближался к асимптотам.
Пример. Исследовать функцию 
и схематично построить ее график.
1. 
.
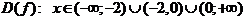2. – функция общего вида.
3. Поскольку 
и 
, то прямые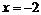 
и 
являются вертикальными асимптотами; точки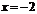 
и 
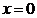являются точками разрыва.
4. Поскольку 
, прямая 
– горизонтальная асимптота графика .
5. 
; 
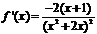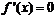при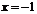 
. На числовой оси отмечаем точки 
, 
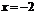(не входят в область определения 
) и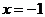 
(критическая точка ). На каждом из полученных числовых интервалов определяем знак производной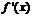 
: при 
, при 
, при 
, при 
. Делаем выводы: 
– точка максимума (в этой точке производная меняет знак с «+» на «–»), 
; при 
и при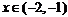 
возрастает; при 
и при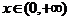 
убывает.
6. Точка пересечения графика с осью :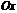 
. Точка пересечения графика с осью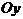 
отсутствует, так как точка 
не входит в область определения функции .
7. См. рис. 7.
16. Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия.
Основные понятия. Частные производные
Определение. Пусть имеется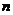 
переменных величин и каждому набору их значений 
из некоторого множества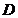 
соответствует одно вполне определенное значение переменной величины 
из множества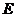 
. тогда говорят, что задана функция нескольких переменных 
.
Переменные 
называются независимыми переменными или аргументами, - зависимая переменная. Множество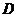 
называется областью определения функции, множество 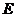- областью значений функции.
Функцию двух переменных будем обозначать как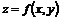 
.
Определение. Графиком функции двух переменных 
называется множество точек трехмерного пространства (
), аппликата 
которых связана с абсциссой 
и ординатой 
функциональным соотношением 
. График представляет собой некоторую поверхность в трехмерном пространстве.
