Пусть в точке 
функция 
непрерывна, а производная 
при переходе через точку меняет знак. Тогда – точка экстремума: максимума, если знак меняется с «+» на «–», и минимума, если с «–» на «+».
Доказательство. Пусть 
при 
и 
при 
.
По теореме Лагранжа 
, где 
.Тогда если 
, то 
; поэтому 
и 
, следовательно, 
, или 
. Если же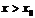 
, то 
; поэтому 
и 
, следовательно, или 
.
Таким образом доказано, что 
в любых точках вблизи , т.е. – точка максимума функции 
.
Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана.
Если при переходе через точку производная не меняет знак, то в точке экстремума нет.
Теорема (второе достаточное условие экстремума). Пусть в точке производная дважды дифференцируемой функции 
равна 0 (
), а ее вторая производная в этой точке отлична от нуля (
) и непрерывна в некоторой окрестности точки . Тогда – точка экстремума 
; при 
это точка минимума, а при 
это точка максимума.
Алгоритм нахождения экстремумов функции с помощью первого достаточного условия экстремума.
1. Найти производную.
2. Найти критические точки функции.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов.
4. Найти экстремальные значения функции.
Алгоритм нахождения экстремумов функции с помощью второго достаточного условия экстремума.
1. Найти производную 
.
2. Найти вторую производную 
.
3. Найти те точки, в которых 
.
4. В этих точках определить знак .
5. Сделать вывод о существовании и характере экстремумов.
6. Найти экстремальные значения функции.
Пример. Рассмотрим 
. Найдем 
. Далее, 
при 
и при 
. Исследуем критические точки с помощью первого достаточного условия экстремума. Имеем, что 
при 
и при 
, и 
при 
. В точках 
и 
производная меняет свой знак: при 
с «+» на «–» и при 
с «–» на «+». Это значит, что в точке 
функция имеет максимум, а точке – минимум; 
. Для сравнения исследуем критические точки с помощью второго достаточного условия экстремума. Найдем вторую производную 
. Имеем: 
, а это значит, что в точке 
функция имеет максимум, а точке 
– минимум.
14. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры.
Определение. Асимптотой графика функции 
называется прямая, обладающая тем свойством, что расстояние от точки 
до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Различают вертикальные (рис. 6.6 а), горизонтальные (рис. 6.6 б) и наклонные (рис. 6.6 в) асимптоты.
На рис. 6.6а изображена вертикальная асимптота.
На рис 6.6б – горизонтальная асимптота.
На рис. 6.6в – наклонная асимптота.
Теорема 1. В точках вертикальных асимптот (например, 
) функция 
терпит разрыв, ее предел слева и справа от точки 
равен 
:
и (или) 
.
Теорема 2. Пусть функция 
определена при достаточно больших 
и существуют конечные пределы
и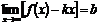 
.
Тогда прямая 
является наклонной асимптотой графика функции 
.
Теорема 3. Пусть функция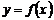 
определена при достаточно больших и существует предел функции 
. Тогда прямая 
есть горизонтальная асимптота графика функции 
.
Горизонтальная асимптота является частным случаем наклонной асимптоты, когда 
. Поэтому, если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример. Найти асимптоты графика функции 
.
Решение. В точке 
функция не определена, найдем пределы функции слева и справа от точки :
; 
.
Следовательно, - вертикальная асимптота.
| Найдем наклонную асимптоту:
 ;
  .
Таким образом,  - наклонная асимптота (рис. 6.7).
|
15. Общая схема исследования функций и построения их графиков. Пример.
