Определение. Функция 
называется возрастающей на интервале 
, если для любых точек 
из этого интервала при выполнении условия 
выполняется неравенство 
(большему значению аргумента соответствует большее значение функции).
Определение. Аналогично, функция 
называется убывающей на интервале 
, если для любых точек 
из этого интервала при выполнении условия 
выполняется неравенство 
(большему значению аргумента соответствует меньшее значение функции).
Возрастающие на интервале 
и убывающие на интервале 
функции называются монотонными на интервале 
.
Знание производной дифференцируемой функции позволяет находить интервалы ее монотонности.
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой на интервале функции 
положительна на интервале , то функция 
монотонно возрастает на этом интервале.
Доказательство. Зафиксируем любые точки на интервале 
такие, что 
.
Тогда по следствию из теоремы Лагранжа 
, где 
. По условию на всем интервале 
, то есть 
, следовательно, 
. Таким образом, 
действительно возрастает на 
, что и требовалось доказать.
Теорема (достаточное условие убывания функции). Если производная дифференцируемой на интервале функции отрицательна на интервале 
, то функция 
монотонно убывает на этом интервале.
Геометрический смысл этих теорем состоит в том, что на интервалах убывания функции касательные к графику функции образуют с осью 
тупые углы, а на интервалах возрастания – острые (см. рис. 4).
Алгоритм нахождения интервалов монотонности функции 
.
- Найти
. - Найти нули производной.
- На числовой оси отметить область определения , нули производной и те точки, где производная не существует.
- На каждом из полученных интервалов определить знак производной
. - Сделать вывод о возрастании или убывании функции
на каждом интервале.
Пример. Пусть 
. Найдем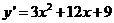 
. Далее, 
при 
и при 
. Имеем, что 
при 
и при 
, и 
при 
. Это значит, что при 
и при 
функция 
возрастает, а при 
функция убывает.
12. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).
Определение. Точка 
называется точкой максимума функции 
, если существует некоторое число 
такое, что для всех 
, удовлетворяющих условию 
, выполнено неравенство 
.
Максимум функции – это значение функции в точке максимума.
На рис 5 показан пример графика функции, имеющей максимумы в точках 
.
Определение. Точка называется точкой минимума функции , если существует некоторое число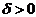 
такое, что для всех 
, удовлетворяющих условию 
, выполнено неравенство 
. На рис 5 функция имеет минимум в точке 
.
Для максимумов и минимумов есть общее название – экстремумы. Соответственно точки максимума и точки минимума называются точками экстремума.
Очевидно, что функция, определенная на отрезке, может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.
В точках экстремума у производной есть особые свойства.
Теорема (необходимое условие экстремума). Пусть в точке 
функция имеет экстремум. Тогда либо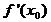 
не существует, либо 
.
Доказательство. Предположим, что функция 
имеет в точке 
максимум.
Тогда при достаточно малых 
при любом знаке верно неравенство: 
, т.е. 
.
Тогда: 
и 
.
По определению производной в точке : 
(если такой предел существует). Т.е. если 
, но 
, то 
, а если 
, но 
, то 
. Возможно это только в тех случаях, если 
или если 
не существует. Теорема доказана.
Те точки из области определения функции, в которых 
не существует или в которых 
, называются критическими точками функции.
Таким образом, из только что доказанной теоремы следует, что точки экстремума лежат среди критических точек. В общем случае критическая точка не обязана быть точкой экстремума. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум.
Пример. Рассмотрим 
. Имеем 
, но точка 
не является точкой экстремума (см. рис 6).
13. Достаточные признаки существования экстремума (доказать одну из теорем).
