Оглавление
1. Предел последовательности и предел функции. Признаки существования предела. 3
2. Определение предела функции в точке. Основные теоремы о пределах. 4
3. Бесконечно малые величины. Бесконечно большие величины.. 5
4. Второй замечательный предел, число е. Понятие о натуральных логарифмах. 6
5. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. 7
6. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке. 8
7. Дифференцируемость функций одной переменной. 9
8. Основные правила дифференцирования функций одной переменной. 10
9. Формулы производных основных элементарных функций. Производная сложной функции. 11
10. Теоремы Ролля и Лагранжа. Геометрическая интерпретация этих теорем. 12
11. Достаточные признаки монотонности функции. 13
12. Определение экстремума функции одной переменной. Необходимый признак экстремума. 14
13. Достаточные признаки существования экстремума. 15
14. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. 16
15. Общая схема исследования функций и построения их графиков. 17
16. Функции нескольких переменных. Частные производные. 18
17. Понятие об эмпирических формулах и методе наименьших квадратов. 19
18. Дифференциал функции и его геометрический смысл. 20
19. Понятие первообразной функции. Неопределенный интеграл и его свойства. 21
20. Метод замены переменной в неопределенном интеграле. 22
21. Метод интегрирования по частям для случаев неопределенного и определенного интегралов. 23
1. Предел последовательности при  и предел функции при
и предел функции при  . Признаки существования предела (с доказательством теоремы о пределе промежуточной функции).
. Признаки существования предела (с доказательством теоремы о пределе промежуточной функции).
Предел числовой последовательности
Определение. Если по некоторому закону каждому натуральному числу  поставлено в соответствие вполне определенное число
поставлено в соответствие вполне определенное число  , то говорят, что задана числовая последовательность
, то говорят, что задана числовая последовательность  :
:
 .
.
Другими словами, числовая последовательность - это функция натурального аргумента: 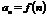 .
.
Числа  называются членами последовательности, а число
называются членами последовательности, а число  - общим или
- общим или  -м членом данной последовательности.
-м членом данной последовательности.
Примеры числовых последовательностей:
1)  (монотонная, неограниченная),
(монотонная, неограниченная),
2)  (не монотонная, ограниченная)
(не монотонная, ограниченная)
3) 
Рассмотрим числовую последовательность  , изобразив ее точками на числовой оси (рис.4.1):
, изобразив ее точками на числовой оси (рис.4.1):

Видно, что члены последовательности  с ростом
с ростом  как угодно близко приближаются к 0. При этом абсолютная величина разности
как угодно близко приближаются к 0. При этом абсолютная величина разности  становится все меньше и меньше.
становится все меньше и меньше.
Определение. Число  называется пределом числовой последовательности
называется пределом числовой последовательности  , если для любого, даже сколь угодно малого положительного числа
, если для любого, даже сколь угодно малого положительного числа  , найдется такой
, найдется такой  (зависящий от
(зависящий от  ), что для всех членов последовательности с номерами
), что для всех членов последовательности с номерами  верно неравенство:
верно неравенство:
 .
.
Обозначают:  . Или
. Или  при
при  .
.
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Предел функции в бесконечности и в точке
Предел функции в бесконечности: С понятием предела числовой последовательности 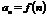 тесно связано понятие предела функции
тесно связано понятие предела функции  в бесконечности. Если в первом случае переменная
в бесконечности. Если в первом случае переменная  возрастая, принимает лишь целые значения, то во втором случае переменная
возрастая, принимает лишь целые значения, то во втором случае переменная  , изменяясь, принимает любые значения.
, изменяясь, принимает любые значения.
Определение. Число  называется пределом функции
называется пределом функции  при
при  стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа
стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа  , найдется такое положительное число
, найдется такое положительное число  (зависящее от
(зависящее от  ), что для всех
), что для всех  таких что
таких что  , верно неравенство:
, верно неравенство:
 .
.
Это предел функции обозначается:  или
или  при
при  .
.
Можно сформулировать понятие предела при стремлении  к бесконечности определенного знака, т.е. при
к бесконечности определенного знака, т.е. при  и при
и при  . В первом случае основное неравенство:
. В первом случае основное неравенство:  должно выполнятся для всех
должно выполнятся для всех  таких, что
таких, что  , а во втором – для всех
, а во втором – для всех  таких, что
таких, что  .
.
Предел функции в точке: Пусть функция  задана в некоторой окрестности точки
задана в некоторой окрестности точки  , кроме, быть может, самой точки
, кроме, быть может, самой точки  .
.
Определение. Число  называется пределом функции
называется пределом функции  при
при  стремящемся к
стремящемся к  (или в точке
(или в точке  ), если для любого, даже сколько угодно малого положительного числа
), если для любого, даже сколько угодно малого положительного числа  , найдется такое положительное число
, найдется такое положительное число  (зависящее от
(зависящее от  ), что для всех
), что для всех  , не равных
, не равных  и удовлетворяющих условию
и удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  .
.
Это предел функции обозначается:  или
или  при
при  .
.
Если при стремлении  к
к  переменная
переменная  принимает лишь значения, меньшие
принимает лишь значения, меньшие  , или наоборот, лишь значения большие
, или наоборот, лишь значения большие  , и при этом функция
, и при этом функция  стремится к некоторому числу
стремится к некоторому числу  , то говорят об односторонних пределах функции
, то говорят об односторонних пределах функции  соответственно слева
соответственно слева  и справа
и справа  .
.
Признаки существования предела
Теорема 1. Если числовая последовательность  монотонна и ограничена, то она имеет предел.
монотонна и ограничена, то она имеет предел.
Теорема 2. Если в некоторой окрестности точки  (или при достаточно больших значениях
(или при достаточно больших значениях  ) функция
) функция  заключена между двумя функциями
заключена между двумя функциями  и
и  , имеющими одинаковый предел
, имеющими одинаковый предел  при
при  (или
(или  ), то функция
), то функция  имеет тот же предел
имеет тот же предел  .
.
Пусть при 
 ,
,  .
.
Это означает, что для любого  найдется такое число
найдется такое число  , что для всех
, что для всех  и удовлетворяющих условию
и удовлетворяющих условию  будут верны одновременно неравенства:
будут верны одновременно неравенства:
 (1.1)
(1.1)
или

Т.к. по условию функция  заключена между двумя функциями, т.е.:
заключена между двумя функциями, т.е.:
 , то из неравенств (1.1) следует, что
, то из неравенств (1.1) следует, что  , т.е.:
, т.е.:
 .
.
А это и означает, что 
2. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать).
Предел функции в точке
Определение. Число  называется пределом функции
называется пределом функции  при
при  стремящемся к
стремящемся к  (или в точке
(или в точке  ), если для любого, даже сколько угодно малого положительного числа
), если для любого, даже сколько угодно малого положительного числа  , найдется такое положительное число
, найдется такое положительное число  (зависящее от
(зависящее от  ), что для всех
), что для всех  , не равных
, не равных  и удовлетворяющих условию
и удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  .
.
Это предел функции обозначается:  или
или  при
при  .
.
Основные теоремы о пределах. Признаки существования предела
Пусть  и
и  - функции, для которых существуют пределы при
- функции, для которых существуют пределы при  (
( ):
):  ,
,  .
.
Сформулируем основные теоремы о пределах:
1) Функция не может иметь более одного предела.
Предположим противное, т.е. что функция  имеет 2 предела А и D,
имеет 2 предела А и D,  . Тогда на основании теоремы о связи бесконечно малых величин с пределами функции:
. Тогда на основании теоремы о связи бесконечно малых величин с пределами функции:  ,
, 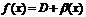 , где
, где  и
и 
 - бесконечно малые величины при
- бесконечно малые величины при  (
( ). Вычитая почленно эти равенства, получим:
). Вычитая почленно эти равенства, получим:  , откуда
, откуда  . Это равенство невозможно, т.к. на основании свойства 1 бесконечно малых
. Это равенство невозможно, т.к. на основании свойства 1 бесконечно малых  это величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно.
это величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно.
2) Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.
 .
.
3) Предел произведения конечного числа функций равен произведению пределов этих функций, т.е.
 .
.
По условию  и
и  , следовательно, на основании теоремы о связи бесконечно малых величин с пределами функции:
, следовательно, на основании теоремы о связи бесконечно малых величин с пределами функции:  ,
,  , где
, где  и
и  - бесконечно малые величины при
- бесконечно малые величины при  (
( ). Перемножая почленно оба равенства, получим:
). Перемножая почленно оба равенства, получим:
 .
.
На основании свойств бесконечно малых последние три слагаемые представляют величину, бесконечно малую  при
при  (
( ).
).
Итак, функция  представляет сумму постоянного числа
представляет сумму постоянного числа  и бесконечного малой
и бесконечного малой  . На основании обратной теоремы о связи бесконечно малых с пределами функции это означает, что
. На основании обратной теоремы о связи бесконечно малых с пределами функции это означает, что  .
.
В частности, постоянный множитель можно выносить за знак предела, т.е.
 .
.
Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е.
 ,
,  .
.
5) Если  ,
,  , то предел сложной функции
, то предел сложной функции
 .
.
6) Если в некоторой окрестности точки  (или при достаточно больших
(или при достаточно больших  )
)  , то
, то
 .
.
3. Бесконечно малые величины (определение). Свойства бесконечно малых (одно из них доказать). Бесконечно большие величины, их связь с бесконечно малыми.
Бесконечно малые величины
Определение. Функция  называется бесконечно малой величиной при
называется бесконечно малой величиной при  или при
или при  , если ее предел равен нулю:
, если ее предел равен нулю:
 .
.
Связь бесконечно малых величин с пределами функций
Теорема 1. Если функция  имеет при
имеет при  (
( ) предел, равный
) предел, равный  , то ее можно представить в виде суммы этого числа
, то ее можно представить в виде суммы этого числа  и бесконечно малой
и бесконечно малой  при
при  (
( ), т.е.
), т.е.
 .
.
Теорема 2. Если функцию  можно представить как сумму числа
можно представить как сумму числа  и бесконечно малой
и бесконечно малой  при
при  (
( ), то число
), то число  есть предел этой функции при
есть предел этой функции при  (
( ), т.е.
), т.е.
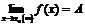 .
.
Свойства бесконечно малых величин
1) Алгебраическая сумма конечного числа бесконечного малых величин есть величина бесконечно малая.
По условию  и
и  - бесконечно малые величины при
- бесконечно малые величины при  . Это означает, что для любого
. Это означает, что для любого  найдутся такие числа
найдутся такие числа  , что для всех
, что для всех  и удовлетворяющих условиям:
и удовлетворяющих условиям:
 и
и  (1.1)
(1.1)
выполняются соответствующие неравенства:
 и
и  . (1.2)
. (1.2)
Если взять в качестве числа  минимальное из чисел
минимальное из чисел  и
и  , т.е.
, т.е.  , то неравенству
, то неравенству  будут удовлетворять решения обоих неравенств (1.1), а, следовательно, одновременно будут верны неравенства (1.2). Складывая почленно неравенства (1.2), получим, что;
будут удовлетворять решения обоих неравенств (1.1), а, следовательно, одновременно будут верны неравенства (1.2). Складывая почленно неравенства (1.2), получим, что;
 .
.
Используя свойство абсолютных величин, т.е.  , придем к более сильному неравенству:
, придем к более сильному неравенству:
 (1.3)
(1.3)
Итак, для любого  существует такое
существует такое  , что для всех
, что для всех  и удовлетворяющих условию
и удовлетворяющих условию  верно неравенство (1.3). А это означает, что функция
верно неравенство (1.3). А это означает, что функция  есть величина бесконечно малая.
есть величина бесконечно малая.
2) Произведение бесконечно малой величины на ограниченную функцию (в т.ч. на постоянную, на другую бесконечно малую) есть величина бесконечно малая.
3) Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Отношение двух бесконечно малых (неопределенность вида  ) в зависимости от характера изменения переменных в числителе и знаменателе может оказаться или числом, или бесконечно малой или бесконечностью.
) в зависимости от характера изменения переменных в числителе и знаменателе может оказаться или числом, или бесконечно малой или бесконечностью.
Бесконечно большие величины
Определение. Функция  называется бесконечно большой при
называется бесконечно большой при  , если ее предел равен бесконечности:
, если ее предел равен бесконечности:
 .
.
Свойства бесконечно больших величин
1) Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
2) Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
3) Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.
Об отношении или разности двух бесконечно больших функций никакого общего заключения сделать нельзя. В этих случаях говорят о неопределенностях вида  или
или  . В зависимости от характера изменения бесконечно больших величин их отношение или разность может оказаться или числом, или бесконечно малой, или бесконечно большой.
. В зависимости от характера изменения бесконечно больших величин их отношение или разность может оказаться или числом, или бесконечно малой, или бесконечно большой.
Связь между бесконечно малыми и бесконечно большими величинами
Теорема. Если функция  есть бесконечно малая величина при
есть бесконечно малая величина при  (
( ), то функция
), то функция  является бесконечно большой при
является бесконечно большой при  (
( ). И, наоборот, если функция
). И, наоборот, если функция  бесконечно большая при
бесконечно большая при  (
( ), то функция
), то функция  есть величина бесконечно малая при
есть величина бесконечно малая при  (
( ).
).
4. Второй замечательный предел, число е. Понятие о натуральных логарифмах.
Второй замечательный предел.
Определение. Числом  (вторым замечательным пределом) называется предел числовой последовательности
(вторым замечательным пределом) называется предел числовой последовательности  :
:
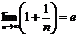 , где
, где 
Прямым вычислением можно убедиться, что  ,
,  (иррациональное число, число Эйлера).
(иррациональное число, число Эйлера).
Если рассмотреть функцию  , то при
, то при  функция имеет предел, равный числу
функция имеет предел, равный числу  :
:
 .
.
Или если  , то
, то  .
.
Непосредственное вычисление этого предела приводит к неопределенности  . Однако доказано, что он равен числу
. Однако доказано, что он равен числу  . Второй замечательный предел необходимо всегда использовать при раскрытии неопределенности вида
. Второй замечательный предел необходимо всегда использовать при раскрытии неопределенности вида  .
.
Число  (число Эйлера, неперово число) играет важную роль в математическом анализе. График функции
(число Эйлера, неперово число) играет важную роль в математическом анализе. График функции 
Рассмотрим примеры вычисления пределов. Получил название экспоненты. Широко используются логарифмы по основанию  , называемые натуральными. Натуральные логарифмы обозначаются символом
, называемые натуральными. Натуральные логарифмы обозначаются символом  .
.
Пример. 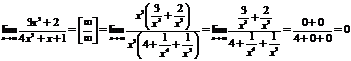 .
.
Пример.  =
=  .
.
Пример.  .
.
Пример. 


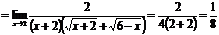 .
.
Пример.  .
.
Пример. 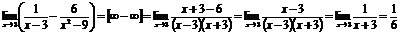 .
.
Пример. 
 .
.
5. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры.
Непрерывность функции
Определение 1. Функция  называется непрерывной в точке
называется непрерывной в точке  , если она удовлетворяет следующим условиям:
, если она удовлетворяет следующим условиям:
1) определена в точке  , т.е. существует
, т.е. существует  ;
;
2) имеет конечные односторонние пределы функции при  слева и справа;
слева и справа;
3) эти пределы равны значению функции в точке  , т.е.
, т.е.
 .
.
Пример. Исследовать функции на непрерывность в точке  :
:
а)  , б)
, б)  .
.
Решение. а)  . При
. При  функция определена,
функция определена,  ,
,  ,
,  , т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция
, т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция  в точке
в точке  непрерывна.
непрерывна.
б)  . При
. При  функция не определена;
функция не определена;  ;
;  .
.
Т.о. в точке  функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.
функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.
Определение 2. Функция  называется непрерывной в точке
называется непрерывной в точке  , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:  .
.
Определения 1 и 2 равносильны.
Точка  называется точкой разрыва функции
называется точкой разрыва функции  , если эта функция в данной точке не является непрерывной. Различают точки разрыва:
, если эта функция в данной точке не является непрерывной. Различают точки разрыва:
Первого рода – когда существуют конечные односторонние пределы функции слева и справа при  , не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при
, не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при  существует, но не равен значению функции в этой точке.
существует, но не равен значению функции в этой точке.
Второго рода – когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.
Свойства функций, непрерывных в точке
1. Если функции  и
и  непрерывны в точке
непрерывны в точке  , то их сумма
, то их сумма  , произведение
, произведение  и частное
и частное  (при условии
(при условии  ) являются функциями, непрерывными в точке
) являются функциями, непрерывными в точке  .
.
2. Если функция  непрерывна в точке
непрерывна в точке  и
и  , то существует такая окрестность точки
, то существует такая окрестность точки  , в которой
, в которой  .
.
Доказательство этого свойства основывается на том, что при малых приращениях аргумента  можно получить как угодно малое приращение функции
можно получить как угодно малое приращение функции  в окрестностях
в окрестностях  не изменится.
не изменится.
3. Если функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция  непрерывна в точке
непрерывна в точке  . Доказательство состоит в том, что малому приращению аргумента
. Доказательство состоит в том, что малому приращению аргумента  соответствует как угодно малое приращение
соответствует как угодно малое приращение  , приводящее в свою очередь к непрерывности функции
, приводящее в свою очередь к непрерывности функции  к как угодномалому приращению
к как угодномалому приращению  .
.
Свойство можно записать:  ,
,
Т.е. под знаком непрерывной функции можно переходить к пределу.
Определение. Функция  называется непрерывнойна промежутке
называется непрерывнойна промежутке  , если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.
, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.
Точки разрыва функции
Определение. Если в какой-нибудь точке  для функции
для функции  не выполняется по крайней мере одно из условий непрерывности, то эта точка называется точкой разрыва функции.
не выполняется по крайней мере одно из условий непрерывности, то эта точка называется точкой разрыва функции.
Причем: 1) Если существуют конечные односторонние пределы функции, неравные друг другу:  , то точка
, то точка  - точка разрыва I рода.
- точка разрыва I рода.
2) Если хотя бы один из односторонних пределов функции  или
или  равен бесконечности или не существует, то точка
равен бесконечности или не существует, то точка  - точка разрыва II рода.
- точка разрыва II рода.
Свойства функций, непрерывных на отрезке
1. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она ограничена на этом отрезке. (рис. 1.1)
, то она ограничена на этом отрезке. (рис. 1.1)
2. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она достигает на этом отрезке наименьшего значения
, то она достигает на этом отрезке наименьшего значения  и наибольшего значения
и наибольшего значения  (теорема Вейерштрасса). (рис. 1.2)
(теорема Вейерштрасса). (рис. 1.2)
 3. Если функция
3. Если функция  непрерывна на отрезке
непрерывна на отрезке  и значения ее на концах отрезка
и значения ее на концах отрезка  и
и  имеют противоположные знаки, то внутри отрезка найдется точка
имеют противоположные знаки, то внутри отрезка найдется точка  такая, что
такая, что  . (Теорема Больцано-Коши.)
. (Теорема Больцано-Коши.)
 Пример. Исследовать на непрерывность и найти точки разрыва функции
Пример. Исследовать на непрерывность и найти точки разрыва функции  . Установить характер разрыва.
. Установить характер разрыва.
Решение. При  функция не определена, следовательно, функция в точке
функция не определена, следовательно, функция в точке  терпит разрыв:
терпит разрыв:  , а
, а  . Так как односторонние пределы бесконечны, то
. Так как односторонние пределы бесконечны, то  - точка разрыва второго рода.
- точка разрыва второго рода.
6. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке.
Определение производной
Пусть на некотором промежутке Х определена функция y = f (x). Возьмем любую точку  . Зададим аргументу х произвольное приращение ∆ х ≠ 0 такое, что точка х +∆ х также будет принадлежать Х. Функция получит приращение ∆ у = f (x +∆ х)− f (x).
. Зададим аргументу х произвольное приращение ∆ х ≠ 0 такое, что точка х +∆ х также будет принадлежать Х. Функция получит приращение ∆ у = f (x +∆ х)− f (x).
Определение. Производной функции y = f (x) в точке х называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует).
Для обозначения производной функции y = f (x) в точке х используются символы у ′(х) или f ′ (x).
Итак, по определению,  .
.
Если для некоторого значения х 0 выполняется условие
 или
или  ,
,
т.е. пределы равны бесконечности, то говорят, что в точке х 0 функция имеет бесконечную производную.
Если функция y = f (x)имеет конечную производную в каждой точке  , то производную f ′ (x) можно рассматривать как функцию х, также определенную на Х. Нахождение производной функции называется дифференцированием функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.
, то производную f ′ (x) можно рассматривать как функцию х, также определенную на Х. Нахождение производной функции называется дифференцированием функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х, называется дифференцируемой на этом промежутке.
Задача о касательной
Пусть на плоскости 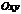 дана непрерывная функция
дана непрерывная функция  и необходимо найти уравнение касательной к этой кривой в точке
и необходимо найти уравнение касательной к этой кривой в точке  .
.

| Уравнение прямой по точке  , принадлежащей этой прямой, и угловому коэффициенту имеет вид: , принадлежащей этой прямой, и угловому коэффициенту имеет вид:
 ,
где ,
где  , ( , ( - угол наклона прямой).
Из - угол наклона прямой).
Из  (рис.5.1) найдем тангенс угла наклона секущей (рис.5.1) найдем тангенс угла наклона секущей  : :  .
Если точку .
Если точку  приближать к точке приближать к точке  , то угол , то угол  будет стремиться к углу будет стремиться к углу  , т.е.
при , т.е.
при   .
Следовательно, .
Следовательно,  . .
|
Из задачи о касательной следует геометрический смысл производной: производная f ′ (x 0) есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой у= f ′ (x) в точке х 0, т.е. k = f ′ (x 0).
Следовательно, уравнение касательной к кривой y = f (x) в точке х 0 примет вид

Пример. Найти производную функции f (x)= х 2.
Решение. Придавая аргументу х приращение ∆ х, найдем соответствующее приращение функции:

Составим отношение:

Найдем предел этого отношения при ∆ х → 0:

7. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему).
Понятие дифференцируемости функции
Определение. Функция y= f (x) называется дифференцируемой в точке х, если ее приращение Δ у в этой точке можно представить в виде
 ,
,
где А – некоторое число, не зависящее от  , а α(
, а α( ) – функция аргумента
) – функция аргумента  , являющаяся бесконечно малой при
, являющаяся бесконечно малой при  →0, т.е.
→0, т.е. 
Выясним теперь связь между дифференцируемостью в точке и существованием производной в той же точке.
Теорема. Для того чтобы функция f (x) была дифференцируемой в данной точке х, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Связь между дифференцируемостью функции и ее непрерывностью
Пример. Доказать, что функция y =│ х │ недифференцируема в точке х =0.
Решение. Производная функции (если она существует) равна

Очевидно, что при х =0 производная не существует, так как отношение  , т.е. не имеет предела при Δ х →0 (ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке х =0.
, т.е. не имеет предела при Δ х →0 (ни конечного, ни бесконечного). Геометрически это означает отсутствие касательной к кривой в точке х =0.
Теорема. Если функция y= f(x) дифференцируема в точке х0,, то она в этой точке непрерывна.
□Доказательство. По условия функция y= f (x) дифференцируема в точке х 0, т.е. существует конечный предел

где f′ (x0) – постоянная величина, не зависящая от  .
.
Тогда на основании теоремы о связи бесконечно малых величин с пределами функций можно записать

где α(∆х) является бесконечно малой величиной при  →0, или
→0, или
 .
.
При Δ х →0 на основании свойств бесконечно малых величин устанавливаем, что Δ у →0 и, следовательно, по определению непрерывности функции в точке, делаем вывод, что функция непрерывна в токе х0. ■
Обратная теорема, вообще говоря, неверна, если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке. Так, функция y =│ х │ непрерывна в точке х0 =0, ибо  но, как было доказано ранее недифференцируема в этой точке.
но, как было доказано ранее недифференцируема в этой точке.
Таким образом, непрерывность функции – необходимое, но не достаточное условие ее дифференцируемости.
Замечание: Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке Х, то функция называется гладкой на этом промежутке. Если же производная функция допускает конечное число точек разрыва, то такая функция на данном промежутке называется кусочно гладкой.
8. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
Производная функции  м.б. найдена по схеме:
м.б. найдена по схеме:
1) Дадим аргументу приращение  и найдем наращение значений функции
и найдем наращение значений функции  .
.
2) Находим приращение функции  .
.
3) Составляем отношение  .
.
4) Находим предел этого отношения при  , т.е.
, т.е.  (если этот предел существует).
(если этот предел существует).
Основные правила дифференцирования
1. Производная постоянной равна нулю, т.е.  .
.
□ Д о к а з а т е л ь с т в о.
При любых  и
и  имеем
имеем  и
и 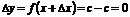 . Отсюда при любом
. Отсюда при любом  отношение
отношение  и, следовательно,
и, следовательно,  ■
■
2. Производная аргумента равна единице, т.е.  .
.
□ Д о к а з а т е л ь с т в о.
Рассмотрим функцию  . При любых
. При любых  и
и  имеем
имеем  и
и 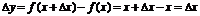 . Отсюда при любом
. Отсюда при любом  отношение
отношение  и, следовательно,
и, следовательно,  ■
■
3. Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.е.
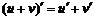 .
.
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.
 .
.
□ Д о к а з а т е л ь с т в о.
Пусть  и
и  - дифференцируемые функции. Найдем производную функции
- дифференцируемые функции. Найдем производную функции  по схеме:
по схеме:
1) Дадим аргументу  приращение
приращение  . Тогда функции
. Тогда функции  и
и 






