Горизонтальные проекции точек определяем с помощью параллелей конуса.
Определяем видимость кривой, учитывая, что проекция линии пересечения видима, если она принадлежит видимой части одной и второй поверхности
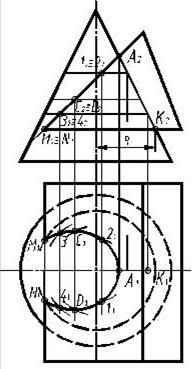
Выполнение задания начинают с построения координационных осей X, Y, Z так, чтобы размеры фронтальной и горизонтальной плоскостей проекций были примерно одинаковы. Затем, по числовым значениям координат, которые берутся из таблицы в соответствии с номером варианта, строятся проекции точек А,В,С, D и соединяются тонкими линиями. Таким способом получают две проекции пирамиды. После этого обозначают проекции точек E, G, K, L.
Рис.79. Пересечение конуса и призмы
На горизонтальной плоскости проекции последовательно соединяют проекции точек k, g, u,е тонкими линиями, в результате чего образуется горизонтальная проекция основания призмы. Фронтальную проекцию приемы получают путём построения перпендикуляров к оси X в точках e 1, k 1, l 1, g 1 высотой h, которые являются проекциями боковых рёбер призмы. Невидимые рёбра проводятся штриховыми линиями. Соединяя концы крайних проекций ребер призмы прямой линией, параллельной оси X, получают фронтальную проекцию верхнего основания призмы. Построение линии пересечения многогранников можно осуществить двумя путями. Либо определить точки пересечения рёбер одного многогранника с гранями другого и рёбер второго с гранями первого, либо построить линии пересечения граней, как плоскостей, одного многогранника с гранями другого. Выбор пути решения делается после анализа условий задачи. Анализ условий данной задачи показывает, что боковые грани параллелепипеда являются профильными плоскостями.
Тема 4-3. Пересечение криволинейных поверхностей с криволинейными поверхностями
Пересечение поверхностей конуса и цилиндра. Построение линии пересечения поверхностей осуществляется при помощи вспомогательных секущих поверхностей. При этом данные поверхности пересекаются вспомогательной поверхностью и определяются линии пересечения каждой из данных поверхностей со вспомогательной. Если эти линии пересекаются (а они, в силу принадлежности одной и той же вспомогательной поверхности, могут пересекаться, касаться или не иметь общих точек), то полученные точки пересечения принадлежат обеим данным поверхностям и, следовательно, их линии пересечения.
Если в качестве вспомогательных секущих поверхностей используются плоскости, то способ построения называют способом вспомогательных плоскостей. Если используются сферы - способом вспомогательных сфер. Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения цилиндра с конусом вращения (рис.80).
Для построения линии пересечения заданных поверхностей удобно в качестве вспомогательных поверхностей использовать серию горизонтальных плоскостей, перпендикулярных оси конуса, которые пересекают цилиндр и конус по окружностям. На пересечении этих окружностей находят точки искомой линии пересечения.
 Известно, что если ось поверхности вращения проходит через центр сферы и сфера пересекает эту поверхность, то линия пересечения сферы и поверхности вращения - окружность, плоскость которой перпендикулярна оси поверхности вращения. При этом, если ось поверхности вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой линии. Это свойство используют для построения линии взаимного пересечения двух поверхностей вращения с помощью вспомогательных сфер. При этом могут быть использованы концентрические и неконцентрические сферы. Рассмотрим применение вспомогательных концентрических сфер - сфер с постоянным центром.
Известно, что если ось поверхности вращения проходит через центр сферы и сфера пересекает эту поверхность, то линия пересечения сферы и поверхности вращения - окружность, плоскость которой перпендикулярна оси поверхности вращения. При этом, если ось поверхности вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой линии. Это свойство используют для построения линии взаимного пересечения двух поверхностей вращения с помощью вспомогательных сфер. При этом могут быть использованы концентрические и неконцентрические сферы. Рассмотрим применение вспомогательных концентрических сфер - сфер с постоянным центром.
Рис. 80. Пример построения линии пересечения конуса и цилиндра с помощью вспомогательных секущих плоскостей
| Пересечение конуса и цилиндра | |
|
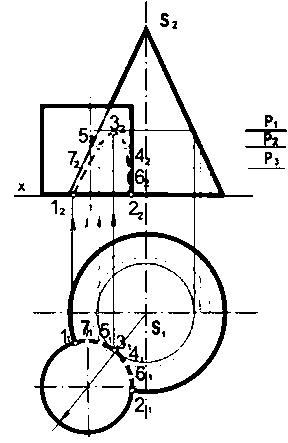
Для построения промежуточных точек 5, 6 и 7, 8 проводят концентрическую шаровую поверхность несколько большего диаметра. Эта сферическая поверхность пересекает конус по окружности несколько меньшего диаметра, а цилиндр — по двум окружностям равных диаметров. Все три окружности проецируются на фронтальную плоскость проекций П 2 в виде прямых, пересечение которых определяет фронтальные проекции 5262 и 7282 промежуточных точек 5,6,7 и 8.
Рис. 81. Пересечение цилиндра и конуса
Так как направление проецирования s перпендикулярно к фронтальной плоскости, то точки 5 и 6,7 и 8 проецируются на нее, попарно сливаясь. Построение горизонтальной проекции линии пересечения не вызывает затруднений, поскольку имеются фронтальные и профильные проекции точек. При отсутствии профильной проекции горизонтальные проекции точек находят также достаточно легко в связи с тем, что точки лежат на окружностях, которые проецируются на горизонтальную плоскость проекций П1 без искажения. Заметим, что фронтальная проекция кривой пересечения может быть построена при отсутствии двух других проекций пересекающихся поверхностей. Другой особенностью способа секущих поверхностей является то, что при его применении требуется повышенная точность построений; окружности, изображающие шаровые поверхности, приходится проводить на очень близком расстоянии друг от друга; это является недостатком способа. Когда оси цилиндра и конуса не пересекаются между собой (рис. 82), то задачу решают с помощью секущих параллельных плоскостей. В приведенном примере проводят горизонтальные плоскости μ, μ', μ", и др., не обозначенные на чертеже. Такие плоскости рассекают конус по окружности, а цилиндр - по прямоугольникам. Как окружности, так и прямоугольники проецируются на горизонтальную плоскость проекций без искажения. Пересечение линий этих фигур между собой позволяет определить точки, принадлежащие линии пересечения поверхностей. При решении в первую очередь определяют опорные точки: 1 в 2 на левой образующей конуса, 3 и 4 на верхней образующей цилиндра, 5 и 6 на правой образующей цилиндра (являются последними видимыми точками кривой при проецировании на плоскость П1, 7 и 8 на нижней образующей цилиндра. Точки 3 и 4 находят, проводя плоскость μ, касательную к цилиндру. Эта плоскость пересекает правую образующую конуса в точке А. Найдя проекции А2 и А1, из центра S1 проводят окружность радиусом S1A1, которая пересечет горизонтальную проекцию верхней образующей цилиндра в точках З 1 и 4 1, Для получения точек 5 и 6 используют окружность радиуса S1B1 и т. д.
Рис. 82. Пересечение шара с различными поверхностями
Промежуточные вспомогательные плоскости целесообразно проводить симметрично по отношению к оси цилиндра; при этом точки 9, 10 и 11, 12 находят на одной вертикальной линии связи. Около точек 5 и 6, где линия пересечения резко меняет кривизну, следует найти дополнительные точки. На рис. 82, а изображен шар, пересекающийся с различными поверхностями вращения: конусом, цилиндром и круговым кольцом. Центр шара при этом лежит на осях поверхностей вращения. Через точки пересечения 12 и 22 контуров конуса и шара проводят горизонтальную плоскость μ. Она пересечет конус по окружности диаметра 7222; шар также пересечется по окружности диаметра 1222; следовательно, эта окружность будет являться линией пересечения шара с конусом. Такое же рассуждение можно применить к цилиндру и любой другой поверхности вращения. Главное удобство при этом состоит в том, что окружность проецируется в виде прямой. Итак, шар, центр которого находится на оси поверхности вращения, пересекается с ней по окружности. Простейшие примеры на пересечение конуса и цилиндра решают способом пересечения их параллельными плоскостями. В более сложных случаях пересечение параллельными плоскостями не дает удовлетворительного решения. Так бывает, в частности, в том случае, когда одна или обе поверхности заданы в наклонном положении. В подобных случаях задачу решают способом секущих шаровых поверхностей. Этот способ применим при следующих условиях: обе пересекающиеся поверхности должны быть поверхностями вращения; оси заданных поверхностей вращения должны пересекаться между собой; точка их пересечения будет являться центром секущих шаровых поверхностей; оси поверхностей вращения должны быть расположены параллельно какой-либо плоскости проекций.
| |
а б
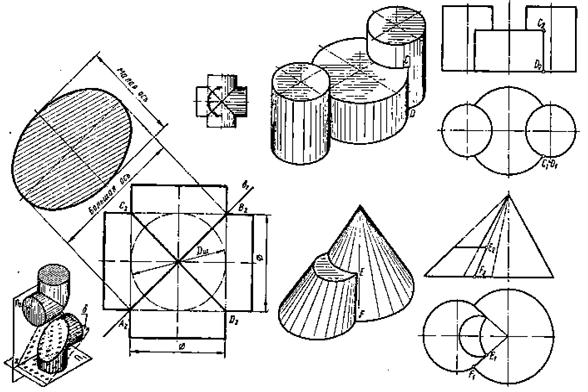
Рис.83. Построение пересечения криволинейных поверхностей: а) двух цилиндров;
б) двух конусов
Отсюда следует: 1) если две цилиндрические или конические, или одна коническая, а другая цилиндрическая поверхности описаны вокруг сферической поверхности (и, следовательно, оси их, пересекаясь, проходят через центр сферы), то они пересекаются по плоским кривым (эллипсам);
2) если же их оси вращения расположены параллельно любой плоскости проекций, то проекция линий пересечения на эту плоскость изобразится отрезками прямых. Приведенные примеры встречаются при изображении взаимно пересекающихся отверстий, труб и др.
Наконец, есть случай, когда пересечение поверхностей вращения выявляется прямой линией, например, когда линии пересечения совпадают с образующими





 При построении линии пересечения цилиндра и конуса, оси которых пересекаются в точке О (рис. 81), прежде всего отмечают фронтальные проекции 12 и 22 крайних левой и правой точек линии пересечения; затем находят фронтальные проекции З1 и 42 нижних точек кривой. Для их определения проводят из центра O2 окружность, являющуюся фронтальной проекцией шара, вписанного в цилиндр. Касание шара к цилиндру произойдет по окружности, фронтальная проекция которой изобразится прямой, проходящей через точку O2. С конусом шар пересечется по окружности, параллельной основанию конуса; фронтальная проекция этой окружности спроецируется в прямую, перпендикулярную к первой прямой; их пересечение определит фронтальные проекции 324 2 искомых точек. При наличии профильной проекции, точки 32 и 42 могут быть получены непосредственным проецированием с использованием точек 33 и 43.
При построении линии пересечения цилиндра и конуса, оси которых пересекаются в точке О (рис. 81), прежде всего отмечают фронтальные проекции 12 и 22 крайних левой и правой точек линии пересечения; затем находят фронтальные проекции З1 и 42 нижних точек кривой. Для их определения проводят из центра O2 окружность, являющуюся фронтальной проекцией шара, вписанного в цилиндр. Касание шара к цилиндру произойдет по окружности, фронтальная проекция которой изобразится прямой, проходящей через точку O2. С конусом шар пересечется по окружности, параллельной основанию конуса; фронтальная проекция этой окружности спроецируется в прямую, перпендикулярную к первой прямой; их пересечение определит фронтальные проекции 324 2 искомых точек. При наличии профильной проекции, точки 32 и 42 могут быть получены непосредственным проецированием с использованием точек 33 и 43.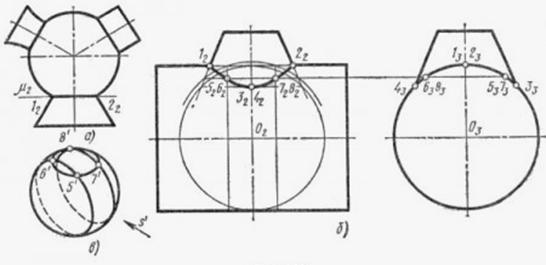
 Если оси пересекающихся поверхностей не параллельны плоскости, то можно воспользоваться методом вращения. Для этого нужно повернуть обе поверхности так, чтобы оси их стали параллельными плоскости проекций, построить линию пересечения и обратным вращением перенести ее на свое место. Можно для решения применить способ перемены плоскостей проекций. Встречаются случаи, когда поверхности вращения пересекаются по двум плоским кривым - эллипсам. Это бывает тогда, когда поверхности двух тел вращения описаны около сфер. Если оси тел вращения параллельны плоскости П2, то фронтальные проекции линии пересечения выявляются отрезками прямых. Если через любую из двух полученных линий пересечения провести фронтально - проектирующую плоскость, то в сечении получим эллипс, его большая ось будет равна отрезку A2В2 или C2D2 (рис.82)
Если оси пересекающихся поверхностей не параллельны плоскости, то можно воспользоваться методом вращения. Для этого нужно повернуть обе поверхности так, чтобы оси их стали параллельными плоскости проекций, построить линию пересечения и обратным вращением перенести ее на свое место. Можно для решения применить способ перемены плоскостей проекций. Встречаются случаи, когда поверхности вращения пересекаются по двум плоским кривым - эллипсам. Это бывает тогда, когда поверхности двух тел вращения описаны около сфер. Если оси тел вращения параллельны плоскости П2, то фронтальные проекции линии пересечения выявляются отрезками прямых. Если через любую из двух полученных линий пересечения провести фронтально - проектирующую плоскость, то в сечении получим эллипс, его большая ось будет равна отрезку A2В2 или C2D2 (рис.82)
