Метод проекций с числовыми отметками получил широкое применение при проектировании сооружений из земли: железных и шоссейных дорог, гидроузлов, каналов, аэродромов, строительных площадок, т. е. в тех случаях, когда высота объекта существенно меньше его длины или ширины. Метод проекций с числовыми отметками является частным случаем ортогональных проекций.
Тема 5-1. План вертикальной планировки. Плоскость нулевого уровня. Градуирование прямой. Заложение отрезка. Уклон
Вертикальная планировка - это инженерное мероприятие по искусственному изменению, преобразованию и улучшению существующего рельефа местности срезкой или подсыпкой грунта для использования его в градостроительных целях. Основная цель вертикальной планировки заключается в создании спланированных поверхностей, удовлетворяющих требованиям застройки и инженерного благоустройства территории.
Вертикальная планировка территории призвана создать благоприятные условия для размещения зданий и сооружений, прокладки улиц, проездов, подземных инженерных коммуникаций. К основным задачам вертикальной планировки относятся:
- организация стока поверхностных вод (дождевых, ливневых и талых) с городских территорий; - обеспечение допустимых уклонов улиц, площадей и перекрёстков для безопасного и удобного движения всех видов городского транспорта и пешеходов;
- создание благоприятных условий для размещения зданий и прокладки подземных инженерных сетей;
- организация рельефа при наличии неблагоприятных физико-геологических процессов (затопление территории, подтопление её грунтовыми водами, оврагообразование и т. д.);
- придание рельефу наибольшей архитектурной выразительности; - создание в необходимых случаях искусственного рельефа;
- решение задач при сооружении крупных и уникальных плоскостных сооружений (спортивного центра, аэродрома и пр.).
Этапы разработки вертикальной планировки заключаются в оценке рельефа, составлении схемы вертикальной планировки в зависимости от площади и сложности рельефа, на основании которых на местности производят геодезические разбивочные работы для преобразования рельефа.
Отметки планируемой поверхности назначают таким образом, чтобы максимально сохранить существующий рельеф, зелёные насаждения и почвенный покров.
При проектировании земляных сооружений необходимо решить комплекс задач на построение проходящей через заданную линию поверхности уклона и на построение линии пересечения поверхностей.
Сущность метода заключается в том, что вместо двух ортогональных проекций объекта (на плоскостях П 1 и П 2) изображают одну, чаще всего горизонтальную проекцию, лежащую в плоскости XOY, и рядом с проекцией каждой точки предмета указывают ее отметку (число), определяющую расстояние (обычно в метрах) от точки до плоскости XOY (координата Z). Плоскость XOY называют плоскостью нулевого уровня и обозначают П 0.
При изображении топографической поверхности за такую плоскость принимают поверхность уровня моря. Точки, расположенные на плоскости нулевого уровня, имеют отрицательные отметки и на чертеже проставляются со знаком минус. Точки, принадлежащие плоскости П 0, имеют нулевую отметку. Проекция с числовой отметкой является обратимым чертежом, поскольку есть возможность восстановить все три параметра точки, расположенной в пространстве.
Чертежи, выполненные в проекциях с числовыми отметками, принято называть планами, на которых показывают линейный масштаб, необходимый для решения метрических задач.
План должен быть определенным образом ориентирован относительно сторон света, на нем в виде стрелки с пометками «С», «Ю» (север, юг) показывают расположение меридиана. Если боковая линия рамки чертежа совпадает с положением меридиана, его можно специально не обозначать.
Рассмотрим основные понятия и построения, связанные с изображениями в проекциях с числовыми отметками прямой, плоскости, поверхности.
Проекции прямой. Для изображения отрезка прямой АВ в проекциях с числовыми отметками показывают проекции двух ее точек А и В.
Длину проекции отрезка А 2 В 5 = L называют заложением прямой. Разность расстояний до плоскости П 0 концов отрезка АВ = (hВ - hА) называют превышением прямой. Отношение превышения прямой к ее заложению называют уклоном прямой: i = (hВ - hА)/L. Численно уклон равен tga, где α - угол наклона прямой к плоскости П0. Уклоны выражают в виде простого отношения - 1:1, 1:2 и т. д., в виде процентов -10%, 20% и т. д. или в виде тысячных — 10%, 20% и т. д.
Длина заложения отрезка прямой, у которого превышение равно единице длины, называется интервалом прямой. Чтобы получить интервал, нужно заложение прямой разделить на ее превышение, l = L/(hВ - hА), где l -интервал прямой. Между уклоном прямой и ее интервалом обратная зависимость, т. е. l = 1/ i и i = 1/ l.
Тема 5-2. Плоскости и поверхности. Горизонтали. Масштаб «падения» плоскости. Построение проекций поверхностей.
Положение плоскости в пространстве в проекциях с числовыми отметками можно задать теми же способами, что и в ортогональных проекциях. Но в проекциях с числовыми отметками плоскость удобнее задавать масштабом ее падения (уклона).
Масштабом падения (уклона) плоскости называют градуированную проекцию линии наибольшего ската (уклона) плоскости.
Масштаб падения на чертеже изображают двумя параллельными прямыми (толстой и тонкой) и обозначают той же буквой, что и плоскость, но с индексом i, например ai. Масштаб падения перпендикулярен проекциям горизонталей плоскости. Расстояние l между проекциями соседних горизонталей, разность отметок которых равна единице, называется интервалом плоскости. Он так же, как и для прямой - величина, обратная уклону плоскости, т. е. l = 1/i = 1/tga.
Масштаб уклона можно построить, если плоскость задана каким-либо другим способом.
Например, на рис.84 плоскость задана проекциями а5;b 2:, с7 точек А, В,С. Соединяют точки b 2 c7 прямой и градуируют ее. Через точку а5 и точку с отметкой 5 на прямой проводят прямую, которая будет горизонталью искомой плоскости с отметкой 5. Остальные горизонтали плоскости будут ей параллельны и пойдут через точки с отметками 4, 3, 2,..., отмеченные на прямой ВС. Масштаб уклона плоскости Рi, проводят перпендикулярно горизонталям плоскости.
Проекции поверхности. Применяя метод проекций с числовыми отметками для изображения геометрических тел (фигур), следует на их горизонтальных проекциях указывать отметки характерных точек или линии. Такими точками в случае многогранника будут его вершины.
Если же тело ограничено кривой поверхностью, то его изображают горизонталями, образующимися в результате пересечения заданной поверхности рядом плоскостей, параллельных плоскости П 0 и отстоящих друг от друга на расстояние, равное единице длины.
Расстояние между этими плоскостями называется высотой сечения горизонталей. Выбирают ее в зависимости от масштаба чертежа и рельефа местности. Высоту сечения нужно указывать на чертеже.
Рис.84. Задание плоскости точками
На рис.85 показано изображение в проекциях с числовыми отметками прямого кругового конуса. Проекции его горизонталей – концентрические окружности, расстояния между которыми равны интервалу l образующей конуса.
Рис.85. Изображение прямого кругового конуса
В некоторых же случаях проведение горизонталей поверхности требует специальных построений. Примером этого может служить поверхность одинакового ската, представляющую собой огибающую семейства прямых круговых конусов с вертикальными осями. Такое семейство образует в пространстве конус, вершина которого перемещается по некоторой пространственной кривой АВ, а ось при движении конуса сохраняет вертикальное положение (рис. 86).
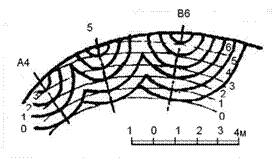
Огибающая такого семейства конусов будет линейчатая поверхность, все прямолинейные образующие которой составляют с П 0 образующих конуса. Построение горизонталей поверхности одинакового ската выполнено на рис.86, где каждая горизонталь поверхности представляет собой огибающую семейства горизонталей конусов.
Причем, все горизонтали конусов данного семейства должны иметь одинаковую отметку. Так, на рис.87 горизонталь поверхности с отметкой 3 огибает семейство горизонталей конусов с той же отметкой 3.
Рис. 86. Построение горизонталей поверхности одинакового ската
Одним из примеров применения этой поверхности в строительной технике являются откосы насыпи из выемки шоссейных или железных дорог.
Все строительные объекты располагаются на земной поверхности, врезаясь или надстраивая рельеф. Поэтому при проектировании строительных объектов и работ необходимо иметь чертеж земной поверхности.
Рис. 87. Горизонтали конусов с одинаковой отметкой
Земную поверхность называют топографической поверхностью. Образование форм отдельных элементов рельефа и их бесконечно-разнообразных сочетаний не может быть описано и задано математически (с помощью уравнений) и поэтому топографическую поверхность рассматривают как особый вид графических поверхностей, задаваемых только изображениями.
Топографическая поверхность (естественная поверхность земли) имеет неправильную форму, поэтому ее горизонтали – кривые линии неправильной формы. На рис. 88 схематично изображен холм, горизонталями которого будут линии пересечения его поверхности с горизонтальными плоскостями П 1, П 2 и т. д. В практике горизонтали топографической поверхности проводят через проекции точек, имеющих одинаковые отметки, определенные в процессе геодезической съемки местности. При решении учебных задач горизонтали топографической поверхности заданы.
Рис. 88. Топографическая поверхность
Помимо числовых отметок при изображении поверхности земли пользуются бергштрихами, указывающими направление ската поверхности. В случае вершины бергштрихи ставятся на одной из верхних горизонталей в сторону ската воды. В котловине концы бергштрихов направлены внутрь нижней горизонтали.
Тема 5-3. Проектирование горизонтальной площадки по заданной геодезической подоснове
Прямая и плоскость.
На рис.89 показано построение линии пересечения плоскостей a и b. Такая задача может встретиться при определении линии пересечения плоских откосов насыпей или выемок. Искомая проекция линии пересечения А 4 В 2 плоскостей a и b проходит через точки пересечения двух пар «одноименных» (с одинаковыми отметками) горизонталей заданных плоскостей.
У параллельных плоскостей в проекциях с числовыми отметками:
-параллельны масштабы уклонов;
-равны интервалы;
-отметки возрастают в одну сторону.
Рис.89. Построение линии пересечения плоскостей а и b.
Плоскость и поверхность.
Линия пересечения плоскости с поверхностью конуса будет проходить через точки пересечения одноименных горизонталей этих поверхностей. Решение этой задачи также встречается в практике строительного проектирования, поскольку откосы насыпей или выемок могут иметь коническую форму. На рис.90 показан пример решения такой задачи. Проекция линии пересечения конической поверхности с плоскостью a проходит через точки А 1, В 2, С 3, D 4.
Рис.90. Построение линии пересечения плоскости с поверхностью конуса
Рис. 91. Построение линии пересечения поверхности с горизонтально проецирующей плоскостью
Линия пересечения топографической поверхности с горизонтально проецирующей плоскостью b (рис. 91) носит название профиля топографической поверхности Построение этой линии - распространенная в строительном проектировании задача. Для решения ее рекомендуется следующий практический прием. К проекции плоскости b, ее горизонтальному следу b¢, прикладывают полоску бумаги, куда переносят точки пересечения плоскости с горизонталями топографической поверхности А 3,B 4,С 5,D 6,Е 7,f 8. Полученные точки переносят на горизонтальную линию - основание профиля, отметку которой задают условно (обычно эта отметка является минимальной). В данном случае отметка основания 3,00. Затем в масштабе чертежа из отмеченных точек откладывают по перпендикуляру вверх превышения отмеченных точек (разность отметки точки и принятой отметки основания профиля). Искомая линия профиля (сечения плоскости с топографической поверхностью) будет проходить через точки А,В,С,D,E,F.
Решение инженерных задач. Как указывалось выше, проекции с числовыми отметками используют для изображения инженерных сооружений из земли. Чтобы определить объемы и размеры земляных работ, находят линии пересечения откосов насыпей или выемок с поверхностью местности. Иными словами, строят линию пересечения поверхности откоса (плоскости, конуса, поверхности одинакового ската) с топографической поверхностью. Искомую линию в таком случае определяют рядом точек пересечения искомых точек пересечения одноименных (с одноименными отметками) горизонталей топографической поверхности и поверхности откоса.
Методика решения задач. На рис.92 заданы топографическая поверхность и горизонтальный участок полотна дороги, отметка которого 12,00 м. Дорога будет расположена на насыпи, так как отметки горизонталей местности (топографической поверхности) меньше отметки полотна дороги. Требуется определить границы насыпи дороги.
Рис. 92. Топографическая поверхность
Уклон откосов насыпи задан и равен 1:1,5, поэтому интервал плоскостей откосов насыпи будет равен 1 м. Граница насыпи пройдет через точки пересечения одноименных горизонталей откосов насыпи и топографической поверхности. Проводим параллельно бровке дороги горизонтали плоскости южного откоса насыпи и отмечаем точки А11, А10, С9, D8, E7, через которые проходит искомая линия. Аналогично строят линию пересечения топографической поверхности с северным откосом насыпи.
Пример решения задачи на рис. 93, на котором заданы топографическая поверхность и расположенная на ней горизонтальная строительная площадка с отметкой 22, а также наклонный въезд на площадку (аппарель). Заданы уклоны насыпи 1:1,5, выемки 1:2 и дороги (аппарели) 1:5.
Проекции горизонталей плоских откосов площадок будут прямые, параллельные ее бровке и отстоящие друг от друга на 1,5 м для насыпи и на 2 м для выемки. Построение линий пересечения их с топографической поверхностью сводится к решению примера, рассмотренного на рис. 92.
Поверхность выемки, примыкающей к криволинейной части площадки, будет конической, а горизонтали откоса этой части выемки - концентрическими окружностями, расстояния между которыми (интервалы) равны 2 м. Построение линии пересечения конического откоса с топографической поверхностью показано на рис. 87.
Аппарель (наклонный въезд на площадку) имеет уклон, горизонтали аппарели будут расположены на расстоянии 5 м друг от друга, а горизонтали откосов насыпи аппарели будут касательные к горизонталям конусов, имеющих вершины на бровке аппарели.
Профиль местности строят аналогично примеру, рассмотренному на рис. 91. На профиле показывают попавшие в секущую плоскость контуры горизонтальной площадки, наклонной дороги и откосов насыпи и выемки.
Последовательность решения. Пусть задача сформулирована так. Построить контуры строительной площадки и участка дороги в проекциях с числовыми отметками.
Пример решения задачи для студентов показан на рис.94. Задана топографическая поверхность (рис. 93) и полотно дороги с горизонтальным криволинейным участком и отметкой 22.
Решая инженерную задачу, необходимо выполнить следующие подготовительные и чертежно-графические операции.
1. Ознакомиться с содержанием задачи.
2. Выбрать и изучить метод решения.
3. Подготовить формат A3 (начертить рамку, основную надпись).
4. Над основной надписью изобразить линейный масштаб чертежа М1:200.
5. Разметить положение горизонталей рельефа местности в соответствии с рис.93.
6. Используя линейный масштаб, над основной надписью построить график масштабов уклонов насыпи - i н = 1:1,5; выемки - i в = 1:1 и аппарели i а = 1:6 в виде их профиля
7. Определить точки нулевых работ как точки пересечения горизонтали местности с одноименной отметкой с контуром строительной площадки или дороги. Также определить места расположения насыпей и выемок.
9. Построить масштабы уклонов плоскостей откосов насыпей, выемок, обозначить числовые отметки.
10. Построить горизонтали аппарели, откосов и линии их пересечения.
11. Определить точки пересечения горизонталей топографической поверхности с горизонталями откосов, построить границы откосов насыпей и выемок.
12. По направлению ската воды откоса изобразить бергштрихи.
13. Обвести линии пересечения откосов насыпей и выемок с топографической поверхностью.
14. В нижней части формата слева от основной надписи построить профиль строительной площадки или дороги в соответствии с вариантом положения секущей плоскости.
15. Оформить эпюр.
На рис. 93 задан план местности в горизонталях и проектируемой на этом участке местности горизонтальной площадки и выезда из нее справа. Площадка имеет форму прямоугольника с примыкающим к нему полукругом.
Заданы уклон дороги (выезда), уклон откосов насыпей 1: 1,5 и уклон откосов выемок 1:1, уклон аппарели 1:6. Выделенную на чертеже горизонталь с отметкой 22 называется линией нулевых работ - она отделяет зону выемки от зоны насыпи.
Горизонтали откосов насыпи, граничащих с дорогой, строятся при помощи конусов после того, как предварительно построены горизонтали дороги.
Рис. 93. План местности в горизонталях и проектируемая площадка
Откосы насыпи и выемки, граничащие с круглыми краями площадки и канавы, имеют форму конусов вращения, а их горизонтали в плане концентрические окружности.
Затем строятся линии пересечения соседних откосов друг с другом и всех откосов с землей – в основном по точкам пересечения одноименных горизонталей, т.е. с помощью горизонтальных вспомогательных горизонтальных плоскостей.
Для более точного построения линий пересечения с землей откосов насыпи, примыкающих к правому краю площадки, можно применить вспомогательные плоскости общего положения. Линия пересечения плоского и конического откосов насыпи – парабола, поскольку плоскость и конус имеют одинаковый уклон, т.е. плоскость параллельна одной из образующих конуса.
Смежные плоский и конический откосы выемки переходят друг в друга плавно, т.е. не пересекаются, а касаются.
Линии пересечения двух откосов друг с другом и две линии пересечения этих откосов с землей сходятся в одной точке этих трех поверхностей.
После определения границ всех откосов на каждом из них наносятся бергштрихи (параллельные длинные и короткие штрихи), которые показывают направление стока воды по откосу. Они начинаются от верхнего края откоса и направлены по его линиям наибольшего ската, т.е. перпендикулярно его горизонталям.
Затем выполняется построение разреза А-А. Плоскость А-А пересекает откос насыпи, примыкающий к площадке, откос, примыкающий к дороге, дорогу, горизонтальную площадку, еще один плоский откос и конический откос.
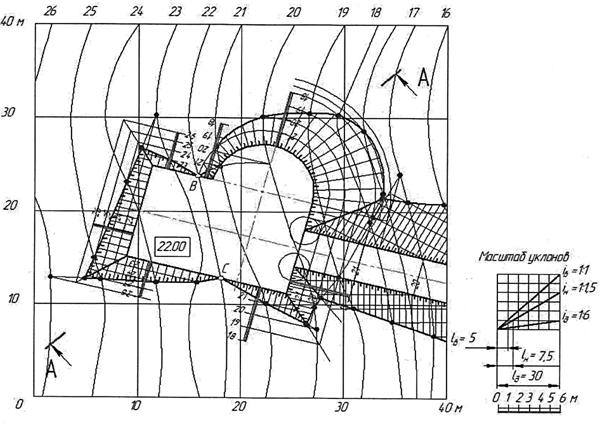
Рис. 94. Вариант спроектированной горизонтальной площадки с дорогой.
Построение продольного уклона дороги.
Рис. 95. Пример построения уклона дороги
Продольный уклон дороги i≠0, уклон откоса насыпи iн=1:1,5. Плоскость дорожного полотна градуируется. Откос дорожного полотна градуируется следующим образом. В точке с вершиной 50,00 (или другой точке) помещаем вершину конуса, описываем окружность радиусом, равным интервалу откоса насыпи (в нашем примере l = 1,5м). Отметка этой горизонтали конуса будет на единицу меньше отметки вершины, т.е. 49м. Проводим ряд окружностей, получаем отметки горизонталей 48, 47, касательно к которым из точек бровки с отметками 49, 48, 47 проводим горизонтали откоса насыпи.
Литература
Основная литература
1. Боголюбов С.К. Начертательная геометрия и инженерная графика, учебник, 3-е изд. испр. и дополн., М., Машиностроение, 2006, 352 с.,ил.
2. Единая система конструкторской документации (ЕСКД), полное собрание ГОСТ с 2.301 по 2.321, М., Издательство стандартов, 2004, 160 с.
3. Короев Ю.И. Начертательная геометрия, учебник для студентов ВУЗов стр. спец., М., Высшая школа, 2009, 454 с., ил.
4. Павлова А.А. начертательная геометрия, учебник, М., Молодая гвардия, 2009, 252 с., ил.
5. Соловьев С.А., Буланже Г.В., Шульга А.К. Черчение и перспектива, учебник для ССУЗов, М., Просвещение, 2010, 324 с., ил.
6. Чекмарев А.А. Начертательная геометрия и черчение, учебник для студентов ВУЗов, М., ВЛАДОС, 2010, 471с., ил.
Дополнительная литература
1. Золотарев С.В., Кошелева Е.Д. Инженерная графика, учебное пособие, М., Издательство РГАУ – МСХА имени К.А. Тимирязева, 2011, 84 с., ил.
2. Иванов Г.С. Начертательная геометрия, учебное пособие, М., Высшая Школа, 2009, 72 с., ил.
Методические указания и рекомендации
1. Кудринская Н.П. Начертательная геометрия, сборник заданий, М., Издательство РГАУ – МСХА имени К.А. Тимирязева, 2010, 69 с., ил.
2. Миронов В.И. Начертательная геометрия. Методические указания и контрольные задания, М., Издательство РГАУ-МСХА им. К.А. Тимирязева, 2013, 52 с., ил.
3. Фролов С.А. и др. Начертательная геометрия и инженерная графика, методические указания и контрольные задания, Тверь, Издательство ТГСХА, 2009,34 с., ил.
Программное обеспечение и Интернет – ресурсы
1. Программа по начертательной геометрии A9CAD 2.2.1
2. Программа по начертательной геометрии и черчению G Star CAD
3. Программа по начертательной геометрии и черчению ZWCAD
Интернет ресурсы
1. Сайт ing – grafika.ru
2. Сайт kodges.ru/33537 – nachertatelnaja
3. Сайт studdraw. narod.ru
Учебное издание
Миронов Владимир Иванович
