Тема 3-1. Цилиндрическиеповерхности. Прямоугольные проекции. Аксонометрия. Развертка цилиндра. Сечение цилиндра плоскостями
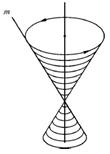
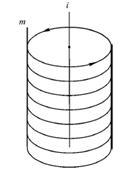 Цилиндр – это фигура, поверхность которого получается вращением прямой m вокруг оси i, расположенной в одной плоскости с этой прямой. В случае, когда прямая m направлена параллельно оси вращения, получается цилиндр (рис.58), когда она пересекает ось вращения, полученная фигура будет являться конусом (рис.59). Прямой круговой цилиндр имеет образующие, направленные перпендикулярно горизонтальной плоскости.
Цилиндр – это фигура, поверхность которого получается вращением прямой m вокруг оси i, расположенной в одной плоскости с этой прямой. В случае, когда прямая m направлена параллельно оси вращения, получается цилиндр (рис.58), когда она пересекает ось вращения, полученная фигура будет являться конусом (рис.59). Прямой круговой цилиндр имеет образующие, направленные перпендикулярно горизонтальной плоскости.
Рис.58. Цилиндр Рис.59. Конус
 Рис. 60. Проекции прямого кругового цилиндра и точки на его боковой поверхности.
Рис. 60. Проекции прямого кругового цилиндра и точки на его боковой поверхности.
 Рассмотрим горизонтальную проекцию цилиндра. Если провести фронтальную плоскость Р, разделяющую цилиндр на две равные части, можно заметить, что все точки, лежащие на передней половине цилиндра, будут видны при рассмотрении цилиндра спереди. Для выделения невидимых элементов на профильной проекции, необходимо обратиться к горизонтальной проекции.
Рассмотрим горизонтальную проекцию цилиндра. Если провести фронтальную плоскость Р, разделяющую цилиндр на две равные части, можно заметить, что все точки, лежащие на передней половине цилиндра, будут видны при рассмотрении цилиндра спереди. Для выделения невидимых элементов на профильной проекции, необходимо обратиться к горизонтальной проекции.
Построение развертки цилиндра начинают с деления поверхности цилиндра на определенное количество равных частей, например на 12, и развертывают вписанную поверхность правильной двенадцатиугольной призмы. Длина развертки при таком построении получается несколько меньше действительной длины развертки.
Рис. 61. Построение развертки цилиндра
Сечение цилиндра плоскостями
 При пересечении поверхности вращения плоскостью получается плоская фигура сечения. Построение проекций линии сечения необходимо начинать с определения опорных точек. К ним относятся точки, расположенные на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой), и точки, удаленные на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные (промежуточные) точки линии сечения.
Для определения точек, принадлежащих фигуре сечения, можно использовать различные методы. Один из них - метод вспомогательных секущих плоскостей. Суть его заключается в том, что заданные плоскость и поверхность вращения пересекают вспомогательной плоскостью. Сначала находят линии пересечения этой плоскости с заданными плоскостью и поверхностью вращения. Затем отмечают точки, в которых пересекаются полученные линии пересечения. Построенные точки фигуры сечения соединяют плавной линией.
Рис.62. Сечение цилиндра фронтально – проецирующей плоскостью:
а) прямоугольные проекции, б) развертка, в) аксонометрия. При пересечении поверхности вращения плоскостью получается плоская фигура сечения. Построение проекций линии сечения необходимо начинать с определения опорных точек. К ним относятся точки, расположенные на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой), и точки, удаленные на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные (промежуточные) точки линии сечения.
Для определения точек, принадлежащих фигуре сечения, можно использовать различные методы. Один из них - метод вспомогательных секущих плоскостей. Суть его заключается в том, что заданные плоскость и поверхность вращения пересекают вспомогательной плоскостью. Сначала находят линии пересечения этой плоскости с заданными плоскостью и поверхностью вращения. Затем отмечают точки, в которых пересекаются полученные линии пересечения. Построенные точки фигуры сечения соединяют плавной линией.
Рис.62. Сечение цилиндра фронтально – проецирующей плоскостью:
а) прямоугольные проекции, б) развертка, в) аксонометрия.
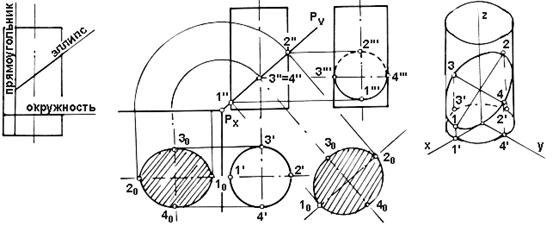 Рис. 63. Сечение цилиндра плоскостью общего положения
Тема 3-2. Конические поверхности. Развертка. Сечение конуса плоскостями. Пересечение конуса с прямой Рис. 63. Сечение цилиндра плоскостью общего положения
Тема 3-2. Конические поверхности. Развертка. Сечение конуса плоскостями. Пересечение конуса с прямой
Рис. 64. Прямой круговой конус Боковая поверхность конуса получается при вращении образующей вокруг оси конуса по направляющей - окружности основания. Если на поверхности конуса задана одна проекция точки А (например, фронтальная проекция на рис. 65, а), то две другие проекции этой точки определяют с помощью вспомогательных линий - образующей, расположенной на поверхности конуса и проведенной через точку А, или окружности, расположенной в плоскости, параллельной основанию конуса. В первом случае (рис. 65, а) проводят фронтальную проекцию s'a'f вспомогательной образующей. Пользуясь вертикальной линией связи, проведенной из точки /, расположенной на фронтальной проекции окружности основания, находят горизонтальную проекцию sf этой образующей, на которой при помощи линии связи, проходящей через а', находят искомую точку а. Во втором случае (рис. 65, б) вспомогательной линией, проходящей через точку А, будет окружность, расположенная на конической поверхности и параллельная плоскости Н. Фронтальная проекция этой окружности изображается в виде отрезка b 'с' горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция а точки А находится на пересечении линии связи, опущенной из точки а', с горизонтальной проекцией вспомогательной окружности. Если заданная фронтальная проекция b ' точки В расположена на контурной (очерковой) образующей SK, то горизонтальная проекция точки находится без вспомогательных линий. В изометрической проекции точку А, находящуюся на поверхности конуса, строят по трем координатам: xA = N, yA = M, zA = H. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям.
Рис. 65. Проекции конуса Развертку конуса вращения строят так же, как и развертку пирамиды. Делят окружность основания на равные части, например на 12 частей, и представляют, что в конус вписана правильная двенадцатиугольная пирамида. Как известно из геометрии, развертка конуса изображается сектором круга, у которого радиус равен длине образующей конуса L. Все образующие кругового конуса равны, поэтому действительная длина образующей L равна фронтальной проекции левой (или правой) образующей. Угол φ = 360°. Снизу пристраивают основание конуса.
Пересечение конуса с прямой
|
Рис. 67. Нахождение следов прямой на поверхности конуса
Тогда найдём проекции точек пересечения (рис.67, а):
1) плоскость Р определяется точкой S и прямой I, тогда найдем ее след Р h. При этом одна точка следа P h определяется следом h 1 прямой I. Вторая точка искомого следа P h находится путем проведения в плоскости Р произвольной прямой до встречи с горизонтальной плоскостью. С этой целью соединим точку S с любой точкой С этой прямой и найдем след h 2 прямой SC. Прямая, соединяющая точки h 1 и h 2, будет представлять собой след P h;
2) затем нужно приступать к нахождению горизонтальных проекций а и b точек пересечения А и В следа P h с окружностью основания конуса;
3) после этого проводят горизонтальные проекции as и bs, образующих AS и BS, причем их фронтальные проекции не нужны;
4) далее отмечают точки пересечения m и n горизонтальных проекций образующих as и bs с горизонтальной проекцией данной прямой, они будут горизонтальными проекциями искомых точек М и N;
5) в заключение остается найти фронтальные проекции ḿ и ń на фронтальной проекции Í данной прямой.
Сечение конуса плоскостями
Поверхность прямого кругового конуса относительна к поверхностям вращения и является носителем кривых второго порядка: окружности, эллипса, параболы и гиперболы. Все эти кривые являются плоскими и, следовательно, могут быть получены в результате сечения конической поверхности плоскостью.

Рис. 68.Различные случаи сечения поверхности
Кругового конуса плоскостью:
а) гипербола; б) эллипс; в) парабола
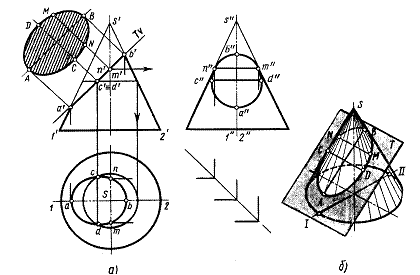
Рис. 69. Сечение конуса фронтально – проецирующей плоскостью: а) прямоугольные проекции, б) аксонометрия.

Рис.70. Сечение конуса плоскостью общего положения.
Тема 3 - 3. Сферические поверхности. Виды сферических поверхностей. Сечение сфер плоскостями. Пересечение сферы с прямой линией
Сферическая поверхность– это геометрическое место точек (т.е. множество всех точек) в пространстве, равноудалённых от одной точки O, которая называется центром сферической поверхности. Радиус AO и диаметр AB определяются так же, как и в окружности (рис.71).

Рис. 71. Сферическая поверхность
Шар (сфера) - это тело, ограниченное сферической поверхностью. Можно получить шар, вращая полукруг (или круг) вокруг диаметра. Все плоские сечения шара – круги (рис.71). Наибольший круг лежит в сечении, проходящем через центр шара, и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара (AB, рис.71). Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (A и B, рис.71), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов
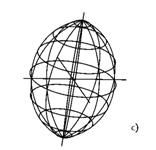
Рис. 72. Эллипсоид
Поверхность вращения общего вида образуется вращательным перемещением образующей линии вокруг неподвижной оси. Каждая точка образующей линии при вращении вокруг неподвижной оси описывает окружность с центром на оси вращения. Эти окружности называются параллелями.

 Наибольшую из параллелей (окружностей) поверхности вращения называют экватором поверхности, а наименьшую - горлом (шейкой) поверхности. Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, - меридианами. Меридиональная плоскость, параллельная плоскости проекции, называется плоскостью главного меридиана.
Наибольшую из параллелей (окружностей) поверхности вращения называют экватором поверхности, а наименьшую - горлом (шейкой) поверхности. Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, - меридианами. Меридиональная плоскость, параллельная плоскости проекции, называется плоскостью главного меридиана.
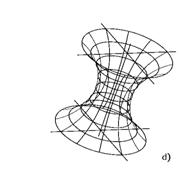
 В зависимости от вида вращающейся образующей, различают: торовые поверхности (образуется вращением окружности или дуги окружности).
В зависимости от вида вращающейся образующей, различают: торовые поверхности (образуется вращением окружности или дуги окружности).
Рис. 73. Торовые поверхности: а-сфера; б-открытый тор; с-закрытый тор; d-глобоид.
Сечения сфер плоскостями
Плоскость Т пересекает шар по окружности. Так как плоскость Т не является плоскостью уровня, то на всех проекциях окружность проецируется или в отрезок прямой, или в эллипсы, построение которых сводится к определению центров эллипсов и их сопряженных диаметров.
Центр окружности лежит на середине отрезка 1-2,так как отрезок 1-2 есть н.в. окружности. Поэтому н.в. сечения будет окружность с Æ = 1-2. Эллипс 1'-2'-3'-4' на Н определяется своими осями 3-4, 1-2, причем ось 3-4, являясь отрезком фронтально-проецирующей прямой, проецируется на плоскость Н в натуральную величину. Точки 7, 8 эллипса, лежащие на экваторе, определяют видимость эллипса на плоскости Н.

Рис. 74. Сечение шара плоскостью общего положения
Пересечение сферы с прямой
Задачи на пересечение прямой с поверхностью решаются аналогично задачам на пересечение прямой с плоскостью и многогранником:
- через прямую проводится вспомогательная плоскость;

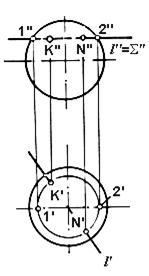 - находится линия пересечения поверхности с введенной плоскостью;
- находится линия пересечения поверхности с введенной плоскостью;
- определяются точки пересечения заданной прямой с найденной линией;
- определяется видимость прямой.
При решении задачи на пересечение прямой с поверхностью важно выбрать вспомогательную плоскость: ту, которая дает простое сечение - окружность или прямоугольник.
Рис. 75. Пересечение сферы с прямой
В тех случаях, когда вспомогательная плоскость рассекает поверхность по простой фигуре, но на проекциях получается более сложная, используется замена плоскостей проекций и, когда выгодно делается замена так, чтобы прямая стала проецирующей, в этом случае задача решается на принадлежность точки поверхности.





 Круговой конус - это тело, состоящее из круга (основание конуса), точки, которая не лежит в плоскости этого круга (вершина конуса и всех отрезков, которые соединяют вершину конуса с точками основания). Отрезки, которые соединяют вершину конуса и точки окружности основания, называют образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.
Прямой конус – это конус, в котором прямая, которая соединяет вершину конуса и центр основания, перпендикулярна плоскости основания.
Прямой круговой конус – это тело, которое получено вращением прямоугольного треугольника вокруг его катета как оси.
Круговой конус - это тело, состоящее из круга (основание конуса), точки, которая не лежит в плоскости этого круга (вершина конуса и всех отрезков, которые соединяют вершину конуса с точками основания). Отрезки, которые соединяют вершину конуса и точки окружности основания, называют образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.
Прямой конус – это конус, в котором прямая, которая соединяет вершину конуса и центр основания, перпендикулярна плоскости основания.
Прямой круговой конус – это тело, которое получено вращением прямоугольного треугольника вокруг его катета как оси.

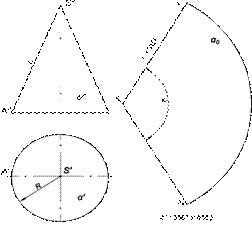 Рис.66. Построение развертки конус
Рис.66. Построение развертки конус Пусть нужно найти точки М и N, в которых прямая I встречает поверхность конуса. Для этого рассмотрим рис. 67, на котором показано нахождение следов прямой на поверхности конуса. Через вершину S и данную прямую I проводят плоскость Р, что показано на рисунке 67, б, причем плоскость Р будет пересекать конус по двум образующим: AS и BS. Упомянутые образующие встретят данную прямую в искомых точках М и N.
Пусть нужно найти точки М и N, в которых прямая I встречает поверхность конуса. Для этого рассмотрим рис. 67, на котором показано нахождение следов прямой на поверхности конуса. Через вершину S и данную прямую I проводят плоскость Р, что показано на рисунке 67, б, причем плоскость Р будет пересекать конус по двум образующим: AS и BS. Упомянутые образующие встретят данную прямую в искомых точках М и N.
