МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное Бюджетное образовательное учреждение
высшего образования
«российский государственный аграрный университет –
МСха имени К.А. Тимирязева»
(ФГБОУ ВО ргау - МСХА имени К.А. Тимирязева)
___________________________________________________________________________________
К 150 летию
Тимирязевской академии
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
В ЛАНДШАФТНОЙ АРХИТЕКТУРЕ
Учебное пособие
Москва
Издательство РГАУ-МСХА
2015
УДК 712:514.182(083.131)
ББК 85.118.7:22.151.3я81
М58
Миронов В.И., Рукавишникова Е.Л. Начертательная геометрия в ландшафтной архитектуре: Учебное пособие / В.И.Миронов, Е.Л.Рукавишникова - М.: Изд-во РГАУ-МСХА, 2015, - 101 с.
Материал, представленный в учебном пособии, соответствует учебной программе дисциплины «Начертательная геометрия в ландшафтной архитектуре». Учебное пособие можно использовать для самостоятельного изучения курса, а также при дистанционном обучении.
Предназначено для студентов очной, очно-заочной и заочной форм обучения, обучающихся по направлению 35.03.10 «Ландшафтная архитектура».
Рецензент: кандидат технических наук И.А.Кипнис (ЗАО «Научно-производственная фирма Касиор»)
ISBN 978-5-9675-1309-1 © Миронов В.И., Рукавишникова Е.Л., 2015
© ФГБОУ ВО РГАУ – МСХА
имени К.А.Тимирязева, 2015
© Издательство РГАУ – МСХА, 2015
Содержание
Раздел 1. Введение …………………………………. ……………………………………………………….с.4
Тема 1-1. Общие сведения о чертежах. Графическое оформление чертежей. ГОСТы. Виды чертежей. Форматы чертежей. Рамка и основная надпись. Масштабы. Линии чертежа…………………………….с.5
Тема 1-2. Шрифт чертёжный. Архитектурный шрифт………………………..............................................с.7
Тема 1-3. Геометрические построения. Деление отрезков и углов. Способы
построения многоугольников…………………………………………………………………………………с.10
Тема 1-4. Сопряжения. Архитектурные обломы……………………………………………………………с.10
Раздел 2. Проецирование
Тема 2-1. Центральное и параллельное проецирование. Прямоугольное и косоугольное
проецирование………………………………………………………………………………………………...с.12
Тема 2-2. Метод Монжа. Проецирование точек…………………………………………………………….с.14
Тема 2-3. Проецирование прямых. Прямые общего и частного положения. Взаимное положение
двух прямых……………………………………………………………………………………………………с.15
Тема 2-4. Проецирование плоскостей. Способы задания плоскости на эпюре. Плоскости общего
и частного положения. Взаимное положение двух плоскостей. Пересечение плоскостей. Пересечение плоскости с прямой линией…..……………………………………………………………………………….с.17
Тема 2-5. Многогранники, их изображение на эпюре и в аксонометрии. Развертки многогранников. Пересечение многогранников с прямо линией. Сечения многогранников плоскостями общего и частного положений……………………………………………………………………………………………………..с.31
Раздел 3. Криволинейные поверхности.
Тема 3-1. Цилиндрические поверхности. Прямоугольные проекции. Аксонометрия. Развертка цилиндра. Сечение цилиндра плоскостями...…………………………..………………………………………………с.38
Тема 3-2. Конические поверхности. Развертка. Сечение конуса плоскостями. Пересечение конуса с прямой…………………………………………………………………………………………………………с.40
Тема 3-3. Сферические поверхности. Виды сферических поверхностей. Сечение сфер плоскостями. Пересечение сферы с прямой линией. ………………..…………………………………………………….с.44
Раздел 4. Пересечение геометрических тел.
Тема 4-1. Пересечение многогранников (пирамиды с призмой)…………………………………………с.46
Тема 4-2. Пересечение криволинейных поверхностей с многогранниками …………………………….с. 47
Тема 4-3. Пересечение криволинейных поверхностей с криволинейными поверхностями …………...с. 50
Раздел 5. Проекции с числовыми отметками.
Тема 5-1. План вертикальной планировки. Плоскость нулевого уровня. Градуирование прямой. Заложение отрезка. Уклон……………………………………….…………………………………………..с. 54
Тема 5- 2. Плоскости и поверхности. Горизонтали. Масштаб «падения» плоскости. Построение проекций поверхностей………………………………………………………………………………………………….с.56
Тема 5-3. Проектирование горизонтальной площадки по заданной геодезической подоснове………..с.58
Литература …………………………………………………………………………………………………...с.63
Раздел 1. Введение
Начертательную геометрию бакалавры по направлению 250700.62 «Ландшафтная архитектура» изучают на первом курсе. Перед изучением курса необходимо ознакомиться с учебной программой, приобрести рекомендованную литературу, продумать план самостоятельной работы. Наряду с изучением теоретического курса и аудиторными практическими занятиями требуется самостоятельно выполнить ряд графических и контрольных работ.
Важность изучения дисциплины «Начертательная геометрия» в том, что в процессе освоения ее, у студентов развивается пространственное воображение/мышление, студент обучается «читать» чертежи, а также с помощью чертежа передавать свои мысли и правильно понимать мысли другого.
Дисциплина «Начертательная геометрия» служит основой для последующего изучения таких дисциплин, как «Архитектурная графика и основы композиции», «Ландшафтное проектирование», «Компьютерная графика» и ряда других.
При изучении дисциплины «Начертательная геометрия» предусматривается: лекционное изложение курса, аудиторные практические занятия, работа с учебниками и учебными пособиями, выполнение расчетно–графических и контрольных работ.
На лекциях рассматриваются принципиальные вопросы, формулируются и доказываются основные положения дисциплины, рассматриваются типовые геометрические задачи, разбирается последовательность их решения.
Рассмотрение частных случаев, вариантов построения проводится на аудиторных практических занятиях. Методика практических занятий основывается на активной форме усвоения материала, обеспечивающей максимальную самостоятельность каждого студента в решении задач.
Студенты выполняют ряд комплексных расчетно–графических и контрольных работ с решением позиционных и метрических задач по основным разделам дисциплины.
Завершающим этапом можно считать собеседование по расчетно–графическим работам и защиту контрольных работ для выявления уровня самостоятельности их выполнения. Знания, умения навыки и способности к представлению пространственных форм выявляются на экзамене. К экзамену допускаются студенты, выполнившие все расчетно–графические и контрольные работы.
Тема 1-1. Общие сведения о чертежах Графическое оформление чертежей. ГОСТы. Виды чертежей. Форматы чертежей. Рамка и основная надпись. Линии чертежа
Чертеж – это документ, содержащий изображения зданий, сооружений, объектов «малой» архитектуры и их деталей, элементов ландшафта, а также сведения, необходимые для строительства зданий, сооружений, объектов «малой» архитектуры и ландшафта, изготовления и контроля деталей. Вся конструкторская документация выполняется по правилам, регламентированным Государственными стандартами (ГОСТами). Например, ГОСТ 2.304-81 расшифровывается следующим образом: ГОСТ – Государственный стандарт; 2 – принадлежность данного стандарта к ЕСКД (единой системе конструкторской документации); 3 – порядковый № группы стандартов (в данном случае «Общие сведения о чертежах»); 04 – порядковый № стандарта (в данном случае «Шрифты чертежные»); 81 – год принятия или изменения стандарта.
В архитектурно-строительных чертежах используется также система СПДС–система проектной документации для строительства.
Виды чертежей (ГОСТ 2.102-68)
Оригинал выполняется собственноручно ландшафтным архитектором на чертежной бумаге и предназначен для изготовления по нему подлинников. Подлинник выполняется при помощи графических компьютерных программ, оформляется соответствующими подписями и печатями и предназначен для изготовления с него копий. Копия идентична с подлинником и предназначена для использования на производстве и в строительстве.
Вся проектно-конструкторская документация подразделяется на графическую: чертежи и схемы и текстовую: пояснительные записки, спецификации, экспликации, ассортиментные ведомости, технические условия и т.п.
Форматы чертежей. Рамка и основная надпись
Чертежи выполняют на листах бумаги с определенным соотношением сторон (ГОСТ 2.301-68). Установлены пять основных форматов: А0 (841х1189), площадью 1,0 кв.м., А1(594х841), А2(420х594), А3(297х420) и А4(210х297). Дополнительные форматы образуются по нижеприведенной сетке форматов.


Рис. 1. Форматы чертежей Рис. 2. Оформление чертежа рамкой и основной
надписью (штампиком)
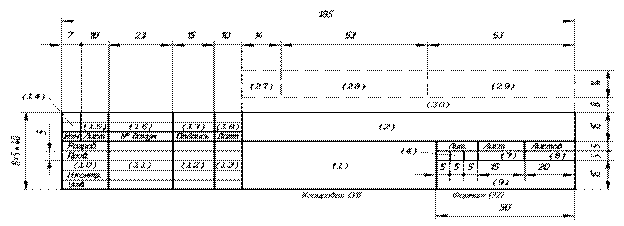
Рис.3. Основная надпись чертежа (штампик)
гpафа 1 - наименование изделия в именительном падеже в единственном числе.
гpафа 2 - обозначение документа по ГОСТ 2.201 - 80.
графа 4 – литера чертежа. На учебных чертежах проставляется заглавная буква У (учебный);
графа 7 - порядковый номер листа;
графа 8 - общее количество листов документа;
графа 9 - наименование или индекс предприятия, выпустившего документ (наименование ВУЗа и группы);
графа 11 – фамилии лиц, подписавших документ;
графа 12 – подписи лиц, фамилии которых указаны в графе 11;
графа 13 – дата подписания документа.
Масштабы
Масштабом называется отношение размеров предмета на чертеже к размерам в натуре. Масштабы могут быть числовыми и графическими. Числовые масштабы бывают: уменьшения, увеличения и натуральная величина. Графические масштабы показаны на рис. 4.
М1:50


Рис.4. Графические масштабы: а) линейный, б) поперечный, в) угловой
Линии чертежа
Чтобы чертеж был выразительным и хорошо читался, он должен быть оформлен линиями различной толщины и начертания. Основная линия чертежа – это линия видимого контура. Толщину сплошной основной линии выбирают в пределах s = 0,5 – 1,4 мм в зависимости от назначения и формата чертежа. Выбранные толщины линий должны бать одинаковыми на данном чертеже. При этом необходимо выдерживать указанные в таблице 1 соотношения толщин линий по отношению к сплошной основной линии, а также их начертание.
Таблица 1. Линии чертежа (ГОСТ 2.303-68)

Тема 1-2. Шрифт чертежный. Архитектурный шрифт
Шрифт – рисунок, начертание букв какого-либо алфавита, цифр, знаков. Первый стандарт «Шрифты для надписей» был разработан в 1919г. Все надписи, которые наносят на чертежи, должны выполняться чертежным шрифтом, установленным по ГОСТ 2.304-81. Стандарт устанавливает и определяет высоту и ширину букв и цифр, толщину линий обводки, расстояние между буквами, словами, строками.
Чертежный шрифт делится на два типа: тип А и тип Б. Тип А и Б различаются параметром h - высота прописных букв в миллиметрах, измеренная по перпендикуляру к основанию строки. Необходимо применять следующие размеры шрифта: (1,8); 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40; шрифт размера 1,8 применяют только к шрифту типа Б.
Шрифты типов А и Б можно применять с наклоном около 75° к основанию строки или без наклона. Основой правильности написания шрифта является вспомогательная сетка, которая образовывается вспомогательными линиями, в которую вписываются буквы.
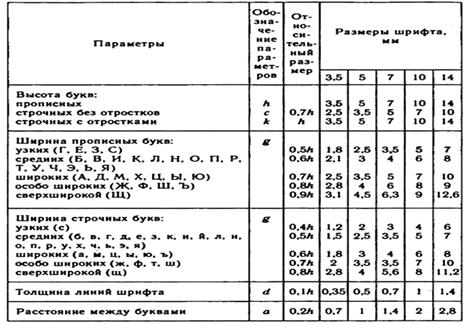 Таблица 2. Размеры букв и цифр по ГОСТ 2.304-68
Таблица 2. Размеры букв и цифр по ГОСТ 2.304-68

Рис. 5. Начертание букв и цифр шрифта чертежного ГОСТ 2.3043-81: прописные буквы, цифры, строчные буквы.
.
Латинские буквы

Прямой шрифт

Таблица 3.
Особенности вычерчивания характерных элементов букв чертежного шрифта

Архитектурный шрифт
 В графическом оформлении любого чертежа важное место занимает правильный выбор шрифта. Расчет надписей, выполненных узким архитектурным шрифтом, очень прост. Расстояние между буквами или пробел в узком архитектурном шрифте один и тот же. Слова одной высоты. Гарнитуры «узкого архитектурного шрифта» вписываются в узкие прямоугольники и площадь между буквами получаете практически одинаковой. Пропорции этого шрифт следующие: S норм = 1/6 Н, где S норм – ширина нормальной буквы, Н - высота буквы, S шир.=1,5S, где S шир. - ширина широких букв, их шесть: Ж, Ф, Ш, Щ, Ы, Ю. Необходимо также отметить, что цифры и буквы на чертеже, имеющие одинаковый размер, должны быть выполнены в одном стиле с хорошими сопряжениями. Радиус сопряжения равен 0,5S. Расстояние между буквами в слове равно от 2 до 3S. Расстояние между словами в предложении равно ширине образующейся при пропуске одной буквы или 2x(2-3)S+S. Расстояние между строк в многострочном тексте принимается чуть больше высоты букв (рис.6)
В графическом оформлении любого чертежа важное место занимает правильный выбор шрифта. Расчет надписей, выполненных узким архитектурным шрифтом, очень прост. Расстояние между буквами или пробел в узком архитектурном шрифте один и тот же. Слова одной высоты. Гарнитуры «узкого архитектурного шрифта» вписываются в узкие прямоугольники и площадь между буквами получаете практически одинаковой. Пропорции этого шрифт следующие: S норм = 1/6 Н, где S норм – ширина нормальной буквы, Н - высота буквы, S шир.=1,5S, где S шир. - ширина широких букв, их шесть: Ж, Ф, Ш, Щ, Ы, Ю. Необходимо также отметить, что цифры и буквы на чертеже, имеющие одинаковый размер, должны быть выполнены в одном стиле с хорошими сопряжениями. Радиус сопряжения равен 0,5S. Расстояние между буквами в слове равно от 2 до 3S. Расстояние между словами в предложении равно ширине образующейся при пропуске одной буквы или 2x(2-3)S+S. Расстояние между строк в многострочном тексте принимается чуть больше высоты букв (рис.6)
Рис. 6. Шрифт архитектурный узкий
Тема 1-3. Геометрические построения. Деление отрезков и углов. Способы построения многоугольников
Деление отрезка прямой на равные части может быть выполнено при помощи циркуля.

Рис.7. Деление отрезка на 2,4,..части. Рис.8. Деление отрезка на N частей.
Деление углов

Рис.9. Деление угла пополам.
Рис.10. Деление прямого угла на 3 части.
Способы построения многоугольников
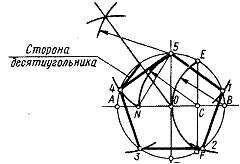

Рис.11. Построение правильных 3,4,5, 6 -ти и 10- угольников
Тема 1-4. Сопряжения. Архитектурные обломы
Плавный переход одной линии в другую посредством третьей линии называется сопряжением.


Рис.12. Построение касательной к окружности: а, б
а) через точку вне окружности б) через точку на окружности.


Рис.13 Построение общей касательной к двум окружностям:
а) внешнее касание б) внутреннее касание
Сопряжения углов

Рис.14. Сопряжение углов:
а) прямого,
б) острого,
в) тупого
г) прокатный профиль (уголок)

Рис.15. Сопряжение прямой и окружности дугой заданного радиуса
 Рис.16 Сопряжение двух окружностей
Рис.16 Сопряжение двух окружностей
а) внешнее б) внутреннее в) смешанное
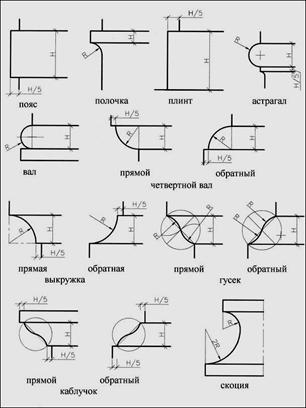 Архитектурные обломы
Архитектурные обломы
Исторические данные свидетельствуют о раннем появлении и постоянном присутствии архитектурных обломов на сооружениях. Профиля обломов представляют собой определенные типы поверхностей, которыми обрабатываются материалы постройки, эти поверхности протягиваются полосою на значительную длину. Сечение такой поверхности плоскостью дает кривую постоянного очертания по всей длине профиля. Очертания эти разнообразны и являются некоторой характеристикой стиля. При крайней простоте очертаний выступов они представляют собой пластическое выражение представлений, относящихся к разным механическим условиям и состояниям, в которых находятся отдельные части материала. Они как бы изображают те деформации, которые могут произойти под влиянием некоторых напряжений в некоторых местах.
Рис.17. Чертежи архитектурных обломов:
а) гусек, б) каблучек, в) четвертной вал, г) выкружка, д) скоция, е) вал, ж) полочка,
з) астрагал. I – прямые, II – обратные.
Раздел 2. Проецирование
Тема 2-1. Центральное и параллельное проецирование. Прямоугольное и косоугольное проецирование
Слово «проекция» латинское. В переводе на русский язык оно означает «бросать (отбрасывать) вперед».
Положите на бумагу какой-нибудь плоский предмет и обведите его карандашом. Вы получите изображение, соответствующее проекции этого предмета. Примерами проекций являются также фотографические снимки, кинокадры и др.
 Изображения предметов на чертежах в соответствии с правилами государственного стандарта выполняют по способу (методу) прямоугольного проецирования. Проецированием называют процесс построения проекции предмета.
Изображения предметов на чертежах в соответствии с правилами государственного стандарта выполняют по способу (методу) прямоугольного проецирования. Проецированием называют процесс построения проекции предмета.
Возьмем в пространстве произвольную точку А и какую-нибудь плоскость Н (рис.18). Проведем через точку А прямую так, чтобы она пересекала плоскость Н в некоторой точке а. Тогда точка а будет проекцией точки А. Плоскость, на которой получается проекция, называется плоскостью проекций. Прямую Аа называют проецирующим лучом. С его помощью точка А проецируется на плоскость Н. Указанным способом могут быть построены проекции всех точек любой пространственной фигуры.
Рис. 18. Получение проекций точки
Следовательно, чтобы построить проекцию какой-либо фигуры на плоскости, необходимо через точки этой фигуры провести воображаемые проецирующие лучи до их пересечения с плоскостью. Проекции всех точек фигуры образуют проекцию заданной фигуры. Рассмотрим получение проекции какой-нибудь геометрической фигуры, например треугольника (рис. 19).

Рис. 19. Проекция фигуры
Будем в дальнейшем обозначать точки, взятые на предмете, прописными буквами, а их проекции — строчными. Проекцией точки А на заданную плоскость и будет точка а как результат пересечения проецирующего луча Аа с плоскостью проекций. Проекциями точек В и С будут точки b и с. Соединив на плоскости точки а, b и с отрезками прямых, получим фигуру abc, которая и будет проекцией заданной фигуры ABC.
 Представление о проекции можно получить, рассматривая тени предметов. Возьмем, например, проволочную модель призмы (рис. 20). Пусть эта модель при освещении солнечными лучами отбрасывает тень на стену. Полученную таким образом тень можно принять за проекцию заданного предмета.
Представление о проекции можно получить, рассматривая тени предметов. Возьмем, например, проволочную модель призмы (рис. 20). Пусть эта модель при освещении солнечными лучами отбрасывает тень на стену. Полученную таким образом тень можно принять за проекцию заданного предмета.
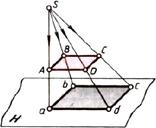
Рис. 20. Получение тени модели
Центральное и параллельное проецирование.
Если проецирующие лучи, с помощью которых строится проекция предмета, исходят из одной точки, проецирование называется центральным (рис. 21). Точка, из которой исходят лучи, называется центром проецирования. Полученная при этом проекция называется центральной.
Рис. 21. Центральное проецирование
Центральную проекцию часто называют перспективой. Примерами центральной проекции являются фотоснимки и кинокадры, а также тени, отброшенные от предмета лучами электрической лампочки и др. Центральные проекции применяют в рисовании с натуры.
Центральное проецирование представляет собой общий случай проецирования геометрических образов из некоторого центра на плоскость. Центральное проецирование обладает большой наглядностью и применяется в строительном черчении, в архитектуре, в живописи и т.п. Недостатком центрального проецирования является сложность построения изображения предмета и определения истинных размеров. Поэтому оно имеет ограниченное применение в техническом черчении
Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным, а полученная проекция - параллельной. Примером параллельной проекции можно условно считать солнечные тени предметов.
Строить изображение предмета в параллельной проекции проще, чем в центральной. В черчении такие проекции используются для построения чертежей и наглядных изображений.
При параллельном проецировании все лучи падают на плоскость проекций под одинаковым углом. Если это любой острый угол (рис.22), то проецирование называется косоугольным.


Рис. 22. Косоугольное проецирование Рис. 23. Прямоугольное проецирование
В том случае, когда проецирующие лучи перпендикулярны плоскости проекций (рис. 23), т. е. составляют с ней угол 90°, проецирование называют прямоугольным. Полученная при этом проекция называется прямоугольной.
Прямоугольное проецирование широко используется для построения изображений на чертежах.
Тема 2-2. Метод Монжа. Проецирование точек
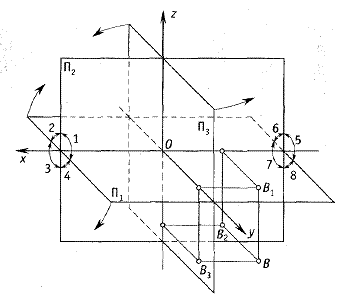 Выдающийся французский ученый – геометр Гаспар Монж (1746-1818) предложил метод прямоугольного проецирования на три взаимно перпендикулярные плоскости проекций: горизонтальную (Н), фронтальную (V) и профильную (W). Эти плоскости поделили предметное пространство на 8 частей, названных октантами.
Выдающийся французский ученый – геометр Гаспар Монж (1746-1818) предложил метод прямоугольного проецирования на три взаимно перпендикулярные плоскости проекций: горизонтальную (Н), фронтальную (V) и профильную (W). Эти плоскости поделили предметное пространство на 8 частей, названных октантами.
Ось X называется абсциссой;
Ось Y – ординатой;
Ось Z - аппликатой.
Рис.24.
Три взаимно перпендикулярные плоскости
Таблица 4. Знаки октантов
| октанты | I | II | III | IV | V | VI | VII | VIII |
| X | + | + | - | - | + | + | - | - |
| Y | + | - | - | + | + | - | - | + |
| Z | + | + | + | + | - | - | - | - |
Виды эпюров:
Трехосный эпюр – представлены все три оси координат X, Y и Z (рис.25). Одноосный эпюр – представлена только ось Х. Безосный эпюр – оси координат не представлены.

Горизонтальная проекция точки обозначается малой буквой без штриха – а, фронтальная – малой буквой с одним штрихом, профильная – малой буквой с двумя штрихами (рис.25).
Проекции точки соединяются между собой линиями связи, представляющими из себя замкнутый контур.
Если точка принадлежит одной из плоскостей проекций, то одна из проекций точки принадлежит оси координат.
Если точка принадлежит одной из осей координат, то две ее проекции совпадают.
Рис.25. Проецирование точек

Рис. 26. Прямоугольное проецирование:
а)фронтальная диметрия, б)эпюр
Тема 2-3. Проецирование прямых. Прямые общего и частного положения. Взаимное положение двух прямых
Прямая в пространстве определяется положением двух нетождественных точек. Условная запись определителя прямой l (А, В). Положение прямой в пространстве характеризуются углами наклона ее к плоскостям проекций π1, π2, π3. (а также р 1, р 2, р 3) или (П 1,П 2,П 3) или (П'П''П''') Следами прямой линии называются точки пересечения данной прямой линии с плоскостями проекций. Прямые линии общего положения имеют, как правило, два следа, прямые линии частного положения – один след.
 Прямая общего положения. Признак: ортогональные проекции прямой общего положения не параллельны и не перпендикулярны осям проекций.
Прямая общего положения. Признак: ортогональные проекции прямой общего положения не параллельны и не перпендикулярны осям проекций.
Прямые частного положения - прямые уровня. Это прямые параллельные плоскостям проекций. Признак: у прямых частного положения хотя бы одна ортогональная проекция параллельна или перпендикулярна оси проекций.
Рис. 27. Прямая общего положения
 а б в
а б в
Рис. 28. Прямые уровня: а) Горизонталь h. б) Фронталь f. в) Профильная прямая

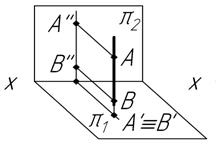 Рис. 29. Проецирующие прямые
Рис. 29. Проецирующие прямые
а) Горизонтально-проецирующая
б) Фронтально-проецирующая
а б
Взаимное положение двух прямых
Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.
1. Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек. Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если AB CD то A1B1 C1D1; A2B2 C2D2; A3B3 C3D3 (рис.30).
2. Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи (рис. 31).


Рис.30. Параллельные линии Рис.31. Пересекающиеся линии
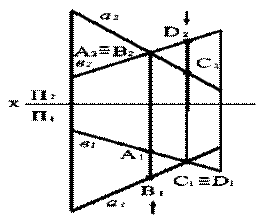 3. Скрещивающимися называются две прямые не лежащие в одной плоскости. Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи (рис.32).
3. Скрещивающимися называются две прямые не лежащие в одной плоскости. Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи (рис.32).
Рис. 32. Скрещивающиеся прямые
Тема 2-4. Проецирование плоскостей. Способы задания плоскости на эпюре. Плоскости общего и частного положения. Взаимное положение двух плоскостей. Пересечение плоскостей. Пересечение плоскости с прямой линией
При ортогональном проецировании любая плоскость может быть задана на чертеже проекциями следующим образом (табл. 5)
Таблица 5.Способы задания плоскости
| Способ задания | Наглядное изображение | Комплексный чертеж |
| а) тремя точками, не лежащими на одной прямой | 
| 
|
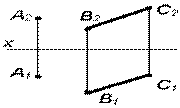
| б) прямой и точкой вне данной прямой |

| 
|
| в) двумя параллельными прямыми | 
| 
|
| г) плоской фигурой |

| 
|
| д) двумя пересекающимися прямыми | 
| 
|
| е) следом: Р ^ a |

|
Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций. Признак: ни одна из ортогональных проекций геометрических фигур, задающих плоскость общего положения, не сливается в прямую линию.
Таблица 6. Плоскость общего положения
| Определение | Наглядное изображение | Комплексный чертеж |
| Плоскость, не перпендикулярную ни к одной из плоскостей проекций, называют плоскостью общего положения | 
| 
|
Плоскость частного положения (плоскость уровня) параллельна или перпендикулярна хотя бы к одной из плоскостей проекций.
Таблица 7. Плоскости уровня
| Характеристика | Наглядное изображение | Эпюр | ||
Фронтальная плоскость – это плоскость, параллельная плоскости p2. Эта плоскость пересекает плоскость p1 параллельно оси ОХ, а плоскость p3 – по линии, параллельной оси OZ













 (D ABC)^ p1. Любой элемент, лежащий в этой плоскости, проецируется на плоскость p1 в прямую линию; горизонтальная проекция D A1B1C1 есть прямая линия на плоскости p1; угол b есть угол наклона этой плоскости к плоскостям p2. Он проецируется на горизонтальную плоскость без искажения
(D ABC)^ p1. Любой элемент, лежащий в этой плоскости, проецируется на плоскость p1 в прямую линию; горизонтальная проекция D A1B1C1 есть прямая линия на плоскости p1; угол b есть угол наклона этой плоскости к плоскостям p2. Он проецируется на горизонтальную плоскость без искажения
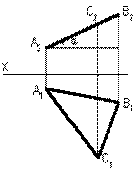











 Параллельные плоскости. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости
Параллельные плоскости. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости АС
АС

 D2
m1 || A1B1; m1
D2
m1 || A1B1; m1 


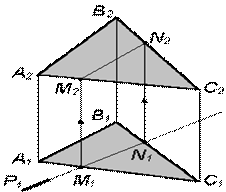

 2. Горизонтальные проекции линии пересечения данных плоскостей с вспомогательной плоскостью R (R2) дают первую общую точку М:
2. Горизонтальные проекции линии пересечения данных плоскостей с вспомогательной плоскостью R (R2) дают первую общую точку М:



 Для построения прямой, проходящей через заданную точку пространства, параллельно заданной плоскости, достаточно провести прямую, параллельную любой прямой, принадлежащей плоскости. При этом возможно множество решений
Для построения прямой, проходящей через заданную точку пространства, параллельно заданной плоскости, достаточно провести прямую, параллельную любой прямой, принадлежащей плоскости. При этом возможно множество решений

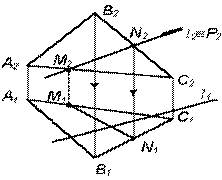


 Перпендикулярность прямой и плоскости. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (рис.42).
Перпендикулярность прямой и плоскости. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (рис.42).

 P1 (А1В1С1)
n2^f2; f2
P1 (А1В1С1)
n2^f2; f2 


 Рассмотрим, как изображают на чертеже правильную четырехугольную пирамиду (рис. 46). Основание пирамиды проецируется на горизонтальную плоскость проекций в натуральную величину. На нем диагоналями изображаются проекции боковых ребер, идущих от вершин основания к вершине пирамиды.
Рассмотрим, как изображают на чертеже правильную четырехугольную пирамиду (рис. 46). Основание пирамиды проецируется на горизонтальную плоскость проекций в натуральную величину. На нем диагоналями изображаются проекции боковых ребер, идущих от вершин основания к вершине пирамиды. проецируемого предмета и координатных осей.
На аксонометрической плоскости проекций получают изображение - аксонометрическую проекцию предмета, а также проекции осей систем координат, которые называют аксонометрическими осями.
Рис. 47. Получение аксонометрической (прямоугольной изометрической) проекции
Можно получить множество аксонометрических проекций, по-разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис. 50).
Наиболее употребляемой является так называемая прямоугольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название - изометрическая проекция). Изометрической проекцией (см. рис. 48, а) называется такая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью параллельного проецирования.
Рис.48. Аксонометрические проекции.
а- прямоугольная изометрическая;
б- прямоугольная диметрическая;
в
проецируемого предмета и координатных осей.
На аксонометрической плоскости проекций получают изображение - аксонометрическую проекцию предмета, а также проекции осей систем координат, которые называют аксонометрическими осями.
Рис. 47. Получение аксонометрической (прямоугольной изометрической) проекции
Можно получить множество аксонометрических проекций, по-разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис. 50).
Наиболее употребляемой является так называемая прямоугольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название - изометрическая проекция). Изометрической проекцией (см. рис. 48, а) называется такая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью параллельного проецирования.
Рис.48. Аксонометрические проекции.
а- прямоугольная изометрическая;
б- прямоугольная диметрическая;
в
