Геометрический смысл производной функции

 

Понятие касательной к кривой на плоскости

Рассмотрим некоторую кривую на плоскости, например график функции y = f (x),изображенной на рис.2. Проведем через некоторую фиксированную точку M и произвольную точку L на кривой прямую ML, называемую секущей. Прямая ML образует с положительным направлением оси 0x угол φ.

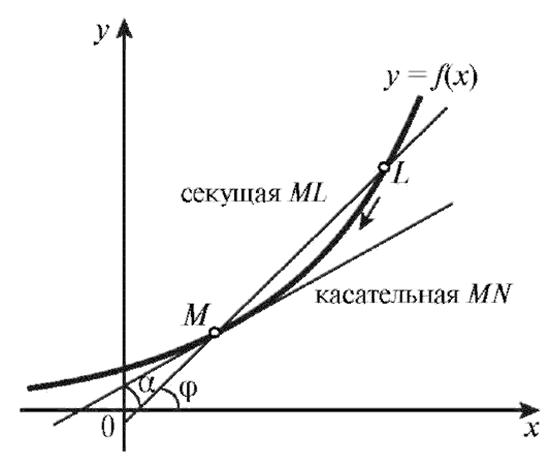
Рис.2.Касательная MN к кривой в точке M

 

Пусть точка L приближается к точке M по кривой. Тогда секущая ML стремится к некоторому предельному положению MN, образующему угол α с положительным направлением оси 0x. Если положение прямой MN не зависит от того, справа или слева от точки M находится точка L, то прямая MN называется касательной к кривой в точке M.

Геометрический смысл производной заключается в том, что производная функции
у = f (x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке:

 

 

Производные некоторых элементарных функций. Основные правила дифференцирования

Производные некоторых элементарных функций

 

Таблица производных основных элементарных функций

Основные правила дифференцирования

Для нахождения производных конкретных функций необходимо кроме таблицы производных использовать свойства производных, которые также называют основными правилами дифференцирования.

1. Постоянный множитель C можно выносить за знак производной:

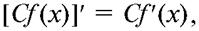
где C = const; f (x) - функция, дифференцируемая в точке x.

2. Производная суммы или разности (алгебраической суммы) двух (или нескольких) дифференцируемых в точке x функций равна сумме или разности производных этих функций:

[u(x) ± ν(x)]' = u(x) ± v'(x).

Здесь v(x) и u(x) - две функции.

3. Производная произведения двух дифференцируемых в точке x функций u(x) и v(x) рассчитывается по формуле:

 [u(x)∙v(x)]' = u(x)v'(x) + u'(x)∙ν(x).

4. Пусть u(x) и v(x) - две дифференцируемые в точке x функции,

причем v(x) ≠ 0. Тогда производная частного двух функций равна:

 

 

Определение дифференциала функции. Дифференциалом функции y = f (x) в точке x называется произведение производной функции в этой точке на приращение аргумента:

dy = f (x)∙Δx.

Здесь dy - обозначение дифференциала; f (x) - производная функции в точке x; Δx - приращение аргумента.

Как видно из определения, дифференциал функции в точке x зависит от приращения аргумента Δx. Величина Δx не зависит от x и может быть как положительной, так и отрицательной. Таким образом, чтобы вычислить дифференциал функции необходимо найти производную f' (х) и умножить на приращение Δx.

Пример. Найти дифференциал функции у = 3х⁴.

Решение: Найдем производную у' = 3∙4х^4-1 = 12х³. Тогда дифференциал dy будет равен: dy = 12х³ Δx.