Замечание №3.
Наиболее просто вычисляется момент, если сила располагается в плоскости перпендикулярной к оси.
Если сила находится в плоскости перпендикулярной оси, то ее момент относительно этой оси будет равен произведению этой силы на кротчайшее расстояние между этой осью и линией действия силы.
Изобразим силу  перпендикулярно оси Z. Кратчайшее расстояние от линии действия силы до оси Z есть плечо h.
перпендикулярно оси Z. Кратчайшее расстояние от линии действия силы до оси Z есть плечо h.
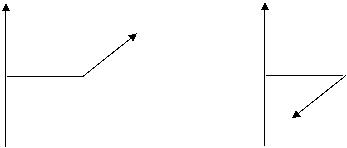 |
mZ( )=mZ(
)=mZ( )=
)= 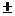 Fh
Fh
mZ( )=
)= 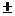 Fh
Fh
Зависимость между моментом силы относительно оси и любой точки лежащей на оси.
Момент силы относительно оси можно найти другим способом, не опираясь на принятое определение.
Изобразим ось Z и произвольную силу  . На оси возьмем произвольную точку О. Построим векторный момент этой силы относительно точки О.
. На оси возьмем произвольную точку О. Построим векторный момент этой силы относительно точки О.
 Z
Z  .
.
B
mOZ ( )
)
γ  A
A
в
O
a
Этот момент будет перпендикулярен плоскости треугольника ОАВ.
Оказывается, что момент этой силы  относительно оси Z равен проекции векторного момента на ось Z
относительно оси Z равен проекции векторного момента на ось Z
mZ ( )= mOZ (
)= mOZ ( )
)
mOZ ( ) – проекция векторного момента mZ (
) – проекция векторного момента mZ ( ) на ось Z
) на ось Z
Для того чтобы этим способом найти момент силы относительно оси сначала найдем векторный момент относительно точки, а затем спроектируем векторный момент на ось. А до этого мы должны были спроектировать силу на плоскость, а затем находить момент проекции этой силы относительно точки.
Доказательство:
По модулю момент силы  относительно точки О равен
относительно точки О равен
׀  (
( )׀= 2 пл.
)׀= 2 пл.  ОАВ
ОАВ
а момент относительно оси Z этой силы  равен
равен
mZ ( )=2 пл.
)=2 пл.  Оав
Оав
Нижний треугольник сточки зрения геометрии это проекции верхнего треугольника на плоскость. А она равняется площадь верхнего треугольника на косинус угла между треугольниками.
Запишем:
пл.  Оав = пл.
Оав = пл.  ОАВ cos γ,
ОАВ cos γ,
где γ - угол между плоскостями треугольников, равный углу между нормалями к ним, то есть углу между mO ( ) и Z.
) и Z.
Следовательно
mZ ( )=2 пл.
)=2 пл.  ОАВ cos γ
ОАВ cos γ
Или
mZ( )= ׀
)= ׀ 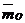 (
( ) ׀ cos γ
) ׀ cos γ
теперь смотрим по рисунку, из которого видно:
mO ( )cos γ = moZ(
)cos γ = moZ( )
)
Поэтому окончательно получим
mZ ( )= moZ (
)= moZ ( ) (7)
) (7)
Последняя формула выражает следующую теорему:
Момент данной силы относительно оси равен проекции на эту ось векторного момента этой в силы относительно любой точки лежащей на этой оси.
5 Аналитическое выражение момента силы относительно координатных осей.
(Теорема Вариньона)
Изображаем произвольную систему координат OXYZ и три составляющие силы  (
(

 ) Координаты точки А следующие XYZ
) Координаты точки А следующие XYZ
 Z
Z 

A 

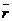
O Y
X
Y
X
Представим силу  , как равнодействующую сил
, как равнодействующую сил 

 ;
;
 =
=  +
+  +
+ 
Затем умножим это векторное равенство слева на вектор 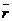 ,
,
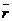
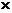
 =
= 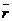
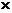
 +
+ 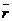
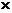
 +
+ 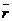
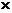

Получаем
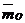 (
( )=
)= 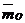 (
( )+
)+ 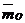 (
( )+
)+ 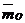 (
( ) (8)
) (8)
Спроецируем это равенство на координатные оси и воспользуемся теоремой из пункта 4
moX( ) =mX(
) =mX( )
)
moY( ) =mY(
) =mY( )
)
moZ ( ) = mZ (
) = mZ ( )
)
 окончательно
окончательно
mX ( ) = mX (
) = mX ( ) + mX (
) + mX ( ) + mX (
) + mX ( )
)
mY( ) = mY(
) = mY( ) + mY(
) + mY( ) + mY(
) + mY( ) (9)
) (9)
mZ( ) = mZ(
) = mZ( ) + mZ(
) + mZ( ) + mZ(
) + mZ( )
)
Формулы 8 и 9 выражают теорему Вариньона 1654-1722 выдающийся французский ученый, математик механик.
Формулировка.




