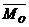 =
= 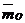 (
(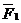 )+
)+ 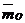 (
(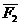 ) (4)
) (4)
Причем точка О произвольная точка.
Преобразуем формулу (4). Введем радиус вектор точки А относительно точки О и радиус вектор очки В относительно точки О.
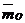 (
(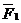 )=
)= 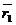
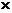
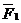 ,
, 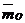 (
(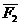 )=
)= 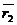
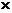
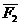
Тогда можно записать:
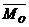 =
= 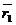
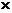
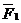 +
+ 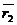
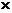
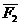
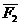 = -
= - 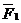
Тогда
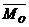 =(
=(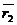 -
- 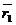 )
) 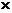
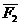
из рисунка видно, что
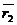 -
- 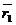 =
= 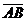
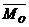 =
= 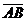
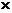
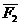 =
= 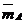 (
(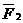 ) (5)
) (5)
где 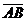 это радиус вектор точки приложения силы
это радиус вектор точки приложения силы 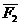 относительно точки А, момент силы
относительно точки А, момент силы 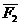 относительно точки А.
относительно точки А.
Преобразуем эту формулу с помощью 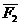 = -
= - 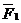
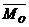 =
= 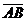
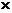 (-
(- 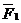 )=
)= 
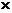
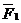 =
= 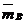 (
(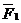 ) (6)
) (6)
где  это радиус вектор точки приложения силы
это радиус вектор точки приложения силы 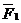 относительно точки В.
относительно точки В.
Вектор 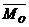 - не зависит от выбора точки О. Следовательно, вектор
- не зависит от выбора точки О. Следовательно, вектор 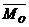 - вектор свободный. Его можно прикладывать в любой точке тела: А, В, и т.д.
- вектор свободный. Его можно прикладывать в любой точке тела: А, В, и т.д.
Например, приложим его в точке О.
По определению векторного произведения 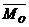 перпендикулярен плоскости действия пары. Этот вектор направлен в ту сторону, откуда поворот тела пары виден против часовой стрелки.
перпендикулярен плоскости действия пары. Этот вектор направлен в ту сторону, откуда поворот тела пары виден против часовой стрелки.
Определим модуль этого вектора:
МО= АВ  F 2
F 2 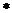 sin (
sin ( 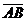 ,
, 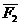 )= F 2
)= F 2 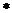 d
d
МО=АВ  F 2 =ВА
F 2 =ВА  F 1
F 1
Вывод:
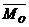 полностью учитывает все три фактора, от которых зависит вращательное действие пары.
полностью учитывает все три фактора, от которых зависит вращательное действие пары.
Поэтому этот вектор примем в качестве векторного момента пары.
 =
= 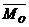 ,
,
таким образом
 =
= 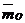 (
(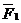 )+
)+ 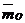 (
(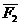 )
)
 =
= 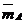 (
(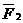 ) (7)
) (7)
 =
= 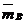 (
(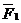 )
)
Определение.
Векторным моментом пары называется векторная величина равная сумме векторных моментов сил пары относительно произвольной точки или векторному моменту одной из ее сил пары относительно точки приложения другой силы.
Будем момент пары прикладывать так, как указано на рисунке, в середине плеча
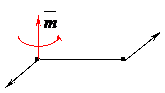 | |||||
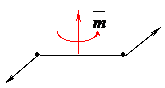 | 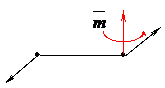 | ||||
Т.к. момент пары полностью характеризует вращательный эффект действия пары, то не обязательно указывать саму пару, достаточно указать только ее момент.
Алгебраический момент пары.
Рассмотрим некоторую плоскую систему пар.
У всех пар этой системы общая плоскость поворота.
В этом случае векторные моменты пар будут колинеарными (параллельными) друг к другу, поэтому в этом случае целесообразно момент рассматривать как величину скалярную, а точнее как алгебраическую. Направление поворота пары будем определять знаком. Знак «плюс» будет показывать, что тело вращается под действием пары против часовой стрелки, а знак «минус» поворот по часовой стрелки.
В этом случае целесообразно под моментом любой пары понимать величину алгебраическую.
МО= mO (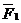 )+ mO (
)+ mO (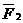 ),
),
или
МО= 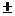 F 1 d =
F 1 d = 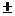 F 2 d
F 2 d
Алгебраическим моментом пары называется алгебраическая величина равная сумме алгебраических моментов сил пары относительно произвольной точки, или со знаком плюс или минус модуля одной из сил пары на плечо пары.
Правило знаков:
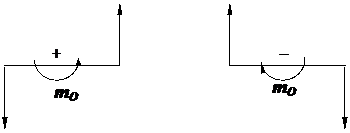 |
Момент считается положительным, если пара стремится повернуть тело против хода часовой стрелки, и отрицательным, если по ходу часовой стрелки.
Операции над парами
Пары будут эквивалентными друг другу, если они оказывают одинаковое вращательное действие на данное тело. Пары будут эквивалентными, если они имеют одинаковые моменты (векторные или алгебраические).
Над парами можно производить такие операции, которые не изменяют их моменты.
Операция №1.
Изобразим пару и плоскость ее действия.






