Мы ввели понятие меры вращательного действия силы вокруг некоторой точки. Если речь идет о силах, которые образуют пространственную систему сил, то тогда под моментом будем понимать величину векторную. Если же будем рассматривать силы лежащие в одной плоскости, то в этом случае будем пользоваться моментом силы алгебраическим.
3. Момент силы относительно оси.
Изображаем три картинки
 |
1. 2. 3.
На первой картинке сила параллельна оси. На второй сила пресекает ось. На третьей картинке сила перпендикулярна оси.
На первой картинке сила может только смещать тело вдоль оси. Такая сила не обладает вращательным эффектом.
На второй картинке сила тоже не может повернуть тело.
А вот на третей картинке сила перпендикулярна, обладает вращательным эффектом. Она не может смещать тело вдоль оси Z, но повернуть, стремиться.
Рассмотрим общий случай, когда сила располагается как угодно в пространстве.
Сила приложенна в точке А и располагается совершенно проимвольно по отношению к оси Z.
Совершим следующее построение.
Через точку А, точку приложения силы проводим плоскость перпендикулярную оси Z.
Эту плоскость мы обозначим через XY. А точку приложения этой плоскости с осью обозначим через О.Силу 
разложим на две составляющие, по правилу параллелограмма. Одна составляющая будет перпендикулярна этой плоскости и параллельна оси Z, а другая лежит в этой плоскости.
Обозначим составляющую, принадлежащую этой плоскости через 
, а составляющую параллельную оси ОZ - 
. Начало и конец вектора обозначим маленькими буквами "а" и "в".
Z
В
O
XY
Для чего мы сделали такое построение?
Мы должны ввести понятие момента силы относительно оси Z, а пока разложили силу на составляющие.
Составляющая не обладает вращательным эффектом.
Вращательный эффект данной силы относительно оси Z полностью заключен в составляющей , поэтому момент силы относительно оси Z будем определять
mZ ()= mZ (),
а величину mZ() определяем формулой mZ() это момент силы относительно точки О, который равен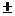 
F XYh
Окончательно приходим к следующей формуле:.
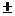mZ(,) = mO ()= F XYh
Итак,
mZ(,) = 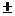F XYh (5)
Определение.
Моментом силы относительно оси называется алгебраическая величина равная моменту проекции этой силы на любую плоскость перпендикулярную оси, относительно точки О пересечения оси с плоскостью.
Момент силы считается положительным, если смотря с положительного конца оси Z, поворот который стремится совершить сила виден происходящим против часовой стрелки, впротивном случае он будет отрицательным.
Показать на примере ручки.
Замечание №1
Этот момент будет равен
| mZ ()|=2 пл. 
Оав (6)
Замечание №2
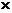mZ ()=0, || OZ
OZ
