В этом случае сила пытается сообщить телу поступательное движение.
На второй картинке изобразим цилиндрический шарнир и обозначим его через 0, и прикладываем к нему некоторую силу 
.
 |
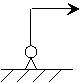В этом случае сила стремится повернуть тело вокруг центра шарнира (точки 0) т.е. сообщить вращательное движение.
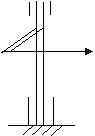
На третьей картинке изобразим ось закрепленную вверху подшипником, а внизу поставим подпятник. И тоже приложим силу.
Сила стремится повернуть тело вокруг оси Z, т.е. сообщить вращательное движение вокруг оси.
 |
На всех рисунках изображена одна и та же сила.
На первой картинке действие силы на тело полностью характеризуется вектором силы.
А вот на второй и третей вектор силы не вполне определяет действие силы на тело. Потому, что действие этой силы будет зависеть не только от вектора этой силы, но и от того, как он будет располагаться относительно точек 0 и оси Z.
Получается, что вектор силы не всегда полностью определяет действие силы на тело.
Поэтому необходимо ввести дополнительную характеристику, которая будет учитывать вращательный эффект вызываемой силы. Этой мерой вращательного действия будет являться момент силы.
Вектор силы не всегда полностью характеризует действие силы на тело.
Мерой вращательного действия силы на тело является величина, которая называется моментом силы.
Различают два вида моментов
Момент силы относительно точки или центра.
Момент силы относительно оси.
2. Момент силы относительно точки или центра.
2.1 Векторный момент.
Пусть S некоторая пространственная система сил.
Предположим, что силы этой системы стремятся повернуть тело вокруг точки 0.
Рассмотрим силу, приложенную в точке А.
 |
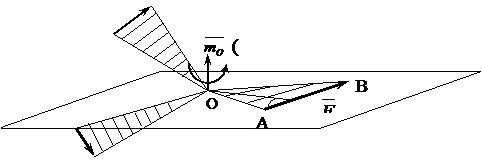Плоскость АОВ называется плоскостью поворота силы .
Из точки О на линию действия силы опускаем перпендикуляр, который является плечом силы относительно 0.
Точка 0 называется центром момента
Теперь мы должны внести математическую величину, которая действительно будет учитывать вращательное действие силы на тело.
Мы бы будем определять эту величину, опираясь на наблюдение.
Наблюдение показывает, что вращательное действие силы зависит от трех факторов:
1) модуля силы и плеча h (от комплекса (произведения) на h)
Fh - численная характеристика интенсивности вращательного действия силы.
Важно именно это произведение, потому что можно добиться большого эффекта малой силой, но взяв большое плечо и наоборот,большой силой, но малым плечом
Существенно именно произведение Fh.
От ориентации в пространстве плоскости поворота(показать макет)
от направления поворота в этой плоскости.
В математике показывают ориентацию плоскости в пространстве с помощью орта нормали.
Потому, если договоримся под моментом относительно точки понимать вектор и направлять по нормали к плоскости поворота, тем самым мы уже будем знать, как ориентируется плоскость поворота.
Мы будем прикладывать этот вектор в центре 0. От нас зависит в какую сторону.
Мы работаем в правой системе координат, следовательно, будем направлять в ту сторону, откуда поворот будет виден нам против часовой стрелки.
Момент силы относительно точки 0 будем рассматривать как вектор, направленный по нормали к плоскости поворота, и прикладывать в центре момента 0.
Будем направлять в ту сторону, откуда поворот, который сила стремиться сообщить телу, виден против часовой стрелки, а модуль этого вектора будем считать равным произведению силы на плечо.
Убедимся, что всем трем факторам можно удовлетворить, если векторный момент определять следующим образом:
()= 
= 
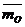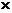
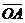
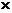
(1)
где радиус вектор точки А приложения силы, относительно точки О или .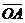
Выясним, как направлен этот момент.
По определению векторного произведения вектор 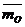() направлен перпендикулярно площадке содержащей (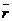
, ), т.е. перпендикулярен плоскости поворота.
Вектор направлен так, как указано на рисунке. ()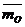
Осталось выяснить определяет ли это выражение правильно модуль.
Вычислим модуль:
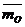׀ ()׀=׀ ׀׀ ׀ sin (, )= F r sin (r, F) = Fh (2)
Действительно формула (1) учитывает все три фактора, от которых зависит вращательное действие силы. Формула (1) есть не что иное, как символическое определение векторного момента. Эту запись мы переведем на обычный язык.
Определение:
Векторным моментом любой силы пространственной системы, относительно некоторой точки (центра) называется величина равная векторному произведению радиуса-вектора точки приложения силы относительно центра момента, на вектор силы.
Замечание №1
С точки зрения геометрии Fh это удвоенная площадь ОАВ.
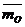׀ ()׀= 2 пл. 
ОАВ
Замечание№2
