Уравнением Лагранжа называется дифференциальное уравнение первого порядка, линейное относительно  и
и 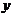 , коэффициентами которого служат функции от
, коэффициентами которого служат функции от 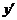 :
:
P(y')x + Q(y')y + R(y') = 0
Уравнение Лагранжа интегрируем следующим образом. Разрешим его относительно 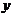 и примем за параметр y ' полагая y ' = p:
и примем за параметр y ' полагая y ' = p:
y = xf (p) + φ (p).
Здесь введены обозначения:
f (y') = – P (y')/ Q (y'), φ (y')= – R (y')/ Q (y').
Дифференцируя полученное уравнение и заменяя в левой части 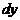 на
на 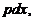 приходим
приходим
к уравнению
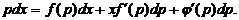
Полученное уравнение — линейное относительно  (как функции от
(как функции от  ) и поэтому может быть проинтегрировано.
) и поэтому может быть проинтегрировано.
Если его решение есть 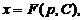 то общее решение исходного уравнения Лагранжа запишется в виде
то общее решение исходного уравнения Лагранжа запишется в виде
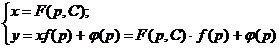 .
.
Уравнением Клеро называется уравнение первой степени (т.е. линейное) относительно функции и аргумента вида
 ,
,
которое является частным случаем уравнения Лагранжа. С учетом замены 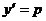 , уравнение принимает вид
, уравнение принимает вид 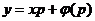 .
.

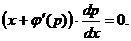
Последнее уравнение имеет два возможных решения:  или
или 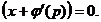
В первом случае 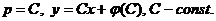 Видно, что общее решение представляет собой семейство прямых линий.
Видно, что общее решение представляет собой семейство прямых линий.
Во втором случае 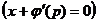 решение в параметрической форме выражается системой уравнений:
решение в параметрической форме выражается системой уравнений: 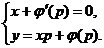 Исключив параметр
Исключив параметр 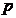 , получаем второе уравнение
, получаем второе уравнение 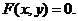 Это решение не содержит произвольной постоянной и не получено из общего решения, следовательно, не является частным решением. Это решение будет являться особым интегралом.
Это решение не содержит произвольной постоянной и не получено из общего решения, следовательно, не является частным решением. Это решение будет являться особым интегралом.
Иными словами, общим решением уравнения Клеро служит семейство касательных к особому решению.
Уравнение Лагранжа также может иметь особые решения, причем особыми решениями этого уравнения (если они существуют) являются общие касательные ко всем интегральным кривым, определяемым общим решением.
Пример 1. Проинтегрировать уравнение 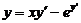 .
.
Решение. Это уравнение Клеро. Пусть  , тогда
, тогда 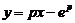 . Продифференцируем его:
. Продифференцируем его: 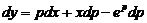 ;но
;но 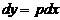 , поэтому
, поэтому 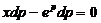 , или
, или 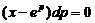 .
.
Таким образом, либо 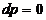 , либо
, либо  . Если положить
. Если положить 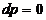 , то
, то  . Подставляя это значение р в равенство
. Подставляя это значение р в равенство 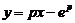 , получаем общее решение данного уравнения:
, получаем общее решение данного уравнения: 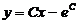 .
.
Если положить  , то
, то 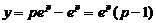 . Получим особое решение данного уравнения:
. Получим особое решение данного уравнения:
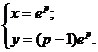
Или, исключая параметр p (p = ln x), находим особое решение в явном виде:  .
.
Пример 2. Решить уравнение  .
.
Решение. Это уравнение Лагранжа. Положим y ' = p, тогда y = xp 2 + p 2 = p 2(x + 1). Продифференцируем последнее равенство:
dy = p 2 dx + 2 pxd р + 2 pdp.
Заменяя 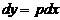 , получим уравнение
, получим уравнение
 .
.
Сокращая на p, получаем уравнение с разделяющимися переменными:
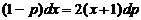 ,
,
или
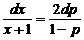 .
.
Интегрируя, получим 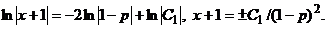
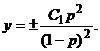
Сокращение на p могло привести к потере особого решения. Полагая p = 0, находим y = С. Это особое решение.
Итак,
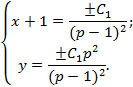
- общее решение;
y = С – особое решение.
В общем решении параметр p можно исключить и тогда оноприводится к виду





