Линейные однородные уравнения высших порядков с постоянными коэффициентами

Лекция 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

Линейным дифференциальным уравнением n -го порядка называется уравнение вида

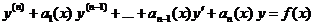,(7)

где функции а ₁(х), а ₂(х),..., а _n (х), f (x) заданы и непрерывны в некотором промежутке (а, b).

Если в уравнении (7) f (x) ¹ 0, то оно называется линейным неоднородным, или уравнением с правой частью.

Если в уравнении (7) f (x) = 0, то оно принимает вид

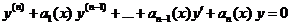(8)

и называется линейным однородным, или уравнением без правой части.

Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему.

Одним из замечательных свойств линейных уравнений является то, что общее решение таких уравнений можно найти по их известным частным решениям.

Общее решение линейного однородного уравнения находят исходя из следующей теоремы.

Теорема. Если у ₁, у ₂,..., у _n — линейно независимые частные решения уравнения (8), то

у = С ₁ у ₁ + С ₂ у ₂ +... + С _n у _n,                                      (9)

где С ₁, С ₂ ,..., С _n — произвольные постоянные, является общим решением уравнения (8).

Решение задачи Коши для уравнения (8) находят следующим образом:

1) находят постоянные С ₁, С ₂ ,..., С _n по заданным начальным условиям;

2) подставляют найденные значения С₁, С₂,..., С _n в формулу (9) общего решения.

Напомним, что функции у ₁(х), у ₂(х),..., у _n (х)называются линейно зависимыми в промежутке (а, b), если существуют такие постоянные a₁, a₂,..., a _n, не равные нулю одновременно, что

a₁ у ₁ + a₂ у ₂ +... + a _n у _n = 0.

В противном случае данные функции называются линейно независимыми.

Для случая двух функций условие линейной зависимости принимает вид   

a₁ у ₁ + a₂ у ₂ = 0, или ,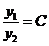

где С — постоянная величина.

 

Примеры. 1) у ₁ = 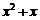, у ₂ = 3 х (х + 1) — линейно зависимые функции; 2) у ₁ = 2 ,
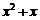у ₂ = 2 ‑ 1 — линейно независимые функции; 3) у ₁ = 3 cos 2 x, у ₂ = 4 cos 2 х — линейно зависимые функции; 4) у ₁ = 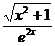, у ₂ =  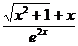— линейно независимые функции.

Совокупность линейно независимых частных решений уравнения (8) у ₁, у ₂,..., у _n называется фундаментальной системой решений.

Для того, чтобы система частных решений уравнения (8) у ₁, у ₂,..., у _n былафундаментальной, т.е. линейно независимой в промежутке (а, b), необходимо и достаточно, чтобы " х Î (а, b) определитель Вронского (вронскиан) не был равен нулю:

.

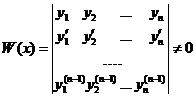Общее решение линейного неоднородного уравнения (7) имеет вид

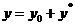,                                                  (10)

где у ₀– общее решение соответствующего линейного однородного уравнения (8);

у * – частное решение данного линейного неоднородного уравнения (7).

Если известна фундаментальная система решений у ₁, у ₂,..., у _n однородного уравнения (8), то общее решение соответствующего неоднородного уравнения (7) можно найти также методом вариации произвольных постоянных, который рассмотрим в п. 2.5.

Линейные однородные уравнения высших порядков с постоянными коэффициентами

Линейным однородным уравнением спостоянными коэффициентами называется уравнение вида

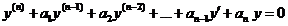,                       (11)

где  а ₁, а ₂,..., а _n — некоторые действительные числа.

Это частный случай уравнения (8), когда выполняется условие:

а _i (х) = а _i =const (i = 1, 2,..., n).

Для нахождения частных решений уравнения (11) составляют характеристическое уравнение

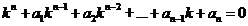,                              (12)

которое получается из уравнения (11) заменой в нём производных искомой функции у соответствующими степенями k, а саму функцию у заменяют единицей. Так как уравнение (12) является уравнением n -й степени относительно неизвестного k, то оно имеет n корней действительных или комплексных, среди которых могут быть и равные.

Общее решение уравнения (11) имеет вид (9) и строится в зависимости от характера корней уравнения (12) по следующему правилу:

1) каждому действительному простому корню k в общем решении (9) соответствует слагаемое вида С × е ^kx;

1) каждому действительному корню кратности m в общем решении (9) соответствует слагаемое вида (С ₁ + C ₂ x + C ₃ x ² +... + C_mx^{m - 1}) × е ^kx;

3) каждой паре комплексных сопряжённых простых корней k _1,2 = б ± в i в общем решении (9) соответствует слагаемое вида е ^{a x} × (С ₁cosb x + C ₂sinb x);

4) каждой паре комплексных сопряжённых корней k _1,2 = a ± b i кратности m в общем решении (9) соответствует слагаемое вида

е ^{a x} ((С ₁ + C ₂ x +... + C_mx^{m – 1})cosb x + (С ₁ + C ₂ x +... + C _m x^{m – 1})sinb x).

Пример 1. Найти общее решение уравнения .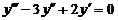

Решение. Данное уравнение является линейным однородным уравнением третьего порядка спостоянными коэффициентами. Запишем для него характеристическое уравнение

.

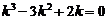Его корни k ₁ = 0, k ₂ = 1, k ₃ = 2 — простые действительные числа (случай 1). Следовательно, е ^{0× x} = 1, е ^{1× x} = е ^x, х · е ^x — частные линейно независимые решения, а общее решение данного уравнения имеет вид

у = С ₁ + C ₂ е ^x + C ₃ е^2х.

 

Пример 2. Найти общее решение уравнения .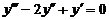

Решение. Данное уравнение является линейным однородным уравнением третьего порядка спостоянными коэффициентами. Запишем для него характеристическое уравнение

.

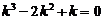Его корни: k ₁= 0 — простой действительный корень (случай 1), k _2,3 = 1 — действительный корень кратности 2 (случай 2). Следовательно, е ^{0× x} = 1, е ^{1× x} = е ^x, x × е ^x — частные линейно независимые решения, а общее решение данного уравнения имеет вид

у = С ₁ + C ₂ е ^x + C ₃ хе^2х.

 

Пример 3. Найти общее решение уравнения .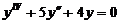

Решение. Данное уравнение является линейным однородным уравнением четвёртого порядка спостоянными коэффициентами. Запишем для него характеристическое уравнение

.

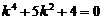Его корни: k _1,2 = ± i, k _3,4 = ± 2 i — две пары комплексных сопряжённых простых корней (случай 3; a = 0, b = 1 для первой пары корней и b = 2 для второй пары корней). Следовательно, е ^{0× x} × cos x = cos x, е ^{0× x} × sin x = sin x, е ^{0× x} × cos 2 x = cos 2 x, е ^{0× x} × sin 2 x = sin 2 x — частные линейно независимые решения, а общее решение данного уравнения имеет вид

у = С ₁ cos x + C ₂sin x + С₃ cos 2 x + C ₄sin 2 x.

 

Пример 4. Найти общее решение уравнения .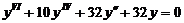

Решение. Данное уравнение является линейным однородным уравнением шестого порядка спостоянными коэффициентами. Запишем для него характеристическое уравнение

.

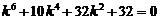Для нахождения корней преобразуем характеристическое уравнение к виду 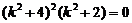. Откуда имеем: k _1,2 = ± 2 i — комплексные сопряжённые корни кратности 2 (случай 4; a = 0, b = 2); k _3,4= ± 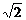i — пара комплексных сопряжённых простых корней (случай 3; a = 0, b = 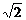). Следовательно, общее решение данного уравнения имеет вид

у = (С ₁+ C ₂ x)cos 2 x + (С₃ + C ₄ x)sin 2 x + С₅cos 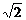x + C ₆sin 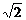x.

Выделим особо частный случай линейных однородных уравнений n - го порядка спостоянными коэффициентами (11) при n = 2, т.к. решение различных практических задач часто сводится к решению уравнений именно второго порядка.

Линейным однородным уравнением второго порядка спостоянными коэффициентами называется уравнение вида

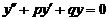,                                             (13)

где p, q — некоторые действительные числа.

Для практического использования указанный алгоритм оформим в виде таблицы 1.

 

На основании теории, рассмотренной в п. 2.3, получим следующий алгоритм решения линейных однородных уравнений второго порядка с постоянными коэффициентами.

1. Записать дифференциальное уравнение в виде (13).

2. Составить его характеристическое уравнение

.

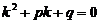3. Вычислить дискриминант D = p ²– 4 q.

а) Если D > 0, то уравнение имеет два разных действительных корня k ₁, k ₂, а общее решение записывается в виде

у = С ₁ × 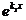+ C ₂ × .

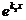б) Если D = 0, то уравнение имеет два одинаковых корня k ₁ = k ₂= k, а общее решение записывается в виде

у = С ₁ × е ^kx + C ₂ × х × е ^kx.

в) Если D < 0, то уравнение имеет пару комплексных сопряжённых корней k _1,2 = a±b i, а общее решение записывается в виде

е ^{a x} × (С ₁cosb x + C ₂sinb x).

Для практического использования указанный алгоритм представим в табл. 1.

 

Таблица 1. Решение линейного однородного уравнения
2-го порядка с постоянными коэффициентами

Дифференциальное уравнение
Характеристическое уравнение
Дискриминант	D > 0	D = 0	D < 0
Корни характеристичес­кого уравнения	k 1¹ k 2Î R	k 1= k 2= k Î R	k 1,2 = a ± b i Î C
Общее решение	С 1 + C 2	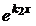С 1 е kx + C 2 х е kx	е a x (С 1cos b x + C 2sin b x)

 

Пример 5. Найти общее решение уравнения .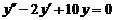

Решение. Данное уравнение является линейным однородным уравнением второго порядка спостоянными коэффициентами. Запишем для него характеристическое уравнение

.

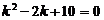Его корни (D < 0) k _1,2 = 1 ± 3 i — комплексные сопряжённые числа (случай 3; a = 1, b = 3), следовательно, е ^x cos 3 x, е ^x sin 3 x — частные линейно независимые решения, а общее решение данного уравнения имеет вид

у = е ^x (С ₁cos 3 x + C ₂sin 3 x).

 

Пример 6. Найти частное решение уравнения 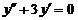,удовлетворяющее начальным условиям: у (0) = 1, .

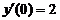Решение. Данное уравнение является линейным однородным уравнением второго порядка спостоянными коэффициентами. Запишем для него характеристическое уравнение

.

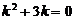Его корни (D > 0) k ₁= 0, k ₂= – 3 — простые действительные числа (случай 1). Следовательно, общее решение данного уравнения имеет вид

у = С ₁+ C ₂ е^–3х.

Дифференцируем это решение: у' = – 3 C ₂ е^-3х. Подставляя начальные условия в общее решение и его производную, получим систему уравнений относительно С ₁и C ₂:

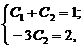
откуда С ₁= 5/3, C ₂ = – 2/3. Значит решение, удовлетворяющее заданным начальным условиям, имеет вид

.

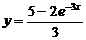Пример 7. Распространение тепла в стержне.

Длинный тонкий стержень, сделанный из металла с теплопроводностью l, находится в состоянии теплового равновесия, т.е. температура точек стержня не изменяется во времени. Потеря тепла через поверхность стержня в окружающую среду, температура которой w ₀ = const, пропорциональна разности температур с постоянным коэффициентом теплопередачи a. Считая температуру w во всех точках поперечного сечения стержня постоянной, найти её зависимость w = w (х) от координаты, отсчитываемой от какого-либо, например левого, конца (рис. 11).

Решение. Пусть длина стержня равна l, периметр поперечного сечения Р, площадь поперечного сечения Q. Выделим элемент стержня длиной dx, находящийся на расстоянии х от левого конца (рис. 11).

 

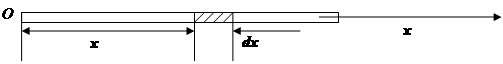
Рис. 11

 

Примем его температуру равной w. За время D t через левую границу этого элемента пройдёт количество тепла , а через правую на расстоянии х + D х от конца .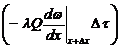

Таким образом, выделенный участок приобретает за время D t количество тепла, равное разности

‑  =  = »
» .

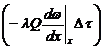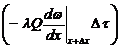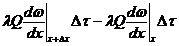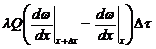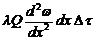Потеря тепла этого элемента через поверхность в окружающую среду равна 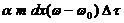, и если процесс стационарный, то эта величина равна найденной нами:

 = .

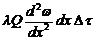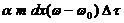
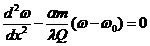Так как w ₀ = const, положив w – w ₀ = u, получим

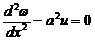,где .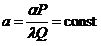

Таким образом, получили линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение имеет вид

u = С ₁ е ^{a х} + C ₂ е^{- a х} , или

w = w₀ + С ₁ е ^{a х} + C ₂ е^{- a х},

где С ₁ и С ₂ находят по дополнительным (краевым) условиям.

Пусть, например, на обоих концах стержня поддерживается постоянная температура w ₁ и w ₂(w ₂ < w ₁). Тогда краевые условия имеют вид: w (0) = w ₁; w (l) = w ₂. Подставляя их в общее решение, находим

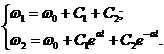
Решая полученную систему, находим С ₁ и С ₂, а затем соответствующее частное решение, удовлетворяющее заданным краевым условиям.