Лекция 2 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-ГО ПОРЯДКА
(продолжение)
Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид
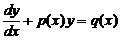 , (17)
, (17)
где p (x) и q (x) — заданные непрерывные функции.
Если q (x) = 0, то уравнение (17) называется линейным однородным. Оно является уравнением с разделяющимися переменными и решается, как указано в п. 1.1.
Если q (x) ≠ 0, то уравнение (17) называется линейным неоднородным. Для нахождения его решения используют метод Лагранжа (метод вариации произвольной постоянной) или метод Бернулли (метод подстановки).
Метод Лагранжа
Метод Лагранжа предполагает, что сначала находят общее решение линейного однородного уравнения
 , (18)
, (18)
соответствующего данному неоднородному уравнению (17). Так как оно является уравнением с разделяющимися переменными, то разделив переменные и проинтегрировав, получают
 ,
,
 .
.
Потенцируя, находят общее решение уравнения (18):
 , (19)
, (19)
где С — произвольная постоянная.
Далее находят общее решение линейного неоднородного уравнения (17) в виде (19), где С считают не постоянной, а новой неизвестной функцией от х, т.е. в виде
 . (20)
. (20)
Для нахождения функции С (х) подставляют (20) в исходное уравнение (17):
 ,
,
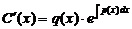 .
.
Интегрируют, получают:
 ,
,
где С 1 — произвольная постоянная.
Подставляя найденное выражение для С (х) в (19), получают общее решение линейного неоднородного уравнения:
 .
.
Пример 1. Найти общее решение уравнения
 .
.
Решение. Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка, где р (х) = 2 х, q (x) = 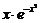 . Решим его методом вариации произвольной постоянной.
. Решим его методом вариации произвольной постоянной.
1) Сначала решим соответствующее однородное уравнение
y ' + 2 xy = 0.
Разделяя переменные 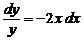 и интегрируя, находим
и интегрируя, находим
 ,
, 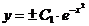 или
или  где
где  .
.
2) Найдем общее решение данного неоднородного уравнения в виде  .
.
Дифференцируя, имеем

Подставляя в данное уравнение выражения для у и y ', получим:


Отсюда
 , или
, или 
Откуда общее решение данного неоднородного уравнения: 
Метод Бернулли
Метод Бернулли предполагает, что общее решение линейного неоднородного уравнения (17) ищут в виде
y = u (x)× v (x), (21)
где u (x) и v (x) — неизвестные функции от x, одна из которых может быть выбрана произвольно. Найдем эти функции.
Дифференцируем (21):
 .
.
Подставим в уравнение (17) выражения для у и  , получим:
, получим:
 ;
;
 .
.
Так как одна из неизвестных функций, например u (x), может быть выбрана произвольно, то пусть u (x) — любое частное решение уравнения  . Пусть, например,
. Пусть, например,
u (x) =  .
.
Тогда имеем уравнение 
 . Решая его, получаем вторую функцию
. Решая его, получаем вторую функцию
 .
.
Возвращаясь к переменной у, находим общее решение линейного неоднородного уравнения (17):
y = u (x)× v (x) = 
 . (22)
. (22)
Пример 2. Найти общее решение уравнения  .
.
Решение. Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка. Разделив его на х, получим
р (х) = - 2/ х, q (x) =  .
.
Решим уравнение методом Бернулли.
Пусть y = u × v. Дифференцируем это выражение: 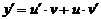 . Подставим в данное уравнение выражения для у и
. Подставим в данное уравнение выражения для у и  :
:
 .
.
Сгруппируем члены, содержащие u в первой степени, получим  . Полагаем
. Полагаем  , откуда
, откуда  . Интегрируя, находим
. Интегрируя, находим  или
или 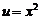 (постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).
(постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).
Для нахождения v имеем уравнение  . Это уравнение с разделяющимися переменными. Разделим его на
. Это уравнение с разделяющимися переменными. Разделим его на  :
:  . Проинтегрируем, получим
. Проинтегрируем, получим 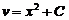 .
.
Таким образом, общее решение данного уравнения
y = uv =  .
.
Пример 3. Задача о переменном синусоидальном токе.
Пусть дана электрическая лампа, в которую включен источник периодического переменного тока. Найти закон изменения тока в зависимости от времени, если напряжение v изменяется по синусоидальному закону.
Решение. Примем за начальный момент времени  , при котором
, при котором  Тогда можно положить
Тогда можно положить 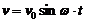 , где
, где  — частота.
— частота.
Уравнение изменения силы тока в электрической цепи с сопротивлением R и самоиндукцией L примет вид

Это линейное уравнение. Решаем его по общей формуле


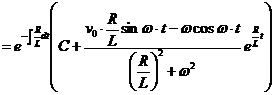 .
.
Здесь при нахождении интеграла  мы воспользовались формулой
мы воспользовались формулой
 .
.
Пример 4. Переходной процесс в электрической цепи.
В цепи с индуктивностью происходит переходный процесс. Индуктивность L и активное сопротивление R постоянны. Напряжение U задано как функция от времени t: U = f (t). Начальный ток равен  . Найти зависимость тока i от времени t. В частности, рассмотреть случай, когда
. Найти зависимость тока i от времени t. В частности, рассмотреть случай, когда 
Решение. Так как ток i в цепи изменяется со временем, то вследствие наличия индуктивности L возникает ЭДС самоиндукции

По закону Кирхгофа падение напряжения в цепи  равно сумме ЭДС. Таким образом,
равно сумме ЭДС. Таким образом,
 ,
,
или

- линейное неоднородное дифференциальное уравнение первого порядка.
По условию  , тогда получаем
, тогда получаем
 ,
,
или

Частным решением дифференциального уравнения, соответствующим начальному условию при t = 0,  , является функция
, является функция
 .
.
При  получим:
получим:
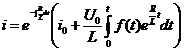 ,
,
или
 .
.
При возрастании t множитель  убывает, и через некоторое время процесс можно считать установившимся.
убывает, и через некоторое время процесс можно считать установившимся.
Ток будет определяться по закону Ома: 
Если 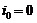 , то получим формулу для тока при замыкании цепи:
, то получим формулу для тока при замыкании цепи:
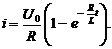
Из этой формулы видно,что ток i после включения батареи растет до значения  ,
,
так как ток  , называемый экстратоком замыкания, очень быстро убывает.
, называемый экстратоком замыкания, очень быстро убывает.
Если  то получим формулу затухающего тока при размыкании цепи
то получим формулу затухающего тока при размыкании цепи  . Этот ток называется экстратоком размыкания, с ростом t он стремится к нулю.
. Этот ток называется экстратоком размыкания, с ростом t он стремится к нулю.
Постоянная величина  называется постоянной времени цепи.
называется постоянной времени цепи.
Уравнение Бернулли
Дифференциальное уравнение первого порядка вида
y ' = p (x) ∙ y + q (x) ∙ ym, (24)
где m ¹ 0, m ¹ 1, p (x) и q (x) — заданные непрерывные функции, называется уравнением Бернулли.
Заметим, что при m = 0 уравнение (24) является линейным и решается, как указано в п. 1.4. При m = 1 (24) — уравнение с разделяющимися переменными и решается, как указано
в п. 1.1.
Уравнение Бернулли (24) обычно решают с помощью подстановки z = y 1- m (тем самым сводя его к линейному) или y = u × v (т.е. методом Бернулли).
Пример. Найти общее решение уравнения  .
.
Решение. Данное уравнение является уравнением Бернулли, где р (х) = 1/(х - 1) = q (x),
m = 2. Решим это уравнение разными способами.
1-й способ. Решим уравнение методом Бернулли. Пусть y = u × v.
Дифференцируем это выражение:
 .
.
Подставим в данное уравнение выражения для у и у':
 .
.
Сгруппируем члены, содержащие u в первой степени, получим
 .
.
Полагаем  , откуда
, откуда  .
.
Интегрируя, находим  , или
, или  (постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого уравнения).
(постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого уравнения).
Для нахождения v имеем уравнение  , откуда
, откуда 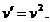 Это уравнение с разделяющимися переменными. Разделив переменные и проинтегрировав, получим
Это уравнение с разделяющимися переменными. Разделив переменные и проинтегрировав, получим 
Таким образом, общее решение данного уравнения

2-й способ. Решим уравнение с помощью подстановки  . Так как m = 2,то
. Так как m = 2,то  ,
,  ,
,  , подставляя в исходное уравнение выражения для у и dy, получим уравнение с разделяющимися переменными:
, подставляя в исходное уравнение выражения для у и dy, получим уравнение с разделяющимися переменными:
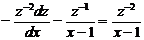 .
.
Разделим переменные:
 ,
,  ,
,

Проинтегрируем, получим  , откуда
, откуда
 .
.
Возвращаясь к переменной у, находим общее решение данного уравнения  , или после преобразований
, или после преобразований  , где
, где 
Уравнения в полных дифференциалах
Дифференциальное уравнение вида
М(x, y)  + N(x, y)
+ N(x, y)  = 0
= 0
называется уравнением в полных дифференциалах, если функции М (x, y) и N (x, y) удовлетворяют условию
 . (25)
. (25)
Из определения следует, что левая часть такого уравнения является полным дифференциалом некоторой функции F (x, y), а само уравнение имеет вид
dF (x, y) = 0.
Интегрируя его, видим, что решением уравнения в полных дифференциалах является функция F (x, y) = С.
Таким образом, решить уравнение в полных дифференциалах – значит найти функцию F (x, y), дифференциал которой
dF (x, y) = М (x, y)  + N (x, y)
+ N (x, y)  . (26)
. (26)
Найдем функцию F (x, y). Пусть для уравнения (7) выполняется условие (25), следовательно, и условие (26). Тогда
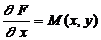 ,
, 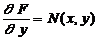 . (27)
. (27)
Интегрируем любое из уравнений (27), например первое (по х):
 , откуда F (x, y) =
, откуда F (x, y) =  .
.
Дифференцируем получившееся уравнение по у и приравняем его к правой части второго уравнения (27):

 = N (x, y).
= N (x, y).
Отсюда
 .
.
Интегрируя это уравнение по у, найдем С (у), а затем и общее решение уравнения в полных дифференциалах:
F (x, y) =  ,
,
где С (у) — уже известная функция.
Пусть для уравнения (7) условие (27) не выполняется. В некоторых случаях такое уравнение можно привести к уравнению в полных дифференциалах умножением на так называемый интегрирующий множитель. В общем случае он является функцией от х и у:  .
.
Если у данного уравнения существует интегрирующий множитель, зависящий только от х, то его находим по формуле
 ,
,
где выражение  должно являться функцией только от х.
должно являться функцией только от х.
Аналогично, множитель, зависящий только от у, находится по формуле
 ,
,
где выражение  должно являться функцией только от у.
должно являться функцией только от у.
Пример 1. Решить дифференциальное уравнение
(y + ex sin y) dx + (x + ex cos y) dy = 0.
Решение. Данное уравнение является уравнением в полных дифференциалах, т.к.
М (x, y) = y + ex sin y, N (x, y) = x + ex cos y,
 = 1 + ex cos y.
= 1 + ex cos y.
Рассмотрим уравнение
 = y + ex sin y.
= y + ex sin y.
Интегрируем его по х:
F (x, y) =  .
.
Дифференцируем получившееся уравнение по у и приравняем его к функции N (x, y):

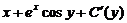 = N (x, y);
= N (x, y);
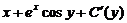 = x + ex cos y.
= x + ex cos y.
Отсюда С' (у) = 0, С (у) = С1. Общее решение уравнения в полных дифференциалах:
F (x, y) =  ,
,
или

где С = С 2 – С 1.






