М етод последовательных приближений (или метод Пикара) является аналитическим, т. е. позволяет получить приближённое решение задачи Коши, определяемой дифференциальным уравнением (1) с начальным условием (2), в виде формулы. Возник метод в связи с доказательством теоремысуществования и единственности решения задачи Коши (гл. 1).
Пусть в условиях данной теоремы требуется найти решение уравнения (1) с начальным условием (2). Проинтегрируем обе части уравнения (1) от х 0 до x:
 , откуда
, откуда
у (х) = у 0 + 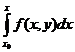 . (7)
. (7)
Очевидно, что решение интегрального уравнения (7) будет удовлетворять уравнению (1) и начальному условию (2). Действительно, при х = х 0 получим
у (х 0) = у 0 + 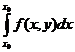 = у 0.
= у 0.
Применим к интегральному уравнению (7) метод последовательных приближений. Заменим в равенстве (7) неизвестную функцию у данным значением у 0, получим первое приближение
у 1(х) = у 0 +  .
.
Заметим, что интеграл в правой части содержит только одну переменную х, поэтому аналитическое выражение первого приближения у 1(х) будет являться функцией, зависящей
от х. Заменим теперь в равенстве (7) неизвестную функцию у найденным значением у 1(х), получим второе приближение
у 2(х) = у 0 + 
и т. д. В общем случае итерационная формула имеет вид
у n(х) = у 0 +  (n =1, 2,...). (8)
(n =1, 2,...). (8)
Применив неоднократно формулу (8), получим последовательность функций
у 1(х), у 2(х),..., у n(х),.... (9)
Можно доказать [1, 2, 3], что эта последовательность сходится и
 = у (х),
= у (х),
т.е. предел последовательности является решением интегрального уравнения (7), а следовательно, и дифференциального уравнения (1) с начальным условием (2). Это означает, что k -й член последовательности (9) является приближением к точному решению уравнения (1)
с определённой степенью точности.
Погрешность k -го приближения можно оценить формулой
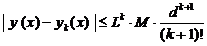 , (10)
, (10)
где L — постоянная Липшица; М — верхняя грань модуля функции f, т.е. 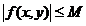 ;
;
величина d для определения окрестности 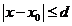 вычисляется по формуле
вычисляется по формуле  , числа а и b — из неравенства Липшица (гл. 1).
, числа а и b — из неравенства Липшица (гл. 1).
Пример 1. Найти три последовательных приближения решения дифференциального уравнения у' = x + y 2,удовлетворяющего начальному условию у (0) = 1.
Решение. В качестве начального приближения возьмём
у 0 = у (0) = 1,
тогда:
первое приближение у 1(х) = у 0 +  = 1+
= 1+  ,
,
второе приближение у 2(х) = у 0 +  = 1+
= 1+ 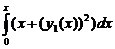 ,
,
третье приближение у 3(х) = у 0 +  = 1+
= 1+  .
.
Вычисления интегралов и построение графиков полученных функций у 1(х), у 2(х), у 3(х) проведём в системе MathCAD. Результаты решения представлены на рис. 14.
Оценим погрешность третьего приближения.
Для определения области G, заданной неравенствами (6), примем а = 1, b = 2. Получим
G: – 1  х
х  1,–1
1,–1  y
y  3.
3.
В прямоугольнике G функция
f (x, y) = x + y 2
определена и непрерывна, причём: 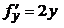 ,
,
 ,
,
 ,
,
 =
=  .
.
По формуле (10) получим
 .
.

|
Рис. 14
Заметим, что в программе MathCAD для вычисления интегралов с переменным верхним пределом интегрирования, необходимо выполнить следующие действия:
1) записать интеграл и выделить его в рамку;
2) выбрать команду Evaluate (Вычислить) из меню опции Simbolic (Символика) главного меню.
Существует и другой способ вычисления несобственных интегралов в программе MathCAD, по которому следует:
1) записать интеграл и выделить его в рамку;
2) выбрать команду Simplify (Упростить) из меню опции Simbolic (Символика) главного меню.
Пример 2. Найти пять последовательных приближений решения дифференциального уравнения
у' = х – 2 у,
удовлетворяющего начальному условию у (0) = 0.
Сравнить полученные приближения с точным решением.
Решение. В качестве начального приближения возьмём
у 0 = у (0)= 0.
Решение данного уравнения, проведённое в системе MathCAD, показано на рис. 15.

|
Рис. 15
МетодЭйлера
М етод Эйлера относится одновременно к численным и к графическим методам решения дифференциальных уравнений.
Суть метода заключается в том, что искомую интегральную кривую y = y (x) заменяют ломаной M0M1M2..., звенья которой являются касательными к интегральным кривым (рис. 16).


Рис. 16
Пусть требуется решить задачу Коши, т.е. найти решение дифференциального уравнения (1) с начальным условием (2) в виде функции y = y (x). Выбрав шаг h, построим, начиная
с точки х 0, систему равноотстоящих точек:
х i = х 0 + ih (i = 0, 1, 2, ...).
Вместо искомой интегральной кривой y = y (x) на отрезке [ х 0, х 1]рассмотрим отрезок касательной L 1 к ней в точке М0 (х 0, y 0). Уравнение касательной L 1, в силу (1), имеет вид
y = y 0 + f (х 0, y 0) (х – х 0).
При х = х 1 из уравнения касательной L 1 получим
y 1 = y 0 + hf (х 0, y 0),
откуда видим, что приращение функции на первом шаге имеет вид
 у 0 = hf (х 0, y 0).
у 0 = hf (х 0, y 0).
Аналогично, проводя касательную L 2 к некоторой интегральной кривой семейства в точке М1(х 1, y 1), получим
y = y 1 + f (х 1, y 1) (x – х 1).
При х = х 2 имеем y 2 = y 1 + hf (х 1, y 1), т.е. y 2 получается из y 1 добавлением приращения
 у 1= hf (х 1, y 1).
у 1= hf (х 1, y 1).
Таким образом, значения искомой функции y (x) могут быть определены по формулам:
yi +1 =yi +  у i,
у i,  у i = hf (х i, yi), (11)
у i = hf (х i, yi), (11)
где i = 0,1,2,..., которые называются вычислительными формулами метода Эйлера.
При этом искомую интегральную кривую y = y (x), проходящую через точку М0 (х 0, y 0), приближённо заменяем так называемой ломаной Эйлера M0M1M2..., звенья которой M i M i +1 прямолинейны между прямыми x = xi, x = xi +1 и имеют подъём
 .
.
Метод Эйлера является простейшим численным методом, удобным в применении, однако он имеет ряд существенных недостатков. Основной из них — малая точность. Она равна порядку h 2, причём с каждым шагом погрешность возрастает, т.е. происходит систематическое накопление ошибок. Поэтому на практике часто используют способ двойного счёта — с шагом h и с шагом h / 2. Совпадение десятичных знаков в полученных двумя способами результатах даёт естественные основания считать их верными.
Пример.
1. Найти методом Эйлера численное решение дифференциального уравнения
у' = x 3 + y,удовлетворяющее начальному условию у (0) = 1, на отрезке [0, 1] с шагом h = 0,1.
2. Найти точное решение уравнения у' = x 3 + y и сравнить его с приближённым на отрезке [0, 1].
Решение.
1. Для данного уравнения вычислительные формулы (11) имеют вид:
yi +1 =yi +  у i,
у i,  у i = 0,1(х i 3 + yi),
у i = 0,1(х i 3 + yi),
где i = 0,1,2,..., 10.
Учитывая, что погрешность метода имеет порядок h 2 = 0,01, достаточно в промежуточных результатах брать три цифры после запятой, а во всех yi сохранять только две цифры.
Результаты вычислений оформим в виде таблицы.
Таблица
| i | х i | yi |  yi = hf (х i, yi) = 0,1(х i 3 + yi) yi = hf (х i, yi) = 0,1(х i 3 + yi)
|
| 0 | 0 | 1 | 0,1 |
| 1 | 0,1 | 1,1 | 0,110 |
| 2 | 0,2 | 1,21 | 0,122 |
| 3 | 0,3 | 1,33 | 0,136 |
| 4 | 0,4 | 1,47 | 1,634 |
| 5 | 0,5 | 1,62 | 0,175 |
| 6 | 0,6 | 1,79 | 0,201 |
| 7 | 0,7 | 1,99 | 0,233 |
| 8 | 0,8 | 2,22 | 0,273 |
| 9 | 0,9 | 2,49 | 0,322 |
| 10 | 1 | 2,82 | — |
2. Данное уравнение у' = x 3 + y является линейным дифференциальным уравнением первого порядка. Решим его методом Бернулли.
Полагая y = uv, имеем
 = 0.
= 0.
Сгруппируем члены, содержащие u в первой степени, получим
 = 0.
= 0.
Полагаем  = 0, откуда
= 0, откуда  . Интегрируя, находим
. Интегрируя, находим  , или
, или  (постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).
(постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).
Для нахождения u имеем уравнение
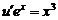 ,
,
или
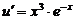 .
.
Разделим переменные, получим  , откуда
, откуда
 .
.
Интегрируем по частям три раза:


 .
.
Таким образом, общее решение данного уравнения
y = uv = 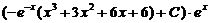 ,
,
или y =  .
.
Используя начальное условие у (0) = 1, получим 1 = ‑ 6 + С, откуда С = 7. Следовательно, искомое частное (точное) решение имеет вид
у =  .
.
Вычислим значения полученного точного решения на отрезке [0, 1] с шагом h = 0,1. Результаты округлим до 0,01 и запишем в таблицу.
Таблица
| i | х i | Приближённые значения yi | Точные значения y (х i) |
| 0 | 0 | 1 | 1 |
| 1 | 0,1 | 1,1 | 1,11 |
| 2 | 0,2 | 1,21 | 1,22 |
| 3 | 0,3 | 1,33 | 1,35 |
| 4 | 0,4 | 1,47 | 1,5 |
| 5 | 0,5 | 1,62 | 1,67 |
| 6 | 0,6 | 1,79 | 1,86 |
| 7 | 0,7 | 1,99 | 2,08 |
| 8 | 0,8 | 2,22 | 2,35 |
| 9 | 0,9 | 2,49 | 2,66 |
| 10 | 1 | 2,82 | 3,03 |
Сравнение приближённого (численного) решения данного дифференциального уравнения с точным на промежутке [0, 1] проведём с помощью системы MathCAD.
Результаты сравнения, а также численное решение данного уравнения, проведённое методом Эйлера в системе MathCAD, представлены на рис. 17.

|
Рис. 17
МодификацииметодаЭйлера
Существуют различные уточнения метода Эйлера, повышающие его точность. Цель модификаций — более точно определить направление перехода из точки (х i, yi) в точку (х i + 1, yi + 1). Так, метод Эйлера-Коши предлагает вычислять значения искомой функции y (x) по формулам:
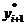 = yi + Д у i, Д у i = hf (х i, yi),
= yi + Д у i, Д у i = hf (х i, yi),
yi +1 = yi + h  , i = 0,1,2,....
, i = 0,1,2,....
Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке (х i, yi) и во вспомогательной точке (х i + 1, 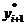 ). В качестве окончательного берём среднее этих направлений.
). В качестве окончательного берём среднее этих направлений.
Другой модификацией метода Эйлера является усовершенствованный метод ломаных, при котором сначала вычисляют промежуточные значения:
 ,
, 
и находят значение направления поля интегральных кривых в средней точке (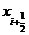 ,
,  ), т.е.
), т.е.  = f (
= f (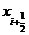 ,
,  ), а затем полагают
), а затем полагают
yi +1 = yi + h  .
.
Метод Эйлера и его модификации являются простейшими представителями конечно-разностных методов (шаговых методов) для приближённого решения задачи Коши.
Поскольку описанные методы предполагают повторяющиеся вычисления на каждом шаге, то они легко программируются и могут быть реализованы на компьютере.
На рис. 18 и 19 показаны решения дифференциального уравнения у' = x 3 + y,удовлетворяющего начальному условию у (0) = 1, полученные модифицированными методами Эйлера (методом Эйлера-Коши и усовершенствованным методом ломаных) с помощью системы MathCAD.

|
Рис. 18

|
Рис. 19
Метод Рунге-Кутта
Рассмотренный выше метод Эйлера относится к семейству методов Рунге-Кутта и является их простейшим частным случаем (методом первого порядка точности). Наиболее известным из методов Рунге-Кутта является классический четырёхэтапный метод четвёртого порядка точности. Его расчётные формулы для решения задачи Коши, определённой уравнениями (1) и (2), имеют вид:
yi +1 =yi +  у i;
у i;  у i =
у i =  (k 1(i) + 2 k 2(i) + 2 k 3(i) + k 4(i)), (12)
(k 1(i) + 2 k 2(i) + 2 k 3(i) + k 4(i)), (12)
где k 1(i)= h f (х i, yi);
k 2(i)= h f (х i +  , yi +
, yi +  );
);
k 3(i)= h f (х i +  , yi +
, yi +  );
);
k 4(i)= h f (х i + h, yi + k 3(i)), i = 0,1,2,....
Погрешность метода на каждом шаге является величиной порядка h 5.
Геометрический смысл использования метода Рунге-Кутта с вычислительными формулами (12) состоит в следующем (рис. 20).
 |
Рис. 20
Из начальной точки М 0(х 0, y 0) сдвигаются в направлении, определяемом углом  1, для которого tg
1, для которого tg  1= f (х 0, y 0). Идут в этом направлении на полшага, т.е. до вертикальной прямой
1= f (х 0, y 0). Идут в этом направлении на полшага, т.е. до вертикальной прямой
х = х 0 +  . На этом направлении выбирается точка Р 1с координатами
. На этом направлении выбирается точка Р 1с координатами

Затем из точки М 0(х 0, y 0)сдвигаются в направлении, определяемом углом  2, для которого tg
2, для которого tg  2 = f (х 0 +
2 = f (х 0 +  , y 0 +
, y 0 +  ), и на этом направлении выбирается точка Р 2с координатами
), и на этом направлении выбирается точка Р 2с координатами
 .
.
Далее из точки М 0(х 0, y 0) сдвигаются в направлении, определяемом углом  3, для которого tg
3, для которого tg  3 = f
3 = f  . На этом направлении выбирается точка Р 3с координатами
. На этом направлении выбирается точка Р 3с координатами
(х 0 + h, y 0 + k 3(0)). Этим задаётся ещё одно направление, определяемое углом  4, для которого tg
4, для которого tg  4 = = f (х 0 + h, y 0 + k 3(0)). Четыре полученных направления усредняются в соответствии с формулой
4 = = f (х 0 + h, y 0 + k 3(0)). Четыре полученных направления усредняются в соответствии с формулой
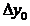 =
=  (k 1(0) + 2 k 2(0) + 2 k 3(0) + k 4(0)).
(k 1(0) + 2 k 2(0) + 2 k 3(0) + k 4(0)).
На этом окончательном направлении и выбирается очередная точка М 1с координатами (х 1, y 1) = (х 0 + h, y 0 +  ).
).
Теперь, уже исходя из точки М 1, все построения с помощью усреднений направлений повторяют сначала. Идут в новом усреднённом направлении до вертикальной прямой х = х 2, получают точку М 2(х 2, y 2) и т.д.
Эффективная оценка метода Рунге-Кутта затруднительна [2, 4]. Поэтому для определения правильности выбора шага h на практике обычно на каждом этапе из двух шагов применяют двойной пересчёт, а именно: исходя из текущего верного значения y (х i) вычисляют величину y (х i + 2 h) двумя способами: один раз с шагом h, другой раз — с двойным шагом 2 h.
Если расхождение полученных значений не превышает допустимой погрешности, то шаг h для данного этапа выбран правильно и полученное с его помощью значение можно принять за y (х i + 2 h). В противном случае шаг уменьшают в два раза.
На практике при вычислениях по формулам (15) обычно пользуются схемой, приведённой в таблице.
Таблица
| i | x | Y | k = hf (х, y) |  у у
|
| 0 | х 0
х 0 +  х 0 +
х 0 +  х 0 + h
х 0 + h
| y 0
y 0 +  y 0 +
y 0 +  y 0 + k 3(0)
y 0 + k 3(0)
| k 1(0) k 2(0) k 3(0) k 4(0) | k 1(0) 2 k 2(0) 2 k 3(0) k 4(0) |
| — | — | — | — | 
|
| 1 | х 1 | y 1 | ... | ... |
Пример. Найти методом Рунге-Кутта решение дифференциального уравнения у' = x 3 + y,удовлетворяющего начальному условию у (0) = 1, на отрезке [0, 1] с шагом h = 0,1.
Решение. Учитывая, что погрешность метода имеет порядок h 5 = 0,00001, в промежуточных результатах следует брать пять цифр после запятой, а во всех yi сохранять только четыре цифры. Результаты вычислений оформим в виде таблицы.
Таблица
| i | х | y | k = 0,1(х 3 + y) |  y y
|
| 0 | 0 0,05 0,05 0,1 | 1 1,05 1,0525 1,1053 | 0,1 1,10501 1,10526 1,11063 | 0,1 0,21003 0,21053 0,11063 |
| 0,1052 | ||||
| 1 | 0,1 0,15 0,15 0,2 | 1,1052 1,1604 1,1634 1,2219 | 0,11062 0,11637 0,11668 0,11136 | 0,11062 0,23278 0,21121 0,11136 |
| 0,10556 | ||||
| 2 | 0,2 0,25 0,25 0,3 | 1,2218 1,2717 1,2752 1,3399 | 0,12188 0,12874 0,12908 0,13669 | 0,12188 0,25747 0,25816 0,13669 |
| 0,12903 | ||||
| 3 | 0,3 0,35 0,35 0,4 | 1,3520 1,4081 1,4124 1,4853 | 0,13668 0,1451 0,14552 0,15493 | 0,13668 0,2902 0,29105 0,15493 |
| 0,14548 | ||||
| 4 | 0,4 0,45 0,45 0,5 | 1,4988 1,5628 1,568 1,6512 | 0,15493 0,16539 0,16591 0,17762 | 0,15493 0,33078 0,33182 0,17762 |
| 0,16586 | ||||
| 5 | 0,5 0,55 0,55 0,6 | 1,6661 1,74 1,7465 1,8425 | 0,17762 0,19064 0,19132 0,20585 | 0,17762 0,38128 0,38258 0,20585 |
| 0,19122 | ||||
| 6 | 0,6 0,65 0,65 0,7 | 1,8588 1,9618 1,9699 2,0826 | 0,20584 0,22199 0,2228 0,24082 | 0,20584 0,44399 0,4456 0,24082 |
| 0,22271 | ||||
| 7 | 0,7 0,75 0,75 0,8 | 2,0833 2,1855 2,1955 2,3268 | 0,24081 0,26074 0,26173 0,28388 | 0,24081 0,52148 0,52347 0,28388 |
| 0,26161 | ||||
| 8 | 0,8 0,85 0,85 0,9 | 2,3468 2,4898 2,5021 2,6585 | 0,28589 0,3104 0,31162 0,33875 | 0,28589 0,62079 0,62324 0,33875 |
| 0,31145 | ||||
| 9 | 0,9 0,95 0,95 1 | 2,6582 2,8545 2,8695 3,0566 | 0,34129 0,37119 0,37269 0,40566 | 0,34129 0,74238 0,74537 0,40566 |
| 0,37245 | ||||
| 10 | 1 | 3,0280 |
Соответствующее решение данного дифференциального уравнения, полученное методом Рунге-Кутта в системе MathCAD, представлено на рис. 21.

|
Рис. 21
Лабораторная работа
«Численные методы решения задачи Коши
для обыкновенных дифференциальных уравнений»
Задание 1.
1. Для заданного дифференциального уравнения первого порядка у' = f (x, y) c начальным условием у (a) = c найти приближённое решение в виде многочлена пятой степени.
2. Найти численное решение данного дифференциального уравнения на отрезке [ a, b ] с шагом интегрирования h, округляя результат до 0,001.
3. Найти точное решение заданного дифференциального уравнения у' = f (x, y) и сравнить его с приближённым на отрезке [ a, b ]. Построить графики полученных решений.
Исходные данные для 15-ти вариантов содержатся в таблице.
| Вариант | f (x, y) | a | b | с | h |
| 1 | 
| 0 | 1 | 0 | 0,1 |
| 2 | 
| 0 | 1 | 1 | 0,1 |
| 3 | 
| 0 | 2 | 0 | 0,1 |
| 4 | 
| p | 2p | 0 | p/10 |
| 5 | 
| 1 | 2 | 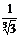
| 0,1 |
| 6 | 
| 1 | 3 | 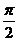
| 0,2 |
| 7 | 4 + 
| 1 | 2 | 2 | 0,1 |
| 8 | 
| 1 | 2 | 0 | 0,2 |
| 9 | 
| 0 | 2 | 0 | 0,1 |
| 10 | 
| 0 | 2 | 1 | 0,2 |
| 11 | 
| 1 | 2 | 0 | 0,2 |
| 12 | – 
| 0 | 1 | p/4 | 0,1 |
| 13 | – 
| 
| 
| е | 0,1 |
| 14 | 
| 0 | 1 | 1 | 0,1 |
| 15 | 
| 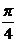
| 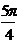
| 0 | 0,3 |
Указания к выполнению задания 1
1. Для того, чтобы получить приближённое решение заданного дифференциального уравнения в виде многочлена пятой степени, используйте формулу (3) при k = 0, 1,..., 5.
2. При выборе метода для вычисления точного решения учитывайте то, что дифференциальные уравнения вариантов 1- 4 являются линейными дифференциальными уравнениями, уравнение 5-го варианта — уравнение Бернулли, уравнения 6-8-х вариантов — однородные дифференциальные уравнения, а уравнения 9-15-х го вариантов — дифференциальные уравнения с разделяющимися переменными.
3. Для сравнения точного и приближённого решений заданного дифференциального уравнения сначала составьте таблицы их значений на отрезке [ a, b ], затем постройте на этом же отрезке графики полученных решений.
Задание 2. Решить задачу Коши для обыкновенного дифференциального уравнения первого порядка у' = f (x, y) на отрезке [ a, b ]при заданном начальном условии у (a) = c и шаге интегрирования h:
1) методом Эйлера с шагом 2 h и с шагом h;
2) модифицированным методом Эйлера (методом Эйлера - Коши или усовершенствованным методом ломаных);
3) методом Рунге-Кутта с шагом 2 h и с шагом h.
Результаты округлить до 0,0001. Сравнить полученные разными методами решения. Построить графики полученных решений.
| Вариант | f (x, y) | a | b | с | h |
| 1 | 2 – sin(x + y)2 | 2 | 3 | 2,3 | 0,1 |
| 2 | co s (1,5 x – y 2) – 1,3 | – 1 | 1 | 0,2 | 0,2 |
| 3 | cos(1,5 y + x 2) + 1,4 | 1 | 2 | 0,9 | 0,1 |
| 4 | cos(0,6 +y) + 2,5 x | 1 | 3 | 1,5 | 0,2 |
| 5 | 1,5 + sin(x + y) | 1,5 | 2,5 | 0,5 | 0,1 |
| 6 | 
| 2,6 | 4,6 | 1,8 | 0,2 |
| 7 |  +1 +1
| 0 | 2 | 2,9 | 0,2 |
| 8 | 
| 0 | 2 | 1 | 0,2 |
| 9 | 
| 0 | 2 | 0 | 0,2 |
| 10 | arcsin x+x – 
| 0 | 1 | 3 | 0,1 |
| 11 | 4,1 x – y 2 +0,6 | 0,6 | 2,6 | 3,4 | 0,2 |
| 12 | 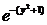 + 2 x + 2 x
| 0 | 0,5 | 0,3 | 0,05 |
| 13 |  + 2 y + 2 y
| 1,5 | 2 | 2,1 | 0,05 |
| 14 | 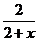 + x + 1 + x + 1
| 0,1 | 0,5 | 1,25 | 0,05 |
| 15 |  – 0,4 – 0,4
| 3 | 5 | 1,7 | 0,2 |






