Лекция 9. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В настоящее время разработано большое количество методов решения дифференциальных уравнений через элементарные функции, однако на практике эти методы бывают или совсем невозможны, или слишком громоздки. Поэтому для решения практических задач созданы методы приближенного решения дифференциальных уравнений. Условно эти методы делят на три группы в зависимости от формы представления решения:
— аналитические методы, дающие приближенное решение в виде аналитического выражения;
— графические методы, дающие приближенное решение в виде графика;
— численные методы, дающие приближенное решение в виде таблицы.
Ниже рассматриваются следующие методы решения обыкновенных дифференциальных уравнений: интегрирование дифференциальных уравнений с помощью формулы Тейлора, метод последовательных приближений (метод Пикара), метод Эйлера и его модификации, метод Рунге-Кутта.
Интегрирование дифференциальных уравнений с помощью степенных рядов
В некоторых случаях, когда интегрирование дифференциального уравнения точными методами невозможно, его решение ищут в виде степенного ряда:
y (x) =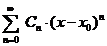 
.
Неопределённые коэффициенты С n находят подстановкой ряда в исходное уравнение, приравнивая коэффициенты при одинаковых степенях разности х – х 0в обеих частях полученного равенства. Если удаётся найти все коэффициенты ряда, то полученный ряд определяет решение во всей своей области сходимости.
Рассмотрим подробнее суть метода на примере решения обыкновенного дифференциального уравнения первого порядка.
Пусть задано обыкновенное, разрешённое относительно производной, дифференциальное уравнение первого порядка
у' = f (x, y) (1)
с начальным условием
у (х 0) = у 0. (2)
Пусть правая часть уравнения (1) является в точке (х 0, у 0) аналитической функцией, то есть может быть разложена в степенной ряд в некоторой окрестности этой точки. Тогда существует единственное решение y = y (x)заданного уравнения (1) с начальным условием (2). Это решение также будет являться аналитическим в точке х 0 и может быть представлено в виде ряда Тейлора:
y (x) =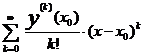 
, (3)
где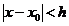 
, h — некоторое положительное число; k — целое неотрицательное число.
Значения производных у ( k )(х 0) в разложении (3) находят следующим образом: последовательно дифференцируют по х уравнение (1) у' = f (x, y)
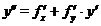, (4)
,
........................................
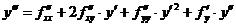подставляют начальное условие (2) в формулы (4):
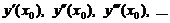
На практике ряд (3) обрывают на каком-либо члене и ищут приближённое решение в виде многочлена некоторой степени.
Аналогично с помощью ряда Тейлора можно интегрировать и дифференциальные уравнения высших порядков.
Пример.
1. Найти приближённое решение дифференциального уравнения у' = х – 2 у,удовлетворяющее начальному условию у (0) =0, в виде многочлена пятой степени.
2. Найти численное решение (в виде таблицы) данного дифференциального уравнения на [0, 1] с шагом h = 0,1, округляя результат до 0,001.
3. Найти точное решение и сравнить его с приближённым.
Решение.
1. Будем искать приближённое решение данного дифференциального уравнения в виде (3):
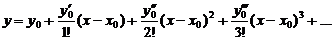
Так как у 0 = 0, тогда:
у 0 ' = 0;
;
;
;
.
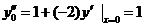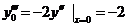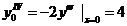Подставив найденные значения производных в уравнение (3), получим требуемое приближённое решение в виде многочлена пятой степени:
= 
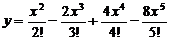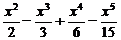. (5)
2. Найдём приближённое решение данного дифференциального уравнения в виде таблицы.
Подставив в решение (5) значения аргумента х из промежутка [0, 1] с шагом h = 0,1, получим численное решение данного уравнения на указанном промежутке. Запишем его, округляя результат до 0,001, в виде табл. 3.
Таблица3
| х | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
| у | 0 | 0 | 0,018 | 0,037 | 0,062 | 0,092 | 0,124 | 0,159 | 0,196 | 0,232 | 0,267 |
3. Найдём точное решение и сравним его с приближённым. Данное уравнение у' = х – 2 у, или у' + 2 у – х = 0,является линейным дифференциальным уравнением первого порядка. Решим его методом Бернулли.
Пусть y = u v, тогда имеем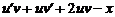 
= 0. Сгруппируем члены, содержащие u в первой степени, получим
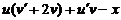= 0.
Полагаем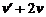 
= 0,
откуда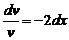 
.
Интегрируем:
,
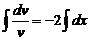откуда находим ln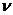 
= – 2 x Þ
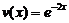
(постоянную интегрирования не вводим, так как достаточно найти какое-либо частное решение этого вспомогательного уравнения).
Для нахождения u имеем уравнение 
, или 
. Разделяем переменные:
,
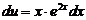интегрируем по частям:
.
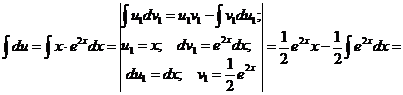
Таким образом находим функцию u (x):
.
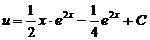Подставив найденные значения функций u = u (x)и v = v (x) в уравнение y = uv, получим общее решение данного уравнения:
y = uv = (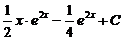
) 
= 
.
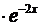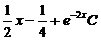Используя начальное условие у (0) = 0, получаем 0 = 
, откуда С =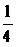 
.
Следовательно, искомое частное (точное) решение имеет вид
у =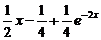 
. (6)
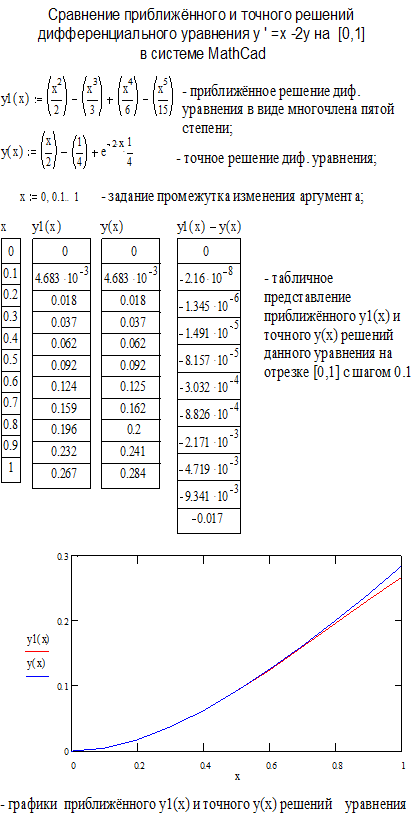
Сравнение приближённого решения (5) данного дифференциального уравнения с точным (6) на промежутке [0, 1] проведём с помощью компьютера. Для этих целей используем математическую систему MathCAD фирмы-разработчика MathSoft. 
Результаты сравнения представлены на рис. 13.
|
Рис. 13
