сопротивления металлов»
Цель работы: научиться пользоваться мостом для определения неизвестного сопротивления; определить температурный коэффициент сопротивления меди.
Приборы и принадлежности:
1. Мост для измерения сопротивления.
2. Калориметр.
3. Термометр.
4. Электрическая плитка.
5. Проводник неизвестного сопротивления.
Краткая теория
Проводники – вещества, обладающие способностью хорошо проводить электрический ток благодаря наличию в них большого числа свободных заряженных частиц.
К проводникам относят металлы, электролиты и плазму. Для определенности под проводником будем понимать металлическое тело.
В металлах (проводниках первого рода) носителями заряда являются квазисвободные электроны проводимости.
Электрическим током проводимости (электрическим током) называется упорядоченное (направленное) движение электрически заряженных частиц под действием электрического поля.
Количественно электрический ток характеризуется скалярной величиной - силой тока I и векторной величиной - плотностью электрического тока j.
Сила тока I - физическая величина, определяемая электрическим зарядом, переносимым через поперечное сечение проводника в единицу времени:
Электрический ток, направление движения электрических зарядов в котором и сила тока не изменяются со временем, называется постоянным.
Для постоянного тока
Единица силы тока – ампер (А).
Плотность электрического тока – векторная физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока:
, 
.
При равномерном распределении плотности электрического тока по сечению проводника сила тока в нем
,
где S – площадь поперечного сечения проводника.
В общем случае сила тока через поверхность S равна:
,
где 
- проекция плотности 
электрического тока на нормаль к площадке dS.
Вектор плотности электрического тока сонаправлен с вектором напряженности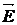 
электрического поля в данной точке, т.е. совпадает с направлением упорядоченного движения положительных зарядов. Поэтому за направление силы тока принимается направление упорядоченного движения положительно заряженных частиц.
Если концы проводника подсоединить к источнику напряжения, внутри проводника создается электрическое поле, действующее на свободные электроны с силой Кулона 
, сообщающей им ускорение 
.
Под действием этой силы электроны движутся с увеличением скорости до соударения с узлами кристаллической решетки, после чего скорость падает до нуля и процесс повторяется. Обозначив время между соударением за t, считая 
и 
, для средней скорости движения электронов, можно написать
(1)
Плотность тока
(2)
где 
- удельная электропроводность проводника, определяемая родом и состоянием его вещества;
n – концентрация заряженных частиц.
Соотношение 
выражает закон Ома в дифференциальной форме, так как характеризует состояние среды в одной точке.
Величина обратная удельной электропроводности проводника 
- называется удельным электрическим сопротивлением.
Из формулы (2), на примере однородного металлического проводника с одинаковым сечением S, длиной l, подставив 
, 
, 
, получим закон Ома в интегральной форме:
, (3)
где 
- электрическое сопротивление проводника. Единица сопротивления – ом [Ом].
Электрическое сопротивление характеризует способность проводника (электрической цепи) оказывать сопротивление движущимся в нем электрическим зарядам. Сопротивление зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан и температуры.
Если интервал изменения температуры достаточно мал, то зависимость сопротивления от температуры выражается формулой:
(4)
где 
- сопротивление проводника при температуре 0 °С,
- сопротивление проводника при t °C,
a - температурный коэффициент сопротивления.
Из формулы (4) следует, что
(5)
Температурный коэффициент сопротивления показывает, как изменяется каждая единица сопротивления проводника при изменении его температуры на один градус.
Единица измерения a - 
.
Температурный коэффициент сопротивления может быть как положительным, так и отрицательным.
У всех металлов сопротивление увеличивается с увеличением температуры и, следовательно, для металлов a>0.
Для чистых металлов a близок к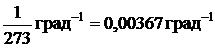 
, т.е. к температурному коэффициенту расширения газа.
При температуре 
сопротивление проводника
(6)
При температуре 
сопротивление проводника
(7)
Разделив уравнение (6) на (7), получим
(8)
Полученное выражение является рабочей формулой для вычисления a, так как она позволяет не определять 
(сопротивление при 0 °С). для определения a достаточно знать два сопротивления одного и того же проводника при любых различных температурах.
Описание установки
Для определения сопротивлений применяется особая схема, называемая мостом. Принципиальная схема моста изображена на рис. 1. В одну из диагоналей моста, между точками A и C, включена батарея E. В другую диагональ, между точками B и Д, включен чувствительный гальванометр Г. Для определения неизвестного сопротивления Rt нужно составить уравнения по законам Кирхгофа.
Назовем узлом любую точку разветвления цепи, в которой соединены более двух проводников, а ветвь – участок цепи между соседними узлами. Тогда можно сформулировать два закона Кирхгофа.
|
Рис. 1
I закон Кирхгофа. Алгебраическая сумма токов, сходящихся в узле, равна нулю
(9)
где 
– сила тока в проводнике;
n – число проводников, сходящихся в узле.
Условимся токи, подходящие к узлу, считать положительными, а отходящие – отрицательными.
II закон Кирхгофа. Алгебраическая сумма падений напряжений на участках замкнутого контура равна алгебраической сумме ЭДС в этом контуре:
, (10)
Замкнутый контур выбирается произвольно в разветвленной электрической цепи, где 
- число ветвей выбранного контура.
В схеме имеется 4 узла, следовательно, по первому закону Кирхгофа можно составить три независимых уравнения для токов в узлах. Для выбранных направлений токов (см. рис. 1)
(11)
По второму закону Кирхгофа составляем уравнения для трех независимых контуров: ABCEА, ABDA, BCDB.
(12)
Из шести уравнений системы (11) и (12) можно определить шесть неизвестных. Если известен ток 
, но не известно одно из сопротивлений, то неизвестное сопротивление может быть найдено решением системы уравнений. Такая схема называется неравновесным мостом.
Можно определить неизвестное сопротивление Rt проще, не прибегая к сложным подсчетам. Для этого пользуются равновесным мостом. плечи моста R 1, R 2, R 3 подбирают так, чтобы ток, проходящий через гальванометр, обратился в 0, то есть 
= 0. Это произойдет тогда, когда потенциалы точек B и D будут равны. При выполнении условия равновесия моста ( = 0):
, 
Отсюда получаем, что
; 
. (13)
Таким образом, в условиях равновесия моста неизвестное сопротивление Rt можно определить, зная сопротивление R 1 и отношение сопротивлений 
(см. формулу 13).
На лабораторном приборе отношения сопротивлений устанавливаются с помощью переключателя K, а сопротивление R 1 подбирается с помощью сопротивлений M 1, M 2, M 3, M 4 так, чтобы = 0 (рис. 2). На рис. 2: 1 - переключатель K; 2 – гальванометр Г; 3 – сопротивления M 1, M 2, M 3, M 4; Rt – неизвестное сопротивление. При этом R 1 , будет равно сумме сопротивлений M 1, M 2, M 3, M 4.
Неизвестное сопротивление представляет собой медную проволоку малого сечения, намотанную на картонный сердечник и помещенную внутрь стеклянной пробирки. В ходе работы пробирка с сопротивлением и термометром погружаются в калориметр с водой. Вода нагревается на электроплитке. Сопротивление медной проволоки измеряется с помощью моста при нескольких температурах.
Порядок выполнения работы
1. Подключить к зажимам Rt измеряемое сопротивление.
2. Переключатель схемы (4) поставить в положение “МВ”.
3. Ручкой “1” установить множитель “ n ” 
по таблице 1
Таблица 1
| Измеряемое сопротивление R t, Ом | Рекомендуемый множитель “ n ”
|
| 10 ¸ 99,99 | 0,01 |
| 100 ¸ 999,9 | 0,1 |
| 1000 ¸ 9999 | 1,0 |
| 10000 ¸ 50000 | 10,0 |
4. Уравновесить мост поворотом переключателей М1 – М4, чтобы I Г = 0.
Для этого:
а) поставить сопротивление М 1 в положение, соответствующее наибольшему сопротивлению (то есть 9000 Ом);
б) нажать на короткое время кнопку гальванометра с надписью «Грубо»;
в) заметив направление отклонения стрелки гальванометра, уменьшать сопротивление М 1 до тех пор, пока стрелка гальванометра не начнет отклоняться в противоположную сторону;
г) не изменяя сопротивления М 1, с помощью сопротивления М 2 добиваться, чтобы стрелка гальванометра все меньше отклонялась от нуля. Для этого повторяют действия, описанные в пунктах а) и в);
д) после того, как грубый подбор сопротивлений М 1 и М 2 сделан, на короткое время нажать на кнопку «Точно» и окончательно подобрать сопротивления M 2, M 3, M 4 так, чтобы = 0;
е) просуммировать сопротивления M 1, M 2, M 3, M 4.. Полученное сопротивление и есть R 1.
5. Вычислить сопротивление по формуле
,
где 
- множитель, устанавливаемый ручкой 1.
6. Для определения температурного коэффициента сопротивления измерить сопротивление Rt проводника через 5 °С 4¸5 раз (например, 20°, 25°, 30°, 35°, 40°С). Данные измерений занести в таблицу 2.
7. Вычислить температурный коэффициент сопротивления по формуле:
Результат занести в таблицу 2.
Таблица 2
|
№ п/п | Измерение | Вычисление | ||||
| t, °С | Rt, Ом | a | <a> | Da | <Da> | |
| 1. 2. 3. 4. | ||||||
8. Результат записать в виде
a = <a>±<Da>,
где 
Контрольные вопросы
1. Что такое электрический ток? Какая физическая величина характеризует электрический ток? Назвать единицу ее измерения.
2. Что такое плотность электрического тока? Как можно определить плотность тока? Единица измерения.
3. Чему равна удельная электропроводность? От каких величин она зависит?
4. Что такое удельное сопротивление проводника? От чего оно зависит?
5. Закон Ома в дифференциальной и интегральной форме.
6. Что такое сопротивление проводника? Единица измерения.
7. От чего зависит сопротивление металлического проводника при постоянной температуре?
8. Какова зависимость удельного сопротивления от температуры.
9. Как изменяется сопротивление металлов с повышением температуры? Почему? Какой закон выражает эту зависимость?
10. При каком условии мост находится в равновесии? Вывести формулу неизвестного сопротивления для равновесного моста.
11. Записать определяющую формулу для температурного коэффициента сопротивления. Можно ли в данной работе подсчитать по ней численное значение a?
12. Какой физический смысл имеет температурный коэффициент сопротивления a? Объяснить на полученном в работе результате.
13. вывести рабочую формулу для вычисления температурного коэффициента.
14. Пользуясь физическим смыслом a и его численным значением, взятым из работы, определить, на сколько изменится и каким станет сопротивление 25 Ом, нагретое на 10 °С от 0 °С.
15. Сформулировать и записать законы Кирхгофа.
16. Что называется узлом, ветвью, контуром?
Лабораторная работа № 5
«Определение удельного заряда электрона»
Цель работы: определить удельный заряд электрона методом магнетрона.
Приборы и принадлежности:
1. Триод
2. Амперметр
3. Соленоид
4. Потенциометр
5. Вольтметр
6. Соединительные провода
Краткая теория
Удельным зарядом электрона называется отношение величины заряда электрона к его массе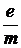 
. Это важнейшая характеристика заряженной частицы, определяющая заряд ее единицы массы. По ее величине можно вычислить массу заряженной частицы. Для измерения удельного заряда электрона используется метод скрещенных полей, получивший название метода магнетрона. Он заключается в том, что поток электронов пропускается через взаимно перпендикулярные электрическое и магнитное поля. На электрон, движущийся в этих полях, действует сила
где e – заряд электрона;
- скорость электрона;
- напряженность электрического поля;
- индукция магнитного поля.
При движении электрона в продольном электрическом поле на него действует сила Кулона 
. Эта сила совершает работу 
. За счет работы электрического поля изменяется кинетическая энергия электрона:
,
откуда
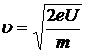, (1)
где U – разность потенциалов ускоряющего поля;
m – масса электрона.
Ускорившись в электрическом поле, электрон попадает в магнитное поле, перпендикулярное его скорости (поперечное поле).
На электрон в магнитном поле действует сила Лоренца, определяемая по формуле 
. Сила Лоренца направлена всегда перпендикулярно скорости движения частицы и сообщает ей нормальное ускорение (рис. 1 и 2).
 |
Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы, и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется. Под действием силы Лоренца в магнитном поле, направленном перпендикулярно скорости, электрон движется по окружности, т.е. сила Лоренца является центростремительной силой.
По второму закону Ньютона 
Так как 
то 
и
. (2)
Нормальное ускорение равно
, (3)
где R – радиус окружности.
Поэтому 
,
Откуда
. (4)
Подставив значение скорости из формулы (1) в уравнение (4), получим
(5)
радиус кривизны траектории электрона зависит от разности потенциалов электрического поля и индукции магнитного поля. При постоянной разности потенциалов электрического поля с увеличением индукции магнитного поля радиус кривизны траектории уменьшается. Измерив радиус окружности, по которой движутся электроны, из формулы (5) можно найти удельный заряд электрона:
. (6)
Описание установки
Экспериментальное определение 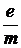для электрона осуществляется при помощи трехэлектродной лампы, помещенной в однородное магнитное поле. Схема подключения трехэлектродной лампы представлена на рис. 3.
Конструктивно анод этой лампы представляет собой цилиндр, вдоль оси которого натянута нить, являющаяся катодом лампы. Вокруг катода намотана спираль, являющаяся сеткой. Расстояние между сеткой и анодом равно r. Трехэлектродная лампа подключается так, что ее сетка соединяется с анодом. Благодаря этому электрическое поле существует только между катодом и сеткой и отсутствует между сеткой и анодом.
Рис. 3.
Электрон ускоряется электрическим полем, приобретает скорость
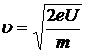
и движется прямолинейно по радиусу в пространстве между катодом и сеткой. Поперечное сечение трехэлектродной лампы показано на рис. 4.
При подачи на анод положительного потенциала в анодной цепи возникает ток, величину которого можно измерить амперметром A1.
Для создания магнитного поля лампу помещают внутри соленоида. При прохождении тока в цепи соленоида в нем возникает магнитное поле, индукция которого
, (7)
где I – ток в соленоиде, измеряемый амперметром А2 (см. рис. 3);
n – число витков на единице длины соленоида;
- относительная магнитная проницаемость среды;
- магнитная постоянная.
Электрон, попадая в поперечное магнитное поле между сеткой и анодом, начинает двигаться по кривой под действием силы Лоренца. Электроны продолжают при этом попадать на анод (см. рис. 4, а). С увеличением тока в соленоиде увеличивается индукция магнитного поля соленоида. Постепенно увеличивая индукцию и, следовательно, уменьшая радиус траектории электронов, можно добиться, чтобы при некотором значении 
электроны совсем не попадали на анод (см. рис. 4, б, в). тогда амперметр 
, включенный в цепь анода, покажет отсутствие тока.
При этом радиус окружности, по которой вращается электрон, должен быть меньше половины расстояния r между сеткой и анодом:
, (8)
Подставляем в формулу (6) значение радиуса (8) и индукцию (7), получаем
. (9)
Магнитная постоянная 
, а относительная магнитная проницаемость среды 
(электрон движется в вакууме). Подставив эти значения в формулу (9), получим следующую расчетную формулу для вычисления удельного заряда электрона
. (10)
Электроны, испускаемые нагретым катодом, обладают различными скоростями, поэтому критические условия достигаются для разных электронов при разных значениях индукции магнитного поля соленоида. Расчет 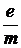ведется по величине тока соленоида, при котором большинство электронов не достигает анода. При этом наблюдается наиболее резкий спад анодного тока в триоде. Чтобы определить это значение тока I, строят график зависимости анодного тока 
от тока в соленоиде 
, откладывая по оси абсцисс ток в соленоиде, по оси ординат анодный ток.
График имеет резко спадающую часть, продолжая которую до пересечения с осью абсцисс, получим ток в соленоиде, при котором большинство электронов не попадает на анод (рис. 5).
Выполнение работы
1. Собрать электрические цепи по схемам (см. рис. 3).
2. Установить потенциометром постоянное напряжение на аноде.
3. Увеличивая ток в соленоиде от нуля, снять 5-7 значений анодного тока и соответствующих значений тока в соленоиде.
4. Данные измерения занести в таблицу 1.
Таблица 1
| № п/п | U, В | , мA
|  , A
|
5. Построить график зависимости анодного тока от тока в соленоиде и определить из графика значение тока соленоида, при котором большинство электронов не попадает на анод.
6. Вычислить удельный заряд электрона по формуле
,
7. Для проверки правильности результата вычислить относительную погрешность:
,
где 
- теоретическое значение удельного заряда электрона;
| e | = 1,6×10-19 Кл;
m = 9,1×10-31 кг;
- экспериментальное значение удельного заряда электрона.
8. При необходимости повторить эксперимент при другом постоянном напряжении на аноде.
Контрольные вопросы
1. Что такое удельный заряд электрона? Назвать единицу его измерения.
2. Что называется электростатическим полем? Каковы его характеристики?
3. Какая сила действует на электрон в электрическом поле, как она направлена?
4. Чему равна сила, действующая на заряд в магнитном поле? Как она направлена?
5. Объяснить физический смысл и назвать единицы измерения напряженности электрического поля и индукции магнитного поля.
6. Как выполняется лабораторная работа? Что нужно измерить и что вычислить?
7. Объяснить назначение основных элементов установки.
8. В каком поле движется электрон между катодом и сеткой; анодом и сеткой?
9. Как движется электрон в лампе (траектория и характер движения)? Какие силы действуют на электрон при его движении?
10. Существует ли электрическое поле между анодом и сеткой? Почему? С какой скоростью будет двигаться здесь электрон?
11. Что называется магнитным полем? Каковы его характеристики?
12. Как направлено магнитное поле соленоида относительно движения электрона? Как движется в нем электрон?
13. Изменяется ли скорость электрона при движении его в магнитном поле? Почему?
14. Когда ток в лампе станет равным нулю? Нужно ли добиваться этого? Почему?
15. От чего зависит радиус кривизны траектории электрона в поперечном магнитном поле?
16. Почему с возрастанием магнитного поля ток в лампе не мгновенно убывает до нуля?
17. Почему значение тока I находят, продолжая наиболее крутой участок графика?
18. Для чего строят график зависимости анодного тока от тока в соленоиде?
19. Каково условие исчезновения тока в электронной лампе под действием возрастающего магнитного поля?
20. Каково должно быть соотношение между радиусом траектории электрона и расстоянием от сетки до анода?
Лабораторная работа № 6
«Определение горизонтальной составляющей вектора напряженности и индукции магнитного поля Земли»
Цель работы:
1. Определить горизонтальную составляющую вектора напряженности и индукции магнитного поля Земли.
Приборы и принадлежности:
1. Магнитометр.
2. Компас.
3. Амперметр.
4. Реостат.
5. Двухполюсный переключатель.
6. Проводники.
7. Источник питания.
Краткая теория
Земля представляет собой огромный магнит. Схематически магнитное поле Земли представлено на рис.1.
В любой точке пространства, окружающего Землю и на её поверхности обнаруживается действие магнитного поля.
Основными характеристиками магнитного поля являются напряженность 
и индукция 
связанные между собой соотношением: 
, где m - относительная магнитная проницаемость среды. Для воздуха m = 1. - магнитная постоянная.
Если подвесить магнитную стрелку на нити так, чтобы точка подвеса совпала с центром тяжести стрелки, то стрелка установится по направлению касательной к силовой линии магнитного поля Земли, т.е. по направлению вектора индукции магнитного поля 
В северном географическом полушарии северный конец стрелки будет наклонен к Земле и стрелка составит с горизонтом угол наклонения j. На магнитном экваторе наклонение равно нулю. Вертикальная плоскость, в которой расположится стрелка, называется плоскостью магнитного меридиана.
Угол, который образует плоскость магнитного меридиана с географическим меридианом называется магнитным склонением или отклонением g.
Склонение – это угол между географическим и магнитным меридианами, т.е. между истинным направлением на север и тем, которое указывает магнитная стрелка.
Следы магнитных меридианов на поверхности Земли сходятся в магнитных полюсах N и S. Магнитные полюса не совпадают с географическими, поэтому магнитная стрелка отклонена от географического меридиана.
Южный магнитный полюс Земли расположен на севере. Он находится около берегов Северной Америки (71° с.ш. 96° з.д.), а северный магнитный полюс в Южном полушарии около берегов Антарктики (70° ю.ш. 150° в.д.). Магнитная ось не совпадает с осью вращения и не проходит через центр Земли.
Угол между осью вращения Земли и магнитной осью составляет угол 11,5°. Направление магнитных силовых линий на полюсах вертикальное по отношению к поверхности Земли, на экваторе – горизонтальное. Величина напряженности магнитного поля Земли очень мала около 0,5 эрстеда. 
.
Для сравнения: магнитное поле около полюса магнита, применяемого для школьных опытов, составляет несколько десятков эрстед.
 |
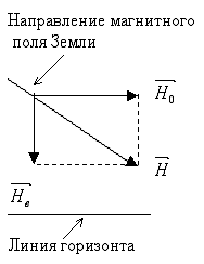Около полюсов величина напряженности магнитного поля вдвое превышает её величину на экваторе. Напряженность магнитного поля Земли в любой точке между экватором и полюсом можно рассматривать как векторную сумму вертикальной 
и горизонтальной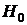 
составляющих (рис. 2).
Знание углов отклонения и наклонения, а также горизонтальной составляющей вектора напряженности 
дает возможность определить величину и направление полного вектора напряженности магнитного поля Земли в данной точке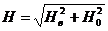 
.
Если магнитная стрелка может свободно вращаться лишь вокруг вертикальной оси, то она будет устанавливаться только под действием горизонтальной составляющей вектора индукции магнитного поля Земли в плоскости магнитного меридиана.
Горизонтальная составляющая 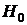, магнитное отклонение g и наклонение j называются элементами земного магнетизма. Все эти величины изменяются с течением времени.
Условились считать, что вектор магнитной индукции 
в произвольной точке поля совпадает по направлению с силой, которая действует на северный полюс бесконечно малой магнитной стрелки, помещенной в эту точку поля. Эта стрелка не искажает поле, в которое вносится. Сила, действующая со стороны магнитного поля на южный полюс стрелки, направлена в сторону, противоположную вектору 
. Следовательно, на стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпала с направлением поля, т.е. с направлением вектора .
Сила, действующая в веществе на пробную стрелку, называется магнитной индукцией ().
Магнитная индукция численно равна силе, действующей со стороны магнитного поля на единицу длины проводника с единичным током, расположенного перпендикулярно линиям индукции
Ее направление совпадает с направлением северного конца магнитной стрелки. Направление линии индукции можно определить, пользуясь правилом правого винта (обхвата правой руки). Линии магнитной индукции всегда замкнуты. Замкнутость линий индукции является выражением отсутствия в природе свободных магнитных зарядов.
Магнитное поле – одна из форм проявления электромагнитного поля, особенностью которого является то, что это поле действует на движущиеся в нем электрические заряженные тела и на тела, обладающие магнитным моментом, независимо от их состояния движения.
Описание установки
Установка состоит из магнитометра, представляющего собой катушку из большого числа витков, плотно прилегающих друг к другу, расположенных вертикально. В центре катушки помещается магнитная стрелка, вращающаяся вокруг вертикальной оси или компас.
При отсутствии тока в катушке магнитная стрелка располагается в плоскости магнитного меридиана под действием магнитного поля Земли.
Перед измерениями плоскость катушки совмещают с плоскостью магнитного меридиана. В этом случае один конец стрелки указывает на 0°, другой – на 180°.
Если по катушке пропустить ток, то в окружающем катушку пространстве возникает магнитное поле, вектор индукции которого в центре катушки будет направлен перпендикулярно к плоскости катушки. Таким образом, на стрелку будет действовать два взаимноперпендикулярных магнитных поля: магнитное поле Земли с напряженностью 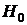и магнитное поле катушки напряженностью 
. Векторы напряженности этих полей взаимноперпендикулярны. Стрелка устанавливается по направлению результирующего вектора. На рис. 3 показано сечение катушки горизонтальной плоскостью (вид сверху). A и B – сечение витков катушки, NS – направление магнитного меридиана Земли, ns – магнитная стрелка, помещенная в центре катушки. 
- вектор горизонтальной составляющей магнитного поля Земли, 
- век-тор напряженности магнитного поля, созданного током в катушке.
Из рисунка видно, что 
, откуда
. (1)
На основании закона Био-Савара-Лапласа величина напряженности магнитного поля в центре кругового тока вычисляется по формуле
, (2)
где I – сила тока в катушке, измеряемая амперметром;
N – число витков катушки;
R – радиус витка.
Подставив выражение (2) в (1) получим
.
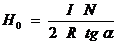Индукция вычисляется по формуле:
.
Выполнение работы
1. Собрать установку по схеме (рис. 4).
Рис. 4.
2. Установить плоскость катушки магнитометра в плоскости магнитного меридиана Земли.
3. Проверить установку, добившись чтобы при перемене направления тока в магнитометре разница в отклонениях магнитной стрелки не превышала двух градусов.
4. При помощи реостата подать в катушку ток определенного значения и измерить угол 
- отклонения магнитной стрелки.
5. Повторить опыт 3-4 раза при разных токах.
6. Изменить направление тока с помощью двухполюсного переключателя и повторить опыты с теми же значениями токов.
7. Занести данные измерений в таблицу 1.
8. Рассчитать для каждого тока горизонтальную составляющую напряженности магнитного поля Земли, используя значение 
.
9. Рассчитать среднее значение горизонтальной составляющей напряженности магнитного поля Земли и погрешность результатов измерений.
10. Вычислить относительную погрешность
.
11. Вычислить абсолютную погрешность
.
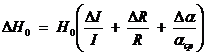12. Записать результат в виде
.
13. Вычислить среднее значение горизонтальной составляющей индукции магнитного поля Земли, используя соотношение 
.
14. Провести анализ результатов и сделать выводы.
Таблица 1
| № п/п | Измерения | Вычисления | ||||||||
| I А |
|
| 
| 
|
| 
| 
| 
| < B > Тл | |
Контрольные вопросы
1. Что такое магнитное поле? Как изобразить магнитное поле графически?
2. Физический смысл напряженности и индукции магнитного поля, единицы их измерения.
3. Как определить направление линий индукции магнитного поля?
4. Сформулировать и записать закон Био-Савара-Лапласа.
5. Используя закон Био-Савара-Лапласа, рассчитать напряженность и индукцию магнитного поля в центре кругового тока.
6. Какова цель работы и порядок выполнения.
7. Назначение составных частей установки и их работа:
а) как устанавливается магнитометр перед работой, почему?
б) как устанавливается магнитная стрелка до включения тока, после включения тока, почему?
в) зачем направление тока в магнитометре изменяют на противоположное?
г) как определить направление вектора индукции магнитного поля магнитометра?
д) что изменится, если магнитометр повернуть на 90°, как изменится положение магнитной стрелки при наличии тока, без тока?
е) какие поля и силы действуют на магнитную стрелку, если нет тока и при наличии тока в магнитометре?
8. Как вычислить горизонтальную составляющую индукции магнитного поля Земли.
9. Почему магнитная стрелка магнитометра должна быть малых размеров?
10. Как выполняется работа: что надо измерить и что вычислить?
Лабораторная работа № 7
«Построение петли гистерезиса методом Столетова»
Цель работы: исследовать зависимость магнитной индукции в ферромагнетике от напряженности магнитного поля.
Приборы и принадлежности
Основная схема:
1. Тороидальный трансформатор.
2. Баллистический гальванометр.
3. Ламповый реостат.
4. Амперметр.
5. Двухполюсный переключатель.
6. Соединительные провода.
Схема размагничивания тороида:
1. Автотрансформатор.
2. Реостат.
3. Источник ЭДС.
4. Соединительные провода.
Краткая теория
Всякое вещество является магнетиком, то есть способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле с индукцией 
, которое накладывается на обусловленное токами поле с индукцией 
. Оба поля в сумме дают результирующее поле (принцип суперпозиции):
. (1)
Для объяснения намагничивания тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствии внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается – его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле с магнитной индукцией 
.
Для характеристики магнетиков используется вектор намагниченности 
, магнитная проницаемость , магнитная восприимчивость 
.
В зависимости от направления и величины собственного магнитного момента вещества различают: диамагнетики, парамагнетики и ферромагнетики.
Диамагнетики характеризуются магнитной проницаемостью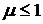 
, т.е. эти тела, внесённые в магнитное поле, ослабляют его. К диамагнетикам относятся медь, золото, серебро, цинк, свинец, висмут, т.е. тела, атомы и молекулы которых характеризуются близким к нулю магнитным моментом в отсутствии внешнего магнитного поля.
Парамагнетики характеризуются 
. Они несколько усиливают магнитное поле, обычно на сотые доли процента, если их внести в это поле. Собственный магнитный момент парамагнетиков направлен в ту же сторону, что и внешнее магнитное поле. К парамагнетикам относятся щелочные металлы, алюминий, кислород, азот.
Ферромагнетики – вещества,которые могут обладать магнитным моментом (быть намагниченными) даже в отсутствие внешнего магнитного поля. Для них 
. При внесении ферромагнетиков во внешнее магнитное поле они усиливают его во много раз. К ферромагнетикам относятся железо и его сплавы, в том числе широко используемые в постоянных магнитах алюминиево-никелевые стали, никель, кобальт, полупроводниковые соединения типа 
, называемые ферритами.
Описательная теория ферромагнетизма была разработана французским физиком П. Вейсом. Согласно представлениям Вейса в ферромагнетиках при температурах, не превышающих критических значений, характерных для каждого типа ферромагнетика и называемых точкой Кюри, существуют небольшие области с размерами 
м, самопроизвольно намагниченные до насыщения, это – магнитные домены. При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированны хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен.
Намагничивание слабомагнитных веществ (диамагнетиков и парамагнетиков) изменяется с изменением напряженности внешнего магнитного поля линейно.
Зависимость вектора намагниченности ферромагнетика и магнитной индукции 
от напряжённости внешнего магнитного поля 
определяется выражением:
, (2)
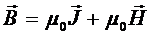, (3)
где 
- магнитная восприимчивость ферромагнетика;
– магнитная постоянная.
Магнитная индукция в слабых полях растет быстро с ростом , вследствие увеличения намагниченности ферромагнетика , а в сильных полях, поскольку слагаемое 
, 
растет с увеличением по линейному закону. На рис. 10.1 показана зависимость 
и 
.
 |
Рис. 1.
Характерная особенность ферромагнетиков состоит в том, что для них размагничивание отстает от намагничивания. Это явление получило название магнитного гистерезиса (рис. 1). Если довести намагничивание до насыщения (т.1 рис.1), а затем уменьшать напряженность внешнего магнитного поля, то уменьшение индукции следует не по первоначальной кривой 0-1, а изменяется в соответствии с кривой 1-2. В результате, когда напряженность внешнего поля станет равной нулю (т.2) намагничивание не исчезает и характеризуется величиной 
, которая называется остаточной индукцией.
Чтобы исчезла остаточная индукция в ферромагнетике, нужно создать внешнее магнитное поле, по направлению противоположное первоначальному.
Величина напряженности внешнего магнитного поля, при которой исчезает остаточная индукция, называется коэрцитивной силой 
(отрезок 0-3 рис. 1).
Если увеличивать напряженность отрицательного внешнего поля, то образец снова намагничивается; при этом намагничивание будет происходить по кривой 3-4 и ферромагнетик намагнитится в направлении противоположном первоначальному.
Уменьшая напряженность можно получить участок кривой 4-5 (см. рис. 1). Изменив направления намагничивающего поля и увеличивая его напряженность можно получить участок кривой 5-6-1.
Так получается замкнутая кривая, которая носит название петли гистерезиса.
Зависимость была впервые получена и подробно исследована русским ученым А.Г.Столетовым. Разработанный им баллистический метод измерения магнитной индукции будет использоваться в данной лабораторной работе.
