В лабораторной работе требуется получить основную кривую намагничивания (участок 0-1, см. рис. 1) и петлю гистерезиса для железного образца.
Исследуемый образец представляет собой тороид с железным сердечником и двумя обмотками: первичной и вторичной (рис. 2).

Рис. 2.
Первичная обмотка тороида служит для создания внешнего намагничивающего поля. Вторичная обмотка содержит 2-3 витка и служит для регистрации изменения магнитной индукции.
Напряженность намагничивающего поля в тороиде равна
 (4)
(4)
где  - ток в первичной обмотке тороида;
- ток в первичной обмотке тороида;
 - число витков первичной обмотки;
- число витков первичной обмотки;
 - длина средней линии тороида.
- длина средней линии тороида.
Из формулы (4) видно, что изменить  можно, изменяя ток в первичной обмотке.
можно, изменяя ток в первичной обмотке.
При изменении напряженности магнитного поля, созданного первичной обмоткой тороида, сердечник намагничивается, в результате чего изменяется индукция магнитного поля  .
.
Изменение индукции магнитного поля регистрируется с помощью баллистического гальванометра. Метод регистрации основан на явлении взаимной индукции. При изменении тока в первичной обмотке тороида изменяется магнитный поток, пронизывающий вторичную обмотку. Во вторичной обмотке при изменении магнитного потока возникает индукционный ток. По закону Фарадея - Ленца ЭДС электромагнитной индукции

где  - ЭДС индукции;
- ЭДС индукции;
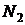 - число витков вторичной обмотки;
- число витков вторичной обмотки;
 - изменение магнитного потока.
- изменение магнитного потока.
Величина индукционного тока по закону Ома будет равна
 .
.
Ко вторичной обмотке тороида присоединен баллистический гальванометр. Величина отклонения зайчика гальванометра (отброс гальванометра) прямо пропорциональна величине заряда, прошедшего через гальванометр,
 ;
;
где  - заряд, прошедший через гальванометр;
- заряд, прошедший через гальванометр;
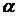 - отброс гальванометра;
- отброс гальванометра;
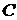 - баллистическая постоянная гальванометра.
- баллистическая постоянная гальванометра.
Величину заряда, прошедшего через гальванометр, можно найти, зная индукционный ток  ,
,
 ;
;  ;
;
 .
.
Изменение магнитного потока через вторичную обмотку
 ,
,
где  - площадь витка обмотки;
- площадь витка обмотки;
 - изменение магнитной индукции.
- изменение магнитной индукции.
 Тогда
Тогда
Отсюда видно, что
 . (5)
. (5)
Таким образом, при изменении тока в первичной обмотке возникает отброс гальванометра, пропорциональный изменению индукции магнитного поля в ферромагнетике.
Для изменения тока в первичной обмотке служит ламповый реостат (см. рис. 10.2). Ламповый реостат представляет собой набор ламп одинакового сопротивления, включенных параллельно. При включении одной лампы сопротивление цепи уменьшается и ток возрастает. Так как все лампы одинаковы, то при включении каждой лампы ток изменяется на одну и ту же величину, а значит, и магнитное поле тока тоже изменяется на одну величину
 .
.
Чтобы получить основную (начальную) кривую намагничивания, нужно иметь размагниченный образец, в котором одновременно  и
и  равны 0.
равны 0.
Для размагничивания образца нужно провести серию последовательных перемагничиваний, уменьшая каждый раз  - наибольшую напряженность магнитного поля. При этом получится серия петель гистерезиса, причем площадь каждой последующей меньше, чем предыдущей (рис. 3).
- наибольшую напряженность магнитного поля. При этом получится серия петель гистерезиса, причем площадь каждой последующей меньше, чем предыдущей (рис. 3).

Рис. 3.
Если плавно уменьшать  , то при
, то при  образец будет размагничен.
образец будет размагничен.
Практически можно осуществить размагничивание, если включить тороид в цепь переменного тока. При уменьшении величины переменного тока будет уменьшаться и напряженность  и с частотой 50 Гц изменяться направление напряженности магнитного поля. При
и с частотой 50 Гц изменяться направление напряженности магнитного поля. При  образец окажется размагниченным.
образец окажется размагниченным.
Выполнение работы
1. Размагнитить тороид. Для этого: а) включить первичную обмотку тороида в цепь переменного тока, содержащую амперметр и автотрансформатор (схема размагничивания); б) изменять с помощью автотрансформатора ток от 0 до  и от
и от  до 0.
до 0.
2. Собрать электрическую цепь по основной схеме (см. рис. 2).
3. Включить тороид в цепь, замкнув двухполюсный переключатель.
4. Следя за «зайчиком» гальванометра, включить первую лампу. Записать отброс  .
.
5. Записать отбросы гальванометра, включая последовательно одну за другой остальные лампы (первое зажигание; происходит намагничивание; участок 0-1, см. рис. 1).
6. Записать отбросы гальванометра, отключая одну за другой все лампы реостата в обратном порядке (на этом участке происходит уменьшение  и
и  ; участок 1-2, см. рис. 1).
; участок 1-2, см. рис. 1).
7. Изменить направление магнитного поля в тороиде, изменяя направление тока в первичной обмотке с помощью двухполюсного переключателя.
8. Записать отбросы гальванометра, включая одну за другой все лампы (второе зажигание; происходит намагничивание в направлении, противоположном первоначальному; участок 2-3-4, см. рис. 1).
9. Записать отбросы гальванометра, отключая одну за другой все лампы (второе гашение; происходит снова размагничивание образца; участок 4-5, см. рис. 1).
10. Еще раз изменить направление тока в первичной обмотке и записать отбросы гальванометра, включая последовательно все лампы (третье зажигание; происходит на этом участке намагничивание образца в первоначальном направлении; участок 4-6, см. рис. 1)
11. Данные измерений занести в табл. 1.
Таблица 1

| 
| 
| 
| 
| |
| Первое зажигание Первое гашение Второе зажигание Второе гашение Третье зажигание |
12. Построить по данным измерений график зависимости  . При построении графика вместо величины напряженности
. При построении графика вместо величины напряженности  можно отложить равные отрезки, так как
можно отложить равные отрезки, так как  , а при включении каждой лампы ток меняется на одну и ту же величину.
, а при включении каждой лампы ток меняется на одну и ту же величину.
Вместо индукции  можно откладывать по оси ординат отброс гальванометра (см. формулу 5), так как отброс гальванометра пропорционален изменению индукции магнитного поля
можно откладывать по оси ординат отброс гальванометра (см. формулу 5), так как отброс гальванометра пропорционален изменению индукции магнитного поля
 .
.
Для построения графика:
1. Отложить на оси абсцисс равные отрезки и пронумеровать полученные точки (номера отрезков должны соответствовать номерам ламп).
2. Отложить на оси ординат первый отброс  и построить точку 1 (ордината равна
и построить точку 1 (ордината равна  , абсцисса равна 1; включена одна лампа).
, абсцисса равна 1; включена одна лампа).
3. Ордината второй точки графика должна быть равна  ; абсцисса равна 2 (включены две лампы).
; абсцисса равна 2 (включены две лампы).
4. Каждая следующая точка графика строится путем добавления к предыдущей ординате следующего отброса гальванометра; абсцисса равна количеству включенных ламп (рис. 4, а).
5. Точки гашения строятся следующим образом: отброс гальванометра, полученный при гашении каждой лампы, вычитается из ординаты предыдущей точки; абсцисса равна числу включенных ламп (см. рис. 4, б).
Последняя точка гашения должна лежать на оси ординат (точка 2, см. рис.4, б).
6. При перемене направления магнитного поля во вторичной обмотке возникает большая ЭДС индукции и гальванометр дает большой отброс.

Рис. 4.
Для построения этой точки на графике нужно отброс  отложить от точки 2 вниз по оси ординат (отсчет вести от точки 2), абсцисса этой точки должна быть равна – 1, так как включена одна лампа.
отложить от точки 2 вниз по оси ординат (отсчет вести от точки 2), абсцисса этой точки должна быть равна – 1, так как включена одна лампа.
7. Остальные точки графика строятся аналогично (пункты 4-6).
Контрольные вопросы
1. Что такое магнитная проницаемость? Магнитная восприимчивость?
2. Классификация магнетиков по магнитной проницаемости.
3. Как ведут себя диа-пара- и ферромагнетики во внешнем магнитном поле?
4. Что такое магнитное насыщение? Как его получить?
5. Как зависит индукция магнитного поля в ферромагнетике от напряженности внешнего поля? (Объяснить по кривой намагничивания).
6. Что такое гистерезис? Объяснить на графике петли гистерезиса, что происходит в ферромагнетике на каждом участке кривой?
7. Что называется коэрцитивной силой? Остаточным намагничиванием? Показать на графике.
8. Как произвести полное размагничивание образца? Почему для этого используется переменный ток? Можно ли для этой цели использовать постоянный ток?
9. Чем отличаются по структуре ферромагнетики от диа- и парамагнетиков? Что такое домены?
10. Как создается намагничивающее поле в работе?
11. Единицы измерения: ε i, Н, В, m0,Ф.
Лабораторная работа № 8
«Определение индуктивности катушки и проверка закона Ома для электрической цепи переменного тока»
Цель работы:
1. Изучение явления самоиндукции
2. Определение индуктивности катушки без сердечника и с ферромагнитным сердечником
3. Проверка закона Ома для электрической цепи переменного тока
Приборы и принадлежности:
1. Катушка индуктивности
2. Ферромагнитный сердечник
3. Конденсатор
4. Реостат
5. Вольтметр
6. Амперметр
7. Источник переменного напряжения
8. Мост постоянного тока
Краткая теория
При изменении силы тока в проводящем контуре изменяется величина магнитного потока, сцепленного с этим контуром. Следовательно, в последнем, согласно закону Фарадея, будет индуцироваться электродвижущая сила (ЭДС). Возникновение индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. ЭДС самоиндукции пропорциональна скорости изменении силы тока в контуре
 (1)
(1)
Коэффициент пропорциональности L называется индуктивностью или коэффициентом самоиндукции и измеряется в генри (Гн). Индуктивность контура является мерой его «инертности» по отношению к изменению его силы тока и зависит от размеров контура, его геометрической формы, плотности намотки проводника и относительной магнитной проницаемости среды m, из которого изготовлен сердечник. Если электрическую цепь, содержащую последовательно соединенные резистор с омическим или активным сопротивлением R,катушку индуктивности L, и конденсатор электроемкости C, подключить к источнику переменного напряжения, то в такой цепи возникнет переменный электрический ток (рис. 1).

Рис. 1.
Пусть напряжение источника изменяется по гармоническому закону
 , (2)
, (2)
где  - амплитудное значение напряжения.
- амплитудное значение напряжения.
Тогда сила тока в цепи будет равна
 , (3)
, (3)
где  - амплитудное значение силы тока;
- амплитудное значение силы тока;
j - разность (сдвиг) фаз между приложенным напряжением и силой тока.
Падение напряжения на отдельных участках цепи определяются соотношениями
 (4)
(4)
где w - циклическая частота ( );
);
R – активное сопротивление;
 - индуктивное сопротивление;
- индуктивное сопротивление;
 - емкостное сопротивление.
- емкостное сопротивление.
В цепи переменного тока имеет место сдвиг по фазе между  и
и  , что можно представить на векторной диаграмме (рис.2) Колебания напряжения на емкости отстают по фазе от колебаний силы тока на
, что можно представить на векторной диаграмме (рис.2) Колебания напряжения на емкости отстают по фазе от колебаний силы тока на  , а колебания напряжения на индуктивности опережают колебания силы тока на
, а колебания напряжения на индуктивности опережают колебания силы тока на  . Напряжение на активном сопротивлении изменяется в синфазно с током.
. Напряжение на активном сопротивлении изменяется в синфазно с током.
|

Рис. 2.
Эффективные или действующие значения силы тока  и напряжения
и напряжения  связаны с амплитудными значениями переменного тока
связаны с амплитудными значениями переменного тока  и
и  соотношениями
соотношениями
 . (5)
. (5)
Закон Ома для RLC -цепи (рис.1) имеет вид
 , (6)
, (6)
где  - полное электрическое сопротивление (или импеданс); (7)
- полное электрическое сопротивление (или импеданс); (7)
R – активное (или омическое) сопротивление;
 - реактивное сопротивление (или реактанс) (8)
- реактивное сопротивление (или реактанс) (8)
Сдвиг по фазе между током в цепи и приложенным напряжением (рис.2) определяется соотношением
 (9)
(9)
В частном случае, если цепь переменного тока содержит лишь резистор R и катушку индуктивности L, формула (6) имеет вид

где  , откуда
, откуда
 . (10)
. (10)
Таким образом, для определения индуктивности катушки необходимо знать ее полное сопротивление Z, активное сопротивление R и циклическую частоту w переменного тока, которая связана с обычной частотой n соотношением  . Для промышленного тока частота
. Для промышленного тока частота  Гц.
Гц.
Порядок выполнения работы
Упражнение № 1
Определение индуктивности катушки.
1. Измерить с помощью моста постоянного тока активное сопротивление катушки R и определить погрешность D R.

Рис. 3.
2. Выбрать диапазоны и определить цену деления вольтметра и амперметра.
3. Собрать схему (рис. 3). Здесь A и V – амперметр и вольтметр, L – исследуемая катушка,  - потенциометр. К клеммам ab приложено переменное напряжение 220 В.
- потенциометр. К клеммам ab приложено переменное напряжение 220 В.
4. Замкнуть цепь и определить силу тока, идущего через катушку, для трех различных напряжений 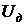 на ее концах.
на ее концах.
Вычислить Z по формуле  и найти среднее значение < Z>.
и найти среднее значение < Z>.
Вычислить абсолютную погрешность D Z по формуле
 ,
,
где D U и D I – соответственно приобретенные ошибки вольтметра и амперметра.
Найденные значения < Z>, < R> и w подставить в формулу (10) и определить искомую индуктивность < L>.
Определить абсолютную погрешность D L по формуле

5. Повторить опыт для одного значения напряжения 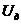 , вкладывая в катушку поочередно различные сердечники.
, вкладывая в катушку поочередно различные сердечники.
Найти индуктивность L с сердечником и вычислить абсолютную погрешность измерения D L (по п. 4).
6. Полученные результаты измерений и вычислений занести в таблицу 1.
Таблица 1
| U, В |
 ,
В ,
В
| I, мА |
 ,
мА ,
мА
|
 ,
Ом ,
Ом
| <Z>, Ом |
 ,
Ом ,
Ом
|
 ,
Ом ,
Ом
| L, Гн | D L, Гн | |
| Без сердечника | ||||||||||
| С сердеч- ником |
Результаты вычислений записать в виде:
 ;
;  - без сердечника;
- без сердечника;
 ;
;  - с сердечником;
- с сердечником;
Упражнение № 2
Проверка закона Ома для цепи переменного тока
1. Выполнить п.п.1 и 2 упражнения 1.
2. Собрать схему (рис. 4). Здесь A и V - амперметр и вольтметр, L – катушка индуктивности, C – конденсатор,  - потенциометр. К клеммам ab приложено переменное напряжение 220 В.
- потенциометр. К клеммам ab приложено переменное напряжение 220 В.

Рис. 4.
3. Замкнуть цепь и определить силу тока для трех различных значений напряжений 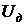 на ее концах.
на ее концах.
Вычислить Z по формуле  и найти среднее значение < Z>.
и найти среднее значение < Z>.
Вычислить абсолютную погрешность D Z по формуле
 ,
,
где D U и D I – соответственно приобретенные ошибки вольтметра и амперметра.
Результаты вычислений записать в виде:
 ,
, 
4. Вычислить Z по формуле (7) и записать результат.
5. Сравнить результаты п.п. 3 и 4 и сделать выводы.
Контрольные вопросы
1. Объяснить в чем состоит явление электромагнитной индукции, самоиндукции и взаимной индукции.
2. Сформулируйте основной закон электромагнитной индукции, эдс самоиндукции.
3. Дайте определение индуктивности.
4. Сформулируйте правило Ленца.
5. Дайте определение действующих значений напряжения и силы переменного тока.
6. Напишите формулы импеданса, реактанса цепи.
7. Дайте определение диа-, пара- и ферромагнетиков.
8. Объясните, в какую сторону и почему изменятся показания амперметра, если при неизменном напряжении в катушку ввести сердечник из: а) диамагнетика; б)парамагнетика; в) ферромагнетика?
9. Изобразите векторную диаграмму и с ее помощью определите сдвиг по фазе между током RLC -цепи и напряжением на ее концах.
10. сформулируйте закон Ома для цепи переменного тока, содержащей RLC -участки. Рассмотрите частные случаи.
11. Получите формулу для определения абсолютной погрешности D L.
Лабораторная работа № 9
«Построение петли гистерезиса»
Цель работы: исследовать зависимость магнитной индукции в ферромагнетике от напряженности магнитного поля.
Приборы и принадлежности
1. Тороидальный трансформатор;
2. Электронный осциллограф;
3. Понижающий трансформатор 220/42;
4. Источник питания (УИП-2, или делитель напряжения);
Краткая теория
Всякое вещество является магнетиком, то есть способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле с индукцией  , которое накладывается на обусловленное токами поле с индукцией
, которое накладывается на обусловленное токами поле с индукцией  . Оба поля в сумме дают результирующее поле (принцип суперпозиции):
. Оба поля в сумме дают результирующее поле (принцип суперпозиции):
 (1)
(1)
Для объяснения намагничивания тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствии внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается – его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле с магнитной индукцией  .
.
Для характеристики магнетиков используется вектор намагниченности  , магнитная проницаемость
, магнитная проницаемость  , магнитная восприимчивость
, магнитная восприимчивость  .
.
В зависимости от направления и величины собственного магнитного момента вещества различают: диамагнетики, парамагнетики и ферромагнетики.
Диамагнетики характеризуются магнитной проницаемостью 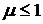 , т.е. эти тела, внесённые в магнитное поле, ослабляют его. К диамагнетикам относятся медь, золото, серебро, цинк, свинец, висмут, т.е. тела, атомы и молекулы которых характеризуются близким к нулю магнитным моментом в отсутствии внешнего магнитного поля.
, т.е. эти тела, внесённые в магнитное поле, ослабляют его. К диамагнетикам относятся медь, золото, серебро, цинк, свинец, висмут, т.е. тела, атомы и молекулы которых характеризуются близким к нулю магнитным моментом в отсутствии внешнего магнитного поля.
Парамагнетики характеризуются  . Они несколько усиливают магнитное поле, обычно на сотые доли процента, если их внести в это поле. Собственный магнитный момент парамагнетиков направлен в ту же сторону, что и внешнее магнитное поле. К парамагнетикам относятся щелочные металлы, алюминий, кислород, азот.
. Они несколько усиливают магнитное поле, обычно на сотые доли процента, если их внести в это поле. Собственный магнитный момент парамагнетиков направлен в ту же сторону, что и внешнее магнитное поле. К парамагнетикам относятся щелочные металлы, алюминий, кислород, азот.
Ферромагнетики – вещества,которые могут обладать магнитным моментом (быть намагниченными) даже в отсутствие внешнего магнитного поля. Для них  . При внесении ферромагнетиков во внешнее магнитное поле они усиливают его во много раз. К ферромагнетикам относятся железо и его сплавы, в том числе широко используемые в постоянных магнитах алюминиево-никелевые стали, никель, кобальт, полупроводниковые соединения типа
. При внесении ферромагнетиков во внешнее магнитное поле они усиливают его во много раз. К ферромагнетикам относятся железо и его сплавы, в том числе широко используемые в постоянных магнитах алюминиево-никелевые стали, никель, кобальт, полупроводниковые соединения типа  , называемые ферритами.
, называемые ферритами.
Описательная теория ферромагнетизма была разработана французским физиком П.Вейсом. Согласно представлениям Вейса в ферромагнетиках при температурах, не превышающих критических значений, характерных для каждого типа ферромагнетика и называемых точкой Кюри, существуют небольшие области с размерами  м, самопроизвольно намагниченные до насыщения, это – магнитные домены. При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированны хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен.
м, самопроизвольно намагниченные до насыщения, это – магнитные домены. При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированны хаотически и компенсируют друг друга, поэтому результирующий магнитный момент ферромагнетика равен нулю и ферромагнетик не намагничен.
Намагничивание слабомагнитных веществ (диамагнетиков и парамагнетиков) изменяется с изменением напряженности внешнего магнитного поля линейно.
Зависимость вектора намагниченности ферромагнетика  и магнитной индукции
и магнитной индукции  от напряжённости внешнего магнитного поля
от напряжённости внешнего магнитного поля  определяется выражением:
определяется выражением:
 , (2)
, (2)
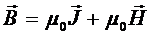 , (3)
, (3)
где  - магнитная восприимчивость ферромагнетика;
- магнитная восприимчивость ферромагнетика;

 – магнитная постоянная.
– магнитная постоянная.
Магнитная индукция  в слабых полях растет быстро с ростом
в слабых полях растет быстро с ростом  , вследствие увеличения намагниченности ферромагнетика
, вследствие увеличения намагниченности ферромагнетика  , а в сильных полях, поскольку слагаемое
, а в сильных полях, поскольку слагаемое  ,
,  растет с увеличением
растет с увеличением  по линейному закону. На рис. 1 показана зависимость
по линейному закону. На рис. 1 показана зависимость  и
и  .
.
Характерная особенность ферромагнетиков состоит в том, что для них размагничивание отстает от намагничивания. Это явление получило название магнитного гистерезиса (рис. 1).
Если довести намагничивание до насыщения (т.1 рис.1), а затем уменьшать напряженность внешнего магнитного поля, то уменьшение индукции следует не по первоначальной кривой 0-1, а изменяется в соответствии с кривой1-2.
 |
Рис. 1.
В результате, когда напряженность внешнего поля станет равной нулю (т. 2) намагничивание не исчезает и характеризуется величиной  , которая называется остаточной индукцией.
, которая называется остаточной индукцией.
Чтобы исчезла остаточная индукция в ферромагнетике, нужно создать внешнее магнитное поле, по направлению противоположное первоначальному.
Величина напряженности внешнего магнитного поля, при которой исчезает остаточная индукция, называется коэрцитивной силой  (отрезок 0-3).
(отрезок 0-3).
Если увеличивать напряженность отрицательного внешнего поля, то образец снова намагничивается; при этом намагничивание будет происходить по кривой 3-4 и ферромагнетик намагнитится в направлении противоположном первоначальному.
Уменьшая напряженность можно получить участок кривой 4-5 (см. рис. 1). Изменив направления намагничивающего поля и увеличивая его напряженность можно получить участок кривой 5-6-1.
Так получается замкнутая кривая, которая носит название петли гистерезиса.
Зависимость  была впервые получена и подробно исследована русским ученым А.Г.Столетовым. Разработанный им баллистический метод измерения магнитной индукции будет использоваться в данной лабораторной работе.
была впервые получена и подробно исследована русским ученым А.Г.Столетовым. Разработанный им баллистический метод измерения магнитной индукции будет использоваться в данной лабораторной работе.
Описание установки
Принципиальная схема лабораторной установки для изучения ферромагнетиков в переменном магнитном поле изображена на рис.2.
В качестве исследуемого образца используется ферромагнитный сердечник тороидального трансформатора Т, первичная обмотка которого питается от потенциометра Rn, подключённого к источнику переменного напряжения U = 42 В.

Возникающий при этом ток I 1 создаёт на сопротивлении R 1 падение напряжения Ux, связанное с напряжённостью магнитного поля Н трансформатора T соотношением
 ,
,  ,
,
где l 1 - длина первичной обмотки трансформатора Т (средняя длина тороидального сердечника);
I 1 - сила тока намагничивающего образец;
N1 - число витков первичной обмотки.
Таким образом, на вход Х осциллографа подаётся напряжение Ux, пропорциональное напряжённости Н магнитного поля тороидального трансформатора Т.
Для измерения магнитной индукции B в ферромагнитном сердечнике тороидального трансформатора Т применяется метод, основанный на законе электромагнитной индукции.
 .
.
Поскольку потокосцепление
y =В SN 2,
где S - сечение тороида;
N 2 - число витков вторичной обмотки трансформатора Т, то
 .
.
Следовательно, напряжение во вторичной обмотке пропорционально производной  . Для того чтобы подать на вход Y осциллографа Uy, пропорциональное В, необходимо между вторичной обмоткой трансформатора Т и входом Y осциллографа включить интегрирующую цепочку R2 C (рис.2). Действительно, преобразовав предыдущее выражение, получим
. Для того чтобы подать на вход Y осциллографа Uy, пропорциональное В, необходимо между вторичной обмоткой трансформатора Т и входом Y осциллографа включить интегрирующую цепочку R2 C (рис.2). Действительно, преобразовав предыдущее выражение, получим
 ,
,
 - закон Ома для переменного тока,
- закон Ома для переменного тока,
где I2 - ток во вторичной обмотке трансформатора T,
R2 - активное сопротивление (рис.2).
ЭДС самоиндукции вторичной обмотки считаем незначительной, т.к. число витков невелико.
R2 и С подобраны таким образом, что индуктивное и емкостное сопротивления пренебрежимо малы по сравнению с активным R2, тогда
e 2 = I 2 R и
 ,
,
где  - величина заряда на обкладках конденсатора С.
- величина заряда на обкладках конденсатора С.
Следовательно
 и
и  ,
,  .
.
Таким образом, напряжение Uy на конденсаторе С, подаваемое на вход Y осциллографа, пропорционально индукции магнитного поля В в ферромагнитном сердечнике тороидального трансформатора Т.
При подаче напряжения Ux на горизонтально отклоняющие пластины, а Uy - на вертикально отклоняющие пластины происходит сложение двух взаимно перпендикулярных колебаний электронного луча. В результате за полный период колебаний луч воспроизводит на экране осциллографа в определённом масштабе петлю гистерезиса, которая может служить основой для изучения магнитных характеристик ферромагнетиков.
Порядок выполнения работы
Подготовка установки к измерениям
1. Включить осциллограф, прогреть его 5...7 минут.
2. Установить ручки управления усилением входных сигналов осциллографа по осям «X» и «Y» в нулевое положение.
3. Электронный луч осциллографа сфокусировать в центр экрана.
4. Включить рабочую установку через понижающий трансформатор 220/42 в сеть и подключить её к осциллографу. Напряжения установки Ux и Uy подать соответственно к входам Х и Y осциллографа (при этом клеммы «Земля» осциллографа и установки соединяются между собой).
5. Ручку потенциометра Rn, установить в положение, соответствующее максимальному напряжению на первичной обмотке трансформатора T и получению насыщенной петли гистерезиса на экране осциллографа.
6. Ручками «Усиление» и «Синхр» добиться оптимального расположения насыщенной петли гистерезиса на экране осциллографа (при дальнейших измерениях эти ручки не трогать).
Проведение измерений
1. Измерить (в делениях шкалы по осям Х и Y) коэрцитивную силу  и остаточную магнитную индукцию
и остаточную магнитную индукцию  на полученной петле гистерезиса (
на полученной петле гистерезиса ( и
и 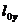 - длины сечения площади петли осью Х и Y). Результаты измерений занести в табл. 1.
- длины сечения площади петли осью Х и Y). Результаты измерений занести в табл. 1.
Таблица 1
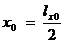 , дел. , дел.
| Ux 0, В | Н 0,

|  ,
дел. ,
дел.
| Uy 0, В | В 0, Тл |
2. Отключив усиление по оси Y (отсоединить установку от входа «Усиление Y» осциллографа), измерить длину отрезка lx 1, соответствующего сигналу на входе X. Тоже произвести с усилением по оси X, измерив длину отрезка ly 1 по оси У. Измеренные значения, х 1 и у 1 занести в табл. 2 (столбец «насыщение»,  ,
,  .
.
Таблица 2
| i | Насыщение | До насыщения | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |

| |||||||
| Uxi (B) | |||||||
Hi 
| |||||||

| |||||||
| Uyi (B) | |||||||
| Bi (Тл) | |||||||
| m i | |||||||
3. Уменьшая петлю гистерезиса с помощью потенциометра Rn установки, призвести такие же измерения lxi и lyi для пяти различных петель. Занести значения  ,
,  в табл. 2.
в табл. 2.
4. Произвести градуировку осциллографа.
Градуировка экранной сетки осциллографа
1. Отключить рабочую установку от осциллографа.
Таблица 3
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| Uxi (B) | ||||||

| ||||||
| Uyi (B) | ||||||

|
2. Подать на «Вход Х» напряжение Uxi от источника постоянного тока (делителя) и замерить длину lxi соответствующего ему сигнала на экранной сетке осциллографа. Результаты измерений  и Uxi занести в табл. 3 и построить градуировочный график
и Uxi занести в табл. 3 и построить градуировочный график 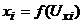 .
.
3. Аналогичные измерения провести по оси Y, подавая напряжения Uyi на «Вход Y» и замеряя длину l у i. Результаты  и Uyi занести в табл. 3 и построить зависимость
и Uyi занести в табл. 3 и построить зависимость  .
.
Обработка результатов измерений
1. Рассчитать напряженность Н i и магнитную индукцию В i по формулам
 , где
, где 
и
 , где
, где  .
.
Результаты расчетов занести в табл. 2.
 ,
,  - занести в табл. 1.
- занести в табл. 1.
2. Построить основную кривую намагничивания  по данным табл. 2.
по данным табл. 2.
3. Рассчитать относительное значение магнитной проницаемости по формуле  , занести эти значения в табл. 2 и построить график зависимости
, занести эти значения в табл. 2 и построить график зависимости  .
.
4. По графику  определить максимальное значение относительной магнитной проницаемости
определить максимальное значение относительной магнитной проницаемости  и ее начальное значение
и ее начальное значение  (a определяется по наклону касательной, проведенной в начальной точке кривой
(a определяется по наклону касательной, проведенной в начальной точке кривой  ).
).
5. Полученные характеристики ферромагнетика занести в табл. 4.
Таблица 4
| Данные | 
| 
| 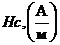
| В r, (Тл) |
| Лабораторные | ||||
| Справочные | ||||
| Отклонение |
Контрольные вопросы
1. Дайте определение напряженности и индукции магнитного поля. Какова связь между ними?
2. Дайте определение магнитной проницаемости. Дайте классификацию магнетиков: диамагнетики, парамагнетики, ферромагнетики.
3. Объясните поведение магнетика в переменном магнитном поле (магнитный гистерезис).
4. Объясните, от чего зависит площадь петли гистерезиса.
5. Объясните образование остаточной намагниченности.
6. Перечислите основные характеристики ферромагнетиков, их определение с помощью петли гистерезиса.
7. Опишите принципиальную схему установки для изучения явления гистерезиса.
Лабораторная работа № 10
«Исследование режимов однофазного трансформатора»
Цель работы: Изучить свойства однофазных трансформаторов путём экспериментальных исследований.
Программа работы
1. Выполнение опыта холостого хода
2. Выполнение опыта короткого замыкания
3. Исследование трансформатора под нагрузкой
4. Оформление отчёта






