вращательного движения»
Цель работы: с помощью маятника Обербека проверить опытным путем соотношение величин при вращательном движении.
Приборы и принадлежности:
1. Маятник Обербека.
2. Набор грузов.
3. Измерительная линейка.
4. Секундомер.
Краткая теория
Вращательным движением абсолютно твердого тела называется такое движение, при котором все точки тела описывают концентрические окружности с центрами, лежащими на одной прямой, называемой осью вращения.
Движение любой точки тела по окружности характеризуется следующими кинематическими величинами:
- угловой путь - это угол поворота радиуса вращения за время t; 
.
- угловая скорость - определяет изменение углового пути за единицу времени; 
.
- угловое ускорение – определяет изменение угловой скорости за единицу времени;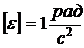 
.
Все эти величины одинаковы для каждой точки абсолютно твердого тела и не зависят от расположения точки относительно оси вращения тела. Вектор угловой скорости 
направлен по оси вращения согласно правилу правого винта (рис. 1). Вектор углового ускорения 
направлен также вдоль оси вращения в соответствии со знаком изменения углового ускорения 
(рис. 1).
Между линейными и угловыми величинами существует связь через радиус вращения материальной точки 
.
Линейный путь 
, то есть длина дуги окружности радиуса :
; (1)
линейная скорость:
; (2)
касательное ускорение:
; (3)
центростремительное ускорение:
. (4)
Опыт показывает, что изменение вращательного движения зависит не только от величины приложенной к нему силы, но и от точки приложения силы и направления ее действия. Для характеристики способности силы вызывать изменение вращения вокруг данной оси вводится понятие о моменте сил относительно оси.
Моментом силы 
относительно оси вращения называется векторное произведение радиуса – вектора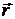 
, проведенного из точки О в точку приложения силы 
, на вектор силы :
.
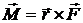Вектор всегда перпендикулярен плоскости, в которой лежат вектора 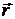и 
, то есть направлен вдоль оси вращения (направление определяется по правилу векторного произведения, или по правилу правого винта, или по правилу обхвата правой руки) (рис. 2, а).
Численное значение момента силы (рис. 2, б) 
, где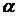 
- угол между векторам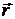и и . Из рис. 2, б 
, 
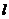- плечо силы - кратчайшее расстояние от оси вращения до линии действия силы. Таким образом,
(5)
Если направление действия силы параллельно оси вращения или пересекает ее, то такая сила не может изменить вращательное движение, так как в этих случаях момент силы 
.
Основным уравнением динамики вращательного движения является второй закон Ньютона, примененный к угловым характеристикам:
, (6)
где 
- главный момент всех внешних сил, действующих на тело;
- угловое ускорение;
- момент инерции тела относительно оси вращения.
Момент инерции есть мера инертности вращающегося тела относительно данной оси вращения.
Момент инерции материальной точки 
, где 
- масса материальной точки, 
- радиус вращения материальной точки.
Момент инерции тела зависит от распределения массы тела относительно оси вращения.
Момент инерции твердого тела равен сумме моментов инерции всех материальных точек, составляющих это тело:
.
Таким образом, формулировка основного закона динамики вращательного движения следующая:
Угловое ускорение, полученное вращающимся телом, прямо пропорционально суммарному (главному) моменту сил, действующих на это тело, и обратно пропорционально моменту инерции тела.
В лабораторной работе требуется проверить на опыте выполнение этого закона.
Согласно выражению (6) при постоянном значении момента силы (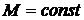
), но при разных значениях момента инерции тела:
,
отсюда 
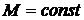при (7)
При постоянном моменте инерции (
), но при разных значениях моментов сил имеем:
.
Тогда 
при (8)
Соотношения (7) и (8) необходимо проверить в лабораторной работе.
Описание установки
Маятник Обербека (рис. 3) представляет собой маховик, состоящий из барабана Б, на который намотана нить с подвешенным к ней грузом Г. К барабану прикреплен диск Д с четырьмя навинчивающимися на него сплошными цилиндрами Ц.
Располагая цилиндры на диске на разном расстоянии от оси вращения и меняя их количество, изменяем момент инерции маятника Обербека, так как при этом изменяется масса и ее распределение относительно оси вращения.
Момент силы, действующей на обод барабана можно изменить, подвешивая к нити разные грузы. При этом изменяется сила натяжения нити, а следовательно, и момент силы. Рассмотрим вращательное движение маятника Обербека (рис. 3). Маятник вращается за счет того, что опускается груз Г и нить, намотанная на барабан Б, раскручивается. Таким образом груз Г движется поступательно вдоль оси ОУ с ускорением 
, а барабан Б с диском Д вращается с угловым ускорением 
. Для этих двух тел составим соответствующие уравнения движения.
1) 
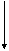На груз действует сила тяжести 
, направленная вниз (
- масса груза), и сила натяжения нити 
, направленная вверх. По второму закону Ньютона:
,
или проектируя на ось ОУ, получим:
(9)
2) На барабан действует по касательной к поверхности сила натяжения нити , которая и создает вращательный момент – момент силы. Плечом этой силы является радиус барабана. Согласно формуле (5)
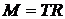. (10)
Из уравнения (9) получим силу натяжения нити 
, и тогда, с учетом формулы (10), момент силы относительно оси вращения:
. (11)
Из основного уравнения вращательного движения (6):
.
Поскольку ускорение 
, при условии, что нить не скользит по поверхности барабана, то из соотношения (3)
, (12)
и 
. (13)
Ускорение определяется из опыта. Так как на груз Г действуют постоянные силы, то движение груза равноускоренное. Тогда из формулы пути 
при начальной скорости 
, находим
, (14)
где 
- высота падения груза; 
- время его падения.
Выполнение работы
I. Четыре цилиндра по краям.
1. Установить четыре цилиндра на наибольшем расстоянии от оси вращения (положение С на рис. 3).
2. Подвесить к нити один груз (
), установить его на высоте 
от пола и измерить время его падения.
3. Подвесить к нити два груза (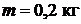
) и измерить время его падения также с высоты .
II. Четыре цилиндра ближе к центру.
1. Установить четыре цилиндра на расстоянии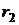 
от оси вращения.
2. Повторить пункты 2 и 3 части I.
3. Данные измерений занести в таблицу. Время падения грузов каждый раз измеряется три раза, вычисляется и записывается в таблицу среднее значение.
4. По формуле (14) вычислить линейное ускорение , по формуле (12) - угловое ускорение, а по формулам (11) и (13) - соответственно момент силы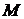 
и момент инерции . Результаты вычислений также занести в таблицу.
5. Выбрать в таблице примерно равные значения моментов силы, и для них проверить соотношение:
при .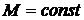
6. Выбрать в таблице примерно равные значения моментов инерции, и для них проверить соотношение:
при .
7. Результаты записать в таблицу.
8. Записать выводы, полученные в работе.
Таблица измерений и вычислений
, 
| Расположение цилиндров |
|
| 
| 
|
|
| 
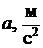
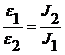при 
|  при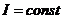 
|
| I.Четыре цилиндра по краям | 
|
|
| |||||
| II.Четыре цилиндра ближе к центру |
|
Контрольные вопросы
1. Какова цель данной работы?
2. Какое движение тела называется вращательным?
3. Какие кинематические величины характеризуют вращательное движение тела? Определить их физический смысл и единицы измерения.
4. Записать связь между линейными и угловыми кинематическими величинами. Каково направление каждой из этих величин?
5. Записать и сформулировать основной закон динамики вращательного движения. Дать определения физического смысла всех величин, входящих в это уравнение. Единицы их измерения.
6. Какая величина является причиной изменения угловой скорости? Почему ею не может быть только сила?
7. Как определить направление момента силы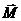 
?
8. Можно ли в данной работе изменить момент силы и как? Вывести расчетную формулу.
9. Почему в данной работе вращающая сила не равна силе тяжести груза?
10. Каким является движение опускающегося груза? Почему?
11. Каким является вращения диска? Почему?
12. Можно ли в данной работе изменить момент инерции диска и как?
13. Как в данной работе рассчитать момент инерции диска?
14. Какие соотношения проверяются в данной работе и при каких условиях?
15. Какие величины в данной работе измеряются, а какие вычисляются и по каким формулам?
Лабораторная работа № 3
