Лемма 5.1. Из m элементов a 1,…, an первой группы и n элементов b 1,…, bn второй группы можно составить ровно m ∙ n упорядоченных пар вида (ai, bj), содержащих по одному элементу из каждой группы.
(a1, b1), (a1, b2), …, (a1, bn), Всего m∙n пар 
(a2, b1), (a2, b2), …, (a2, bn), m строк
… … … … … …...
(am, b1), (am, b2), …, (am, bn).
n столбцов
Пример 5.2. В колоде карт 4 масти (черва, пика, трефа, бубна), в каждой масти по 9 карт или по 13 карт, тогда в колоде либо n=4∙9 =36 карт, либо n=4∙13=52 карты.
Лемма 5.3. Из n 1 элементов первой группы a 1, a 2,…,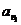 
,
n 2 элементов второй группы b 1, b 2,…,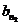 
,
и т.д. … … … … … … … …
nk элементов k -той группы x 1, x 2,…,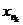 
.
можно составить ровно n 1 ∙ n 2 ∙…∙ nk различных упорядоченных комбинаций вида (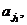
…, 
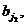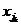), содержащих по одному элементу из каждой группы.
Пример 5.4. При бросании двух игральных костей число различных упорядоченных комбинаций следующее: N = 62 = 36; при бросании трех костей – N=63=216.
Леммы 5.1 и 5.3 называются основными правилами комбинаторики.
Пусть имеется множество из n элементов { a 1, a 2,…, an }. Будем рассматривать выборки объёма k вида (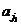
, 
, …, 
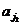) из n элементов. Все выборки можно классифицировать по двум признакам:
1) упорядоченные и неупорядоченные;
2) с возвращением и без возвращения.
Если выборки считаются упорядоченными, то играет роль порядок элементов в выборке. Если же выборка неупорядоченная, то все выборки с одним и тем же составом элементов отождествляются.
Пример 5.5. Рассмотрим множество, состоящее из трёх элементов {1,2,3}. Составим таблицу числа выборок объёма k =2 из трёх элементов.
| (1,1), (1,2), (1,3) (2,1), (2,2), (2,3) (3,1), (3,2), (3,3) | (1,1), (1,2), (1,3) (2,2), (2,3) (3,3) | с возвращением |
| (1,2), (1,3) (2,1), (2,3) (3,1), (3,2) | (1,2), (1,3) (2,3) | без возвращения |
| упорядоченные | неупорядоченные | выборки |
Общая таблица числа выборок объёма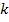 
из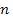 
элементов:
| nk |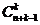 
| с возвращением |
| 
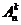
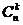
| без возвращения |
| упорядоченные | неупорядоченные | выборки |
Определение 5.6. Упорядоченная выборка без возвращения называется размещением.
Число размещений =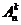 
.
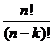Пример 5.7. В лифт 12-этажного дома зашли 3 человека. Найти вероятность того, что все вышли на разных этажах.
Ω={(i 1, i 2, i 3) | i 1, i 2, i 3 
{2,3,…,12}},{ i 1 
i 2, i 2 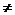i 3 } – 
дополнительное условие для события А. Первое (Ω – упорядоченные выборки с возвращением, n =113. Число благоприятствующих исходов k =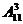 
= 
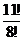=9∙10∙11. По классическому определению вероятности Р(А)= 
= 
= 
= 
. 
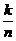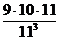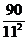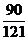Определение 5.8. Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке. Число перестановок из k элементов Pk = k! (0!=1).
Определение 5.9. Произвольное k -элементное подмножество множества, состоящего из n элементов, называется сочетанием из n элементов по k элементов.
Обозначается число сочетаний из n элементов по k элементов через
= 
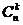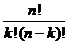; k 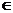{0,1,…, n }.
Свойства сочетаний:
1) 
= 
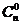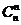=1;
2) 
= 
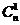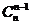= n;
3) = 
;
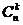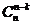4) 
+ = 
.
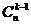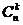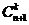