Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа

Теорема 11.1. (Пуассона) Пусть производится n независимых испытаний, в каждом из которых событие А наступает с вероятностью р. Тогда, если число испытаний неограниченно возрастает, а p →0, причём n ∙ p = a – величина постоянная, то P _n (k) .

По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях  

P _n (k)= 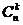p^kq^n-k= 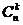p^k (1 - p) ^n-k.

Отсюда

P _n (k)= p^k (1 - p) ^n-k= p^k (1 - p) ^n-k.

По условию a = n ∙ p p = , подставляя, получим:

P _n (k)= =

= …  =

= … .

Переходя к пределу при n →∞

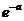= = [ т.к. ].

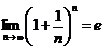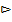
Замечание 11.2. Теоремой Пуассона удобно пользоваться, когда p →0, причём a = n ∙ p 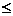10.Существуют специальные таблицы, в которых приведены значения вероятностей для различных параметров a и k.

Формула Бернулли удобна, когда значение n не очень велико. В противном случае используют приближенные формулы из теорем Муавра-Лапласа.

Теорема 11.3. (локальная теорема Муавра-Лапласа) Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т.е.0< p <1, то вероятность того, что событие A появится ровно k раз в n независимых испытаниях

P _n (k) , где – малая функция Лапласа, , q =1- p.

Имеются специальные таблицы значений функции 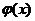. Нужно учитывать, что функция 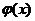– чётная, т.е. = .

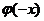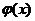Теорема 11.4. (интегральная теорема Муавра-Лапласа) Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от отлична от 0 и 1, т.е. 0< p <1, то вероятность того, что событие А появится от k ₁ до k ₂ раз в n независимых испытаниях, определятся выражением:

P _n (k ₁, k ₂) , где – функция Лапласа, , , q =1- p.

Функция Лапласа – нечётная, т.е. . Значения находят по таблице.

Пример 11.5. Пусть вероятность события А в каждом отдельном испытании p =0,8. Найти вероятность того, что событие А появится 75 раз в 100 независимых испытаниях.

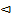 По локальной теореме Муавра-Лапласа х = = = –1,25. Значение (–1,25)= (1,25)=0,1826 находится по таблице.

Тогда вероятность

P₁₀₀(75) 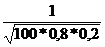*0,1826 0,04565.

Пример 11.6. Вероятность Р(А) появления события А в одном испытании равна 0,8. Найти вероятность того, что событие А появится более 69 раз в 100 независимых испытаниях.

  n =100, p =0,8, q =0,2, k ₁ = 70, k ₁ = 100.

По интегральной теореме Муавра-Лапласа 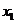= = = –1,25, 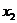= = = 5. По таблице (-2,5)= - (2,5)= -0,4938, (5)=0,5, P₁₀₀(70,100) (5) - (-2,5)=0,5+0,4938=0,9938

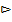
Случайные величины

Определение 12.1. Случайной величиной Хназывается функция Х(ω), отображающая пространство элементарных исходов Ω во множество действительных чисел 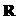. Т.о. Х(ω): Ω→ .

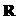Пример 12.2. Дважды подбрасывается монета. Рассмотрим случайную величину Х – число выпадений герба, определённую на пространстве элементарных исходов Ω={(г,г),(г,p),(p,г),(p,p)}. Множество возможных значений случайной величины Х-{0,1,2}. Составим таблицу

ω	(г,г)	(г,p)	(p,г)	(p,p)
Х(ω)	2	1	1	0

 

Одной из важнейших характеристик случайной величины является её функция распределения.

Определение 12.3. Функцией распределения случайной величины Хназывается функция F(x)=F _X (x) действительной переменной х, определяющая вероятность того, что случайная величина X примет в результате эксперимента значение, меньшее некоторого фиксированного числа х

F(x)=P{ X < x }=P{ X 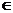(-∞; x)}.

Замечание 12.4. Если рассматривать случайную величину Х как случайную точку на оси O x, то функция распределения F(x) с геометрической точки зрения – это вероятность того, что случайная точка Х в результате реализации эксперимента попадёт левее точки х.

Свойства функции распределения

Свойство 12.5. Функция распределения F(x) – неубывающая функция, т.е.для  таких, что 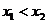 выполняется условие 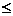F(x) F(x).

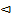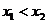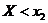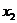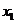Поскольку , то события { }={ }+{ }, по определению функции распределения F()=F()+P{ }.

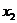Т.к. P{ } 0, то F()>F().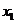

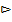
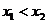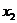Свойство 12.6. Для  таких, что  справедливо равенство P{ }= F()–F().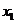

Замечание 12.7. Если функция распределения F(x) – непрерывная, то свойство 12.6 выполняется и при замене знаков 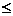 и < на < и .

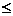Свойство 12. 8. 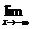  F(x)=0; F(x)=1.

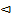  F(-∞)=P{ X < -∞ }=P(Ø)=0, F(+ ∞)=P{ X <+ ∞ }=P(Ω)=1.

Свойство 12.9. Функция распределения F(x) непрерывна слева ( F(x)=F()).

Свойство 12.10. P{ X x }=1-F(x).

{ X <+∞ }={ X < x }+{ X x }, по свойству вероятности  P{ X <+∞ }=P{ X < x }+P{ X x };

P(Ω)=1= F(x)+ P{ X x }, откуда P{ X x }=1- F(x).