| Рис. 3.1. Процесс передачи (1) и влияния (2) между цепями |
 Различают кабели симметричной и коаксиальной конструкций (рис. 2.2).
Различают кабели симметричной и коаксиальной конструкций (рис. 2.2).
Коаксиальная цепь представляет собой цилиндрическую трубку, внутри которой расположен изолированный от трубки проводник. Внутренний проводник и трубка (внешний проводник) являются проводами электрической цепи. Оба проводника имеют совпадающие геометрические оси. Электрические параметры их различны.
Симметричная цепь состоит из двух одинаковых по конструкции а электрическим параметрам изолированных проводников.
Передача электромагнитной энергии по кабелям характеризуется двумя явлениями: распространением энергии вдоль цепи и взаимным переходом энергии между цепями (рис. 3.1). Процесс распространения энергии вдоль цепи определяется параметрами передачи, а процесс взаимных переходов - параметрами влияния.
К параметрам передач и относятся:
1) первичные параметры цепи: R - активное сопротивление, L - индуктивность, С - емкость, G-проводимость изоляции;
2) вторичные параметры цели: α-коэффициент затухания, β - коэффициент фазы, Zв - волновое сопротивление, γ - коэффициент распространения электромагнитной энергии, v - скорость распространения электромагнитной энергии.
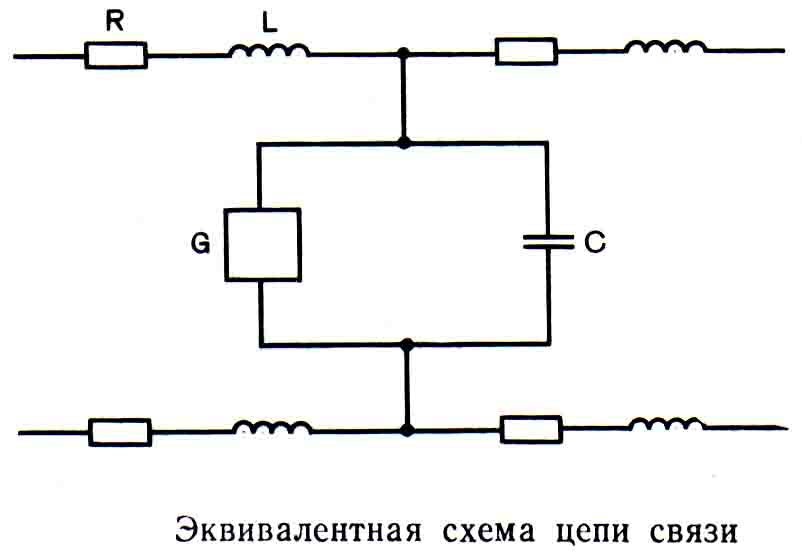
| Рис. 3.2. Эквивалентная схема цепи связи |
Все нормативы параметров для удобства расчетов и сравнения пронормированы на 1 км линии.
Активное сопротивление R - это сопротивление, которое испытывает переменный ток, проходя по цепи. Сопротивление R характеризует потери энергии в металлических частях кабеля на вихревые токи.
Активное сопротивление симметричной кабельной цепи переменному току, Ом/км,
R~= R0 + Rп.э + Rбл+Rм.

| Рис. 3.3. Явление поверхностного эффекта |
Сопротивление цепи постоянному току на длине в 1 км, Ом/км, определяется по формуле:

где d - диаметр проводника, мм; ρ - удельное сопротивление, Ом*мм2/м.
Вследствие скрутки проводников сопротивление цепи увеличивается пропорционально коэффициенту укрутки χ, значения которого в зависимости от диаметра кабеля приведены в табл. 3.1.
| Таблица 3.1. Коэффициент укрутки χ ффициент укрутки з ( | ||||||
| Диаметр повива, мм | до 30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Коэффициент укрутки | 1,010 | 1,016 | 1,025 | 1,037 | 1,050 | 1,070 |
Значения сопротивлений постоянному току двухпроводных кабельных цепей из медных и алюминиевых проводов при 20° С приведены в табл. 3.2.
| Таблица 3.2. Сопротивление постоянному току цепей из медных и алюминиевых проводников | |||||
|
Диаметр проводника, мм | Сопротивление проводника, Ом/км |
Диаметр проводника, мм | Сопротивление проводника. Ом/км | ||
| медного | алюминиевого | медного | алюминиевого | ||
| 0,32 0,4 0,5 0,6 0,7 | 445.0 285 190,0 131,6 96,0 | -- -- 317,0 218,0 160.0 | 0.8 0,9 -- 1.2 -- | 72.2 57,0 -- 31.9 -- | 120.0 94,7 -- 53.0 -- |
Кабельные цепи с алюминиевыми проводниками диаметром 1,15; 1,55 и 1,8 мм эквивалентны цепям с медными проводниками диаметром соответственно 0,9; 1,2 и 1,4 мм.
Сопротивление проводников, Ом/км, при температуре /, отличной от 20° С,

где R20 - сопротивление при t=20° С, Ом/км; αR - температурный коэффициент сопротивления; t - температура, при которой определяется сопротивление, 0С. Соотношение Rt/R20 для медных проводников приведено в табл. 3.3.
Сопротивление проводников возрастает за счет поверхностного эффекта и эффекта близости. Поверхностный эффект проявляется в вытеснении тока на поверхность проводника (рис. 3.3). Эффект близости обусловлен взаимодействием электромагнитных полей соседних проводников, в силу чего плотность тока перераспределяется, увеличивается на взаимно обращенных друг к другу поверхностях (рис. 3.4).
| Таблица 3.3. Соотношение для медных проводников | ||||||
| Температура, 0С | +50 | +45 | +40 | + 35 | +30 | +25 |
| Rt/R20 | 1,12 | 1,10 | 1,08 | 1,06 | 1,04 | 1,02 |
|
| ||||||
| Температура, 0С | +20 | + 15 | + 10 | +5 | 0 | -5 |
| Rt/R20 | 1,00 | 0,98 | 0,96 | 0,94 | 0,92 | 0,90 |
|
| ||||||
| Температура, 0С | -10 | - 15 | -20 | -25 | -30 | -35 |
| Rt/R20 | 0,88 | 0,86 | 0,84 | 0,82 | 0,80 | 0,78 |
Активное сопротивление кабельной цепи переменному току без учета Rм, Ом/км, определяется по формуле:


| Рис. 3.4. Эффект близости |
Дополнительное сопротивление, обусловленное потерями на вихревые токи в соседних проводниках и свинцовой (алюминиевой) оболочке, Ом/км,

где RT - сопротивление потерь в медных проводниках смежных четверок и свинцовой (алюминиевой) оболочке при f = 200 000 Гц, значения которого приведены в табл. 3.4.
| Таблица 3.4. Величины дополнительного сопротивления RT за счет потерь в медных проводниках смежных четверок,.свинцовой я алюминиевой оболочках | |||||||||||||
|
Число четверок в кабеле | Сопротивление потерь R, Ом/км | ||||||||||||
| смежные четверки для повивов | свинцовая оболочка для повивов | алюминиевая оболочка для повивов | |||||||||||
| первого | второго | третьего | четвертого | первого | второго | третьего | четвертого | первого | второго | третьего | четвертого | ||
| 1 | 0 | - | - | - | 22 | - | - | - | 8,1 | - | - | - | |
| 4 | 7,5 | - | - | - | 18 | - | - | - | 6,7 | - | - | - | |
| 1+6 | 8 | 7,5 | - | - | 1,5 | 5,5 | - | - | 0,6 | 2,0 | - | - | |
| 1+6+12 | 8 | 7,5 | 7,5 | - | 0 | 0 | 1,0 | - | 0 | 0 | 0,4 | - | |
| 1+6+12+18 | 8 | 7,5 | 7,5 | 7,5 | 0 | 0 | 0 | I,0 | 0 | 0 | 0 | 0,4 | |
Потери в алюминиевой оболочке меньше, чем в свинцовой, в 2,72 раза (√ σалюм/σсвинца = 2,72).
|
Таблица 3.5. Функции F, G, Н и Q для различных значений х | ||||
| х | F (х) | G(x) | h (х) | Q (х) |
| 0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 7,0 10,0 > 10,0 | 0 0,000326 0,00519 0,0258 0,0782 0,1756 0,318 0,492 0,678 0,862 1,042 1,743 2,799 (√2х-3)/4 | W/64 0,000975 0,01519 0,0691 0 1724 0,295 0,405 0,499 0,584 0,669 0,755 1, 109 1,641 (√2х-3)/8 | 0,0417 0,042 0,053 0,092 0,169 0,263 0,348 0,416 0,466 0,503 0,530 0,596 0,643 0,750 | 1,0 0,9998 0,997 0,987 0,961 0,913 0,845 0,766 0,686 0,616 0,556 0,400 0,282 2√2/х |
Индуктивность цепи L характеризуется отношением магнитного потока Ф к току I, создавшему этот поток:
L = Ф / I,
и состоит из наружной межпроводниковой индуктивности Lвн и внутренней индуктивности каждого проводника Iвн-
Индуктивность симметричной кабельной цепи, Г/км,

где а - расстояние между центрами проводников, мм; d - диаметр проводника, мм; % - коэффициент укрутки, значения которого приведены в табл. 3.1; Q(x) - коэффициент, значения которого даны в табл. 3.4.
| Таблица 3.6. Величины дополнительного сопротивления RT за счет потерь в медных проводниках смежных четверок,.свинцовой я алюминиевой оболочках | |||||||||||||
|
Число четверок в кабеле | Сопротивление потерь R, Ом/км | ||||||||||||
| смежные четверки для повивов | свинцовая оболочка для повивов | алюминиевая оболочка для повивов | |||||||||||
| первого | второго | третьего | четвертого | первого | второго | третьего | четвертого | первого | второго | третьего | четвертого | ||
| 1 | 0 | - | - | - | 22 | - | - | - | 8,1 | - | - | - | |
| 4 | 7,5 | - | - | - | 18 | - | - | - | 6,7 | - | - | - | |
| 1+6 | 8 | 7,5 | - | - | 1,5 | 5,5 | - | - | 0,6 | 2,0 | - | - | |
| 1+6+12 | 8 | 7,5 | 7,5 | - | 0 | 0 | 1,0 | - | 0 | 0 | 0,4 | - | |
| 1+6+12+18 | 8 | 7,5 | 7,5 | 7,5 | 0 | 0 | 0 | I,0 | 0 | 0 | 0 | 0,4 | |
В этой формуле первый член характеризует внешнюю индуктивность, а второй - внутреннюю. Внешняя индуктивность имеет наибольшее значение (порядка 60-90%). Внутренняя индуктивность по абсолютной величине значительно меньше внешней и с ростам частоты существенно снижается. Индуктивность цепей для различных типов кабелей приведена в табл. 3.7.
| Таблица 3.7. Индуктивность кабельных цепей | |||
| Назначение кабеля | Скрутка | Диаметр проводника, мм | Индуктивность, мГ/км |
| Городские сети Каблирование узлов и соединительные линии Междугородная связь | Парная Звездная | 0,5-0,7 0,8-1,4 1,2 | 0,6-0,55 0,75-0,7 0,82-0,78 |
Индуктивность искусственной цепи, образованной из четверки звездной скрутки, имеет примерно следующее значение в зависимости от индуктивности основной цепи: Lн = 0,7 LOCH, Г/км. Для четверки типа двойной пары Lн = 0,4LOCH, Г/км.
Емкость симметричной цепи, Ф/км, определяется по формуле:

где χ - коэффициент укрутки (см. табл. 2.1); ε - эквивалентная диэлектрическая проницаемость комбинированной изоляции; а - расстояние между центрами проводников, мм; d - диаметр проводника, мм; Ψ - поправочный коэффициент, характеризующий близость проводников заземленной оболочке и другим проводникам. Значения Ψ для различных скруток приведены в табл. 3.7.
| Таблица 3.8. Значения коэффициента Ψ для парной, звездной и двойной парной скрутки | |||
| d 1/ d 0 | Ψп | Ψз | Ψдп |
| 1,6 | 0,608 | 0,588 | 0,615 |
| 1.8 | 0,627 | 0,611 | 0,628 |
| 2,0 | 0,644 | 0,619 | 0,660 |
| 22 | 0,655 | 0,630 | 0,670 |
| 2,4 | 0,665 | 0,647 | 0,692 |
Примечание. d1 - диаметр изолированного проводника; d - диаметр проводника.
Эквивалентная диэлектрическая проницаемость зависит от типа изоляции, соотношения твердого диэлектрика и воздуха в изоляции кабеля и определяется выражением
є = (є1 S1 + є2 S2) / (S1 + S2),
где ε1 и ε2 - диэлектрические проницаемости соответственно первого и второго диэлектриков; S1 и S2 - площади поперечного сечения первого и второго диэлектриков.
| Таблица 3.9. Диэлектрическая проницаемость ε | ||
| Назначение кабеля | Изоляция | Значение ε |
| Городские сети | Бумагомассная Воздушно-бумажная Полиэтиленовая | 1,6-1,7 1,5-1,6 1,9-2,1 |
| Каблирование узлов и соединительные линии | Кордельно-бумажная Пористо-полиэтиленовая | 1,4-1,6 1,4-1,5 |
| Междугородная связь | Кордельно-бумажная Кордельно-стирофлексная Сплошная полиэтиленовая Пористо-полиэтиленовая Трубчато-полиэтиленовая | 1,3-1,4 1,2-1,3 1,9-2,1 1,4-1,5 1,2-1,3 |
| Таблица 3.10. Рабочая емкость кабельных целей | |||
| Назначение кабеля | Скрутка и изоляция | Диаметр проводника, мм | Емкость нф/км |
| Городские сети | Полиэтиленовая То же, с заполнением Воздушно-бумажная | 0,32…0,7 0,4…0,7 0,4…0,7 | 45±5 50±5 45…50 |
| Каблирование узлов и соединнтельные линии | Звездная с кордельно-бумажной изоляцией Звездная с пористо-полиэтиленовой изоляцией | 1.2 0,9 и 1,2 | 33-36 31-33 |
| Междугородная связь | Звездная с кордельно-бумажной изоляцией Звездная с кордельно-стирофлексной изоляцией Звездная с трубчато-полиэтиленовой изоляцией Звездная со сплошной полиэтиленовой изоляцией | 1,2 1,2 1,2 1,2 | 26,5 23,5 23,5 35,0 |
Значения эквивалентной диэлектрической проницаемости для различных кабелей приведены в табл. 3.8. В табл. 3.10 приведены значения рабочей емкости симметричных кабельных цепей. Емкость искусственной цепи, образованной иэ четверки звездной скрутки, в 2,7 раза больше емкости основной цепи, а при двойной парной скрутке - в 1,63 раза.
Проводимость изоляции G - это электрический параметр, характеризующий качество изоляции проводов кабеля. Проводимость изоляции обусловлена сопротивлением изоляции изолирующего материала, а также диэлектрическими потерями в кабеле и определяется по формуле, См/км,
G = G0 + G~
где Go = l/Rиз - проводимость изоляции постоянному току; Gf = ωCtg6 - проводимость изоляции, обусловленная диэлектрическими потерями при переменном токе. Величина сопротивления изоляции с увеличением температуры уменьшается. При температуре t (Rизt°), отличной от 20° С (Rиз20°),она рассчитывается по формуле:
Rизt0 = Rиз200 T
где Т - поправочный коэффициент.
| Таблица 3.11. Значения коэффициента Т при различной температуре | ||||||||
|
Вид изоляции | Температура, 0С | |||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | |
| Бумажная Стирофлексная | 2,46 1,02 | 1,82 1,01 | 1,35 1,00 | 1,00 1,00 | 0,74 1,00 | 0,55 0,99 | 0,41 0,99 | 0,30 0,98 |
Практические значения Rиз t°/Rиз 20° = Т для кабелей с различной изоляцией приведены в табл. 3.10.
В кабелях связи величина Go существенно меньше Gf и поэтому можно принять
G ≈ Gf = ω C tg δ,
где δ - эквивалентный угол диэлектрических потерь комбинированной изоляции. Величина tg δ для симметричных кабелей определяется по формуле:
tg δ = (ε1 tg δ1 S1 + ε2 tg δ2 S2) / (ε1 S1 + ε2 S2),
где ε1 и ε2 - диэлектрические проницаемости первого и второго диэлектриков; tg δ1 и tg δ2 - тангенсы углов диэлектрических потерь; S1 и S2 - площадь поперечного сечения соответственно первого и второго диэлектриков, например бумаги и воздуха.
Эквивалентные значения tg6 для симметричных кабелей с различными видами изоляции приведены в табл. 3.11.
| Таблица 3.12. Частотная зависимость tg б-10-4 для кабелей с различной изоляцией | ||||
|
Тип изоляции | Значения tg б 10-4 при частоте, кГц | |||
| 10 | 100 | 250 | 550 | |
| Кордельно-бумажная | 55 | 113 | 160 | 280 |
| Кордельно-стирофлексная | 3 | 7 | 12 | 20 |
| Сплошная полиэтиленовая | 2 | 6 | 8 | 14 |
| Пористо-полиэтиленовая | 3 | 8 | 12 | 20 |
| Балонно-полиэтиленовая | 2 | 6 | 8 | 12 |
Частотная зависимость первичных параметров кабельной цели показана на рис. 3.5. 
| Рис. 3.5. Зависимости первичных параметров цепи |
Волновое сопротивление ZB - это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, т. е. при условии, что на процесс передачи не влияют несогласованности на концах линии. Волновое сопротивление свойственно данному типу кабеля и зависит лишь от его первичных параметров и частоты передаваемого тока.
Величина ZВ, Ом, рассчитывается по формуле:

По своей физической природе величина ZB не зависит от длины кабельной линии и постоянна в любой точке цепи.
Электромагнитная энергия, распространяясь вдоль кабельной линии, уменьшается по величине и изменяется по фазе от начала к концу линии. Уменьшение или затухание энергии объясняется потерями ее в цепи передачи.
Коэффициент распространения электромагнитной энергии γ является комплексной величиной и может быть представлен суммой действительной и мнимой ее частей:

Действительная часть коэффициента распространения показывает уменьшение электромагнитной энергии в конце линии по сравнению с началом.
Мнимая часть выражения показывает изменение фазы (угла) при распространении энергии по цепи.
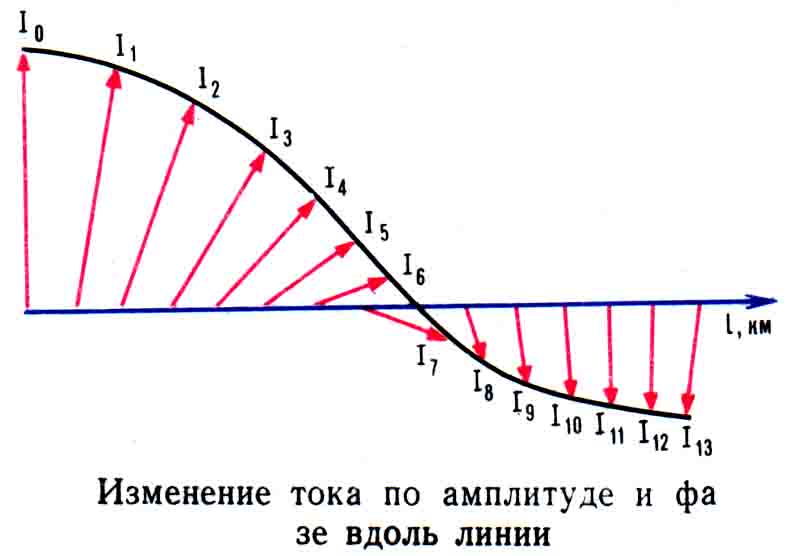
| Рис. 3.6. Изменение тока по амплитуде и фазе вдоль линии |
При передаче сигналов связи параметры α и β характеризуют соответственно затухание и изменение фаз тока, напряжения и мощности на участке кабельной цепи длиной 1 км и называются коэффициентом затухания и коэффициентом фазы.
Коэффициент распространения γ = α + j·β одновременно определяет изменение сигнала как по абсолютной величине, так и по фазе на 1 км длины кабеля.
Затухание в 1 дБ характеризует уменьшение по мощности в 1,26 раза, а по току или напряжению в 1,12 раза.
Между неперами и децибелами существует следующее соотношение: 1 Нп = 8,686 дБ или 1 дБ = 0,115 Нп.
Коэффициент фазы β измеряется в радианах или градусах на 1 км (1 рад =57,3°).
Характер изменения тока вдоль однородной кабельной линии показан на рисунке. Как видно из графика, вектор тока уменьшается и изменяет фазу вдоль линии. Уменьшение тока происходит по экспоненциальному закону.
Затухание кабельных цепей с повышением температуры несколько увеличивается. Коэффициент затухания, дБ/км, кабельной цепи при температуре, отличной от 20° С, определяется по формуле:
αt = α20 + [1 + αα(t-20)]
где α20 - коэффициент затухания при температуре 20° С; а αα коэффициент затухания.

| Рис. 3.7. Скорость распространения энергии по кабелю |
v = ω / β
На рис. 3.7 представлена частотная зависимость скорости распространения электромагнитной энергии по кабельным линиям. При постоянном токе она составляет примерно 10 000 км/с, а при токах высоких частот имеет величину порядка 200 000 км/с. Скорость распространения энергии по коаксиальным кабелям больше, чем по симметричным.
Вторичные параметры кабельных линий можно рассчитывать с достаточной точностью по сокращенным формулам.
При постоянном токе (f =0)
 ; β=0;
; β=0; 
В диапазоне низких частот (f ≈ 800 Гц)
 ;
; 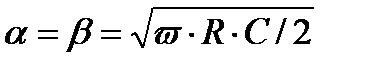 ;
; 
При высокочастотной передаче
 ;
;  ;
;  .
.

| Рис. 3.8. Частотная зависимость коэффициента затухания α и коэффициента фазы β кабельной цепи |

| Рис. 3.9. Частотная зависимость волнового сопротивления кабельной цепи |
Отличие цепей воздушных линий (ВЛС) от кабельных состоит в том, что на ВЛС провода расположены друг от друга (a/r ≈ 50) и можно не учитывать эффект их близости и воздействие окружающих масс.
Активное сопротивление, Ом/км, цепи воздушной линии состоит из сопротивления постоянному току и сопротивления за счет поверхностного эффекта
R = R0 + Rп.э. = 2 R0 [1 + F(x)]
где R0 = 4000 ρ / π d2 – сопротивлении постоянному току; d = 2 r – диаметр провода; х – коэффициент вихревых токов.
Индуктивность, Гн/км, состоит из внешней и внутренней индуктивностей
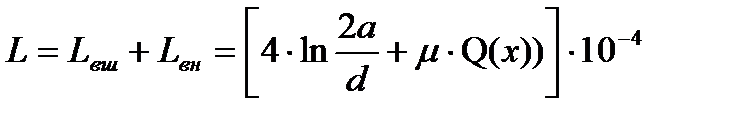
где а – расстояние между проводами; Внешняя индуктивность существенно больше внутренней. В области высоких частот действует только внешняя индуктивность.
Емкость, нФ/км, определяется формулой
С = 1,05*10-6 / (36 ln (a/r))
Коэффициент 1,05 учитывает увеличение емкости цепи за счет наличия изоляторов и соседних проводов.
Проводимость изоляции, См/км, цепей воздушных линий зависит как от частоты передаваемого тока, так и от состояния погоды и изоляторов на линии.
Проводимость рассчитывается по формуле
G = G0 + nf,
где G0 – проводимость изоляции при постоянном токе, равная 1/Rиз; n – коэффициент, учитывающий потери в диэлектрике при переменном токе.
При сухой погоде принимают G0 = 0,01*10-6 См/км и n = 0,05, а для сырой погоды G0 = 0,5*10-6 См/км и n = 0,25.


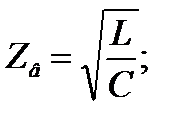

Параметры коаксиальной цепи.
Активное сопротивление равно сумме активных сопротивлений внутреннего и внешнего проводов, при t = 200С и определяется по формуле:

где d – диаметр внутреннего проводника, мм
D – диаметр (внутренний) внешнего проводника, мм.
Индуктивность коаксиальной цепи равна сумме двух индуктивностей: межпроводной индуктивности и внутренней индуктивности проводов. Определяется по формуле:
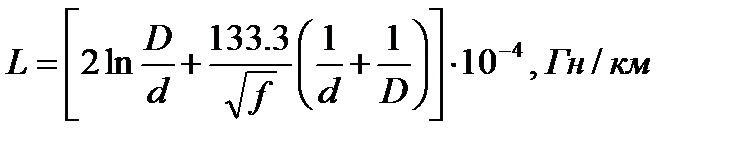
Первое слагаемое в квадратных скобах характеризует межпроводную индуктивность, которая не зависит от частоты, а зависит от соотношения диаметров.
Второе слагаемое в квадратных скобках характеризует внутреннюю индуктивность и зависит как от диаметров, так и от частоты.
Индуктивность цепи при f выше 1 МГц можно определять по упрощенной формуле:

Емкость коаксиальной цепи определяется по формуле емкости цилиндрического конденсатора:

где Еэ – эквивалентная относительная диэлектрическая проницаемость диэлектрика, между проводами.
Проводимость изоляции определяется по формуле
G = ω С tgδ,мкСм/км
Коаксиальные кабели практически используются в спектре от 60 км и выше, поэтому вторичные параметры определяются по упрощенным формулам (см. выше).






