Лекция № 38. Тема 1: Введение
1.1. Задачи, приводящие к дифференциальным уравнениям
Часто, рассматривая явления, мы не можем непосредственно установить вид исследуемой зависимости у от х. Однако мы можем установить зависимость между функцией, её производными и аргументом.
Рассмотрим следующие две задачи.
1. Задача о радиоактивном распаде. Экспериментально установлено, что скорость радиоактивного распада вещества массы М пропорциональна количеству нераспавшегося вещества, т.е.
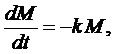
где k - коэффициент распада, который устанавливается экспериментально.
2. Задача о падении тела. С некоторой высоты падает тело массой т. Требуется установить по какому закону изменяется путь S, проходимый данным телом.
Согласно второму закону Ньютона имеем
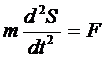 , где
, где 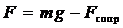 , а
, а 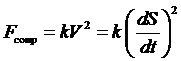 .
.
Таким образом, получим 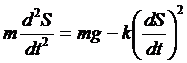 .
.
Полученные соотношения представляют собой дифференциальные уравнения для нахождения функций 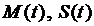 и являются математи-ческими моделями соответствующих физических процессов.
и являются математи-ческими моделями соответствующих физических процессов.
1.2. Определение дифференциального уравнения
Определение 1. Дифференциальным уравнением (ДУ) называется урав-нение, связывающее независимую переменную х, искомую функцию у (х) и её производные: 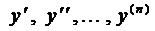 .
.
Его общий вид
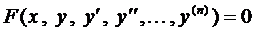 . (1)
. (1)
Дифференциальные уравнения, у которых функция у (х) является функцией одного переменного, называются обыкновенными ДУ.
Определение 2. Порядком ДУ называется порядок наивысшей производной, входящей в это уравнение.
Например, для первой задачи – уравнение первого порядка, для второй – уравнение второго порядка.
Определение 3. Решением ДУ (1) называется функция 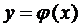 , которая при подстановке в уравнение обращает его в тождество.
, которая при подстановке в уравнение обращает его в тождество.
Процесс отыскания решения ДУ называется интегрированием ДУ.
Замечание 1. Наряду с термином “решение ДУ“ употребляется термин “интеграл ДУ“, под которым, как правило, понимается решение ДУ, полученное неявно, т.е. в виде 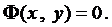
Например, для дифференциального уравнения 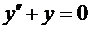 функцию
функцию 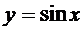 обычно называют решением, а для ДУ
обычно называют решением, а для ДУ 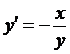 - выражение
- выражение 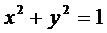 обычно называют интегралом уравнения.
обычно называют интегралом уравнения.
Тема 2: Дифференциальные уравнения первого порядка
2.1. Общие понятия. Теорема существования и единственности
Общий вид дифференциального уравнения первого порядка (ДУ-1)
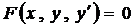 . (2)
. (2)
Если уравнение можно разрешить относительно производной, то
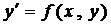 , (3)
, (3)
где функция 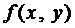 определена в некоторой области D.
определена в некоторой области D.
Для примера рассмотрим уравнение 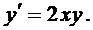 Нетрудно убедится в том, что его решением является функция
Нетрудно убедится в том, что его решением является функция 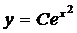 , где С - произвольная постоянная. И на любых других примерах можно убедится в том, что любое решение ДУ-1 есть бесконечное множество функций, которые определяются формулой, содержащей одну произвольную постоянную С, т.е. имеют вид
, где С - произвольная постоянная. И на любых других примерах можно убедится в том, что любое решение ДУ-1 есть бесконечное множество функций, которые определяются формулой, содержащей одну произвольную постоянную С, т.е. имеют вид
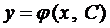 или
или 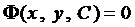 . (4)
. (4)
Определение 4. Общим решением или общим интегралом уравнения (2) или (3) называется функция (4) удовлетворяющая условиям:
1. Обращает в тождество уравнение при любых значениях С;
2. Для любой точки 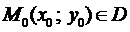 можно найти такое значение постоянной
можно найти такое значение постоянной 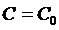 для которого
для которого 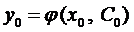 или
или 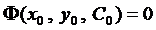 .
.
Давая произвольной постоянной С различные числовые значения, из общего решения получим так называемые частные решения.
Для того, чтобы из общего решения выделить конкретное частное решение, необходимо задать начальное условие, т.е. условие вида
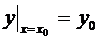 или
или 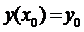 . (5)
. (5)
В этом случае задача о нахождении частного решения называется задачей Коши.
Пример 1. Решить задачу Коши: 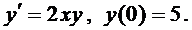
Как было показано, общее решение имеет вид 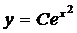 . Определим константу С, исходя из начального условия
. Определим константу С, исходя из начального условия
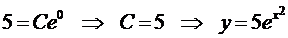 - решение задачи Коши.
- решение задачи Коши.
Теорема Коши. Если в дифференциальном уравнении 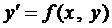 функция
функция 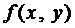 непрерывна в некоторой области D, содержащей точку
непрерывна в некоторой области D, содержащей точку 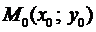 , то существует решение
, то существует решение 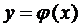 этого уравнения, удовлетво-ряющее начальному условию
этого уравнения, удовлетво-ряющее начальному условию 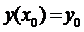 . Если, кроме этого, в этой области непрерывна производная
. Если, кроме этого, в этой области непрерывна производная 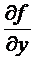 , то решение уравнения единственно.
, то решение уравнения единственно.
Пример 2. Найти область единственности решения ДУ
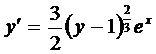 .
.
Здесь 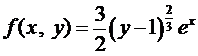 . Тогда
. Тогда
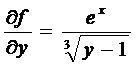
и при 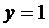 возможно нарушение единственности решения. Во всех остальных точках решение единственное.
возможно нарушение единственности решения. Во всех остальных точках решение единственное.
2.2. Уравнения с разделяющимися переменными
Рассмотрим ДУ-1 (3). Если 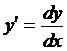 , то уравнение (3) можно пред-ставить в виде
, то уравнение (3) можно пред-ставить в виде
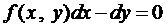 .
.
Если к тому же
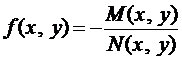 ,
,
то
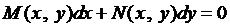 . (6)
. (6)
Пусть в уравнении (6) выполняются условия:
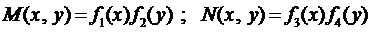 ,
,
тогда оно примет вид
 . (7)
. (7)
Определение 5. Уравнение (7) называется уравнением с разделяющи-мися переменными.
Разделим уравнение (7) на произведение 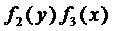 , тогда получим
, тогда получим
 (8)
(8)
Интегрируя уравнение (8), получим его общий интеграл
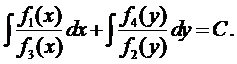 (9)
(9)
Замечание 2. Особого внимания требуют точки, где обращаются в нуль функции 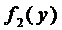 и
и 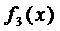 . Пусть, например,
. Пусть, например,  . Тогда уравнение (7) наряду с решением (9) имеет и решение
. Тогда уравнение (7) наряду с решением (9) имеет и решение 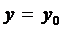 . Аналогично, если
. Аналогично, если 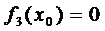 , то
, то 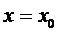 является решением уравнения (7).
является решением уравнения (7).
Пример 3. Найти общее решение уравнения 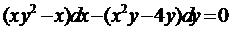 .
.
Преобразуем уравнение:
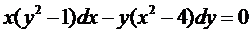
или
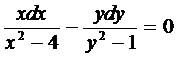 ,
,
при этом 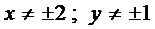 . Интегрируя уравнение, получим
. Интегрируя уравнение, получим
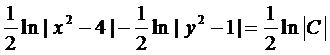
или
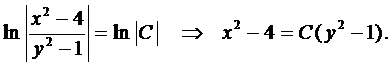
К этому решению нужно добавить решение вида 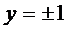 , а решение вида
, а решение вида 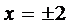 входит в общее решение при
входит в общее решение при 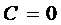 . Окончательно, имеем
. Окончательно, имеем
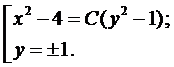
Пример 4. Решить задачу о радиоактивном распаде вещества:

Разделим переменные: 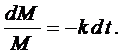
Интегрируя, получим
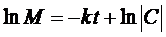 или
или  .
.
Если известна начальная масса M 0 при 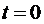 , тогда
, тогда
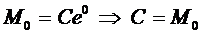 и
и 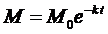 .
.
Определим коэффициент k из наблюдений. Пусть за время t 1 масса вещества стала равной M 1. Тогда
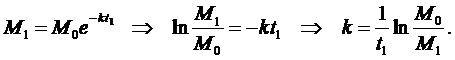
Таким образом, получили конкретный вид закона изменения заданной массы радиоактивного вещества в зависимости от времени.
Лекция № 39
2.3. Однородные уравнения
Определение 1. Функция 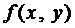 называется однородной функцией, если
называется однородной функцией, если 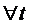 выполняется
выполняется 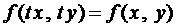 .
.
Например, функция 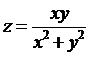 является однородной, так как
является однородной, так как
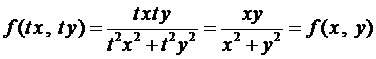 .
.
Определение 2. Уравнение вида 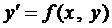 называется однородным уравнением, если
называется однородным уравнением, если 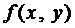 однородная функция.
однородная функция.
Покажем, что решение однородного уравнения сводится к решению уравнения с разделяющимися переменными.
По условию 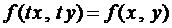 . Положим в этом тождестве
. Положим в этом тождестве 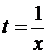 , тогда
, тогда
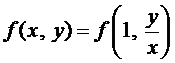
и уравнение примет вид
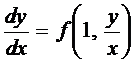 .
.
Сделаем замену 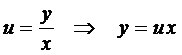 и
и 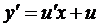 .
.
Тогда получим уравнение с разделяющимися переменными
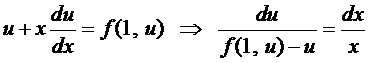
Интегрируя его, а затем, подставляя 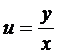 , находим решение.
, находим решение.
Замечание. Аналогично, как и для уравнений с разделяющимися переменными, если 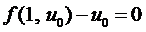 , то однородное уравнение обладает решением
, то однородное уравнение обладает решением 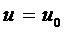 или
или 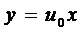 .
.
 Пример 1. Определить кривую, проходящую через точку
Пример 1. Определить кривую, проходящую через точку 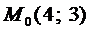 , если подкасательная АВ любой её точки есть среднее арифметическое координат.
, если подкасательная АВ любой её точки есть среднее арифметическое координат.
Если 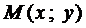 - текущая точка у
- текущая точка у
кривой, то по условию задачи,
получаем уравнение 
 у
у
Получили однородное урав- 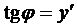
нение, поэтому сделаем замену О А В х
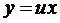 и
и 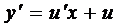 .
.
Тогда уравнение примет вид
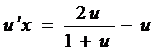 .
.
Разделяем переменные

и интегрируем
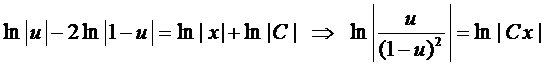 .
.
Выполнив обратную замену 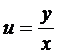 , имеем
, имеем
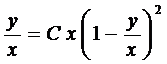 .
.
Окончательно, учитывая, что кривая проходит через заданную точку и подставляя в общее решение ее координаты
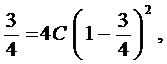
находим 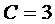 и получим искомое уравнение кривой
и получим искомое уравнение кривой
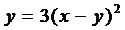 .
.
2.4. Линейные уравнения первого порядка (ЛУ–1)
Определение 3. Уравнение вида 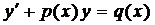 , где
, где  и
и 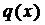 функции непрерывные на отрезке
функции непрерывные на отрезке 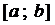 , называется линейным.
, называется линейным.
Его решение будем искать в виде
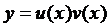 . (1)
. (1)
Продифференцируем выражение (1), а, затем подставим в ЛУ-1, получим
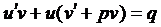 . (2)
. (2)
Функцию 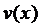 выберем из условия
выберем из условия
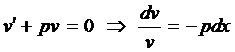 .
.
Проинтегрируем это уравнение
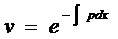 .
.
Тогда уравнение (2) примет вид
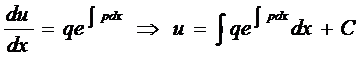 .
.
Окончательно, имеем
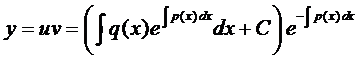 .
.
Пример 2. Найти общее решение уравнения 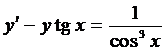 .
.
Решение ищем в виде 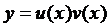 . Тогда для функции
. Тогда для функции 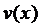 получаем уравнение
получаем уравнение

а для функции 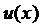 -
-
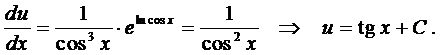
Окончательно, имеем
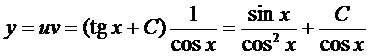 .
.
2.5. Уравнения Бернулли
Определение 4. Уравнение вида 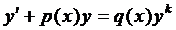 , где
, где 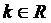 , называется уравнением Бернулли.
, называется уравнением Бернулли.
Отметим, что при 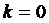 оно становится линейным, а при
оно становится линейным, а при 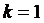 - уравнением с разделяющимися переменными. Поэтому в дальнейшем эти случаи не рассматриваем.
- уравнением с разделяющимися переменными. Поэтому в дальнейшем эти случаи не рассматриваем.
Покажем, что уравнение Бернулли путём замены 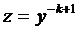 , приводится к линейному. Действительно,
, приводится к линейному. Действительно,
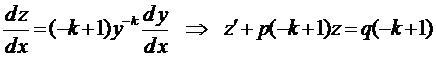 .
.
Таким образом, уравнения Бернулли интегрируются аналогично как линейные.
Пример 3. Найти общее решение уравнения 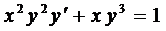 .
.
Разделим данное уравнение на 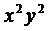 и получим уравнение Бернулли
и получим уравнение Бернулли
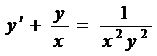 .
.
Здесь 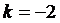 . Решение ищем в виде
. Решение ищем в виде 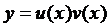 . Тогда
. Тогда
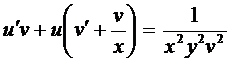 .
.
Для функции 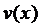 получаем уравнение
получаем уравнение
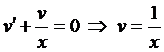 ,
,
а для функции 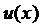 -
-
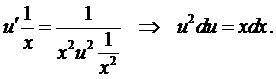
Проинтегрируем это уравнение, тогда 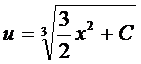 .
.
Таким образом, общее решение имеет вид
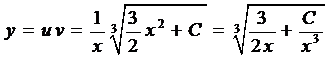 .
.
2.6. Уравнения в полных дифференциалах
Определение 5. Уравнение вида 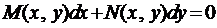 , называется уравнением в полных дифференциалах, если
, называется уравнением в полных дифференциалах, если
 , (3)
, (3)
где частные производные непрерывны в некоторой области.
Покажем, что равенство (3) является условием полного дифферен-циала.
Теорема. Если 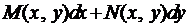 полный дифференциал некоторой функции
полный дифференциал некоторой функции 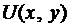 , то выполняется условие (3). Верно и обратное.
, то выполняется условие (3). Верно и обратное.
Пусть выражение 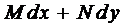 является полным дифференциалом. Это означает, что
является полным дифференциалом. Это означает, что 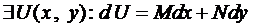 , так как
, так как
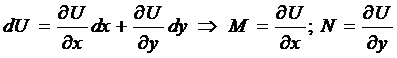 .
.
Продифференцировав первое полученное выражение по у, а второе по х, получим
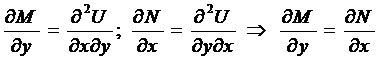 .
.
Обратно. Пусть выполняется условие (3). Требуется найти функцию 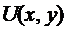 , которая должна удовлетворять условиям:
, которая должна удовлетворять условиям:
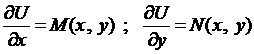 .
.
Интегрируя первое из них, получим
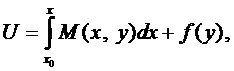
где 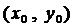 является фиксированной точкой из области определения функций
является фиксированной точкой из области определения функций 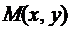 и
и 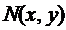 , а
, а  - произвольная функция. Теперь продифференцируем это выражение:
- произвольная функция. Теперь продифференцируем это выражение:
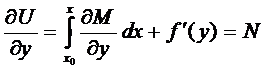
и воспользуемся условием (3)
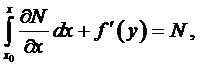
откуда
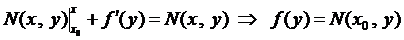 и
и 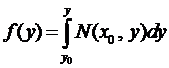 .
.
Таким образом, функция 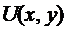 найдена
найдена
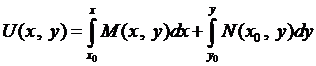 . (4)
. (4)
Теорема доказана. Возвращаемся к уравнению в полных дифферен-циалах. Если выполняется условие (3), то согласно теореме имеем
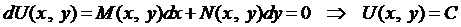 - общий интеграл.
- общий интеграл.
С учётом формулы (4) окончательно определяем общий интеграл уравнения в полных дифференциалах
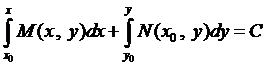 . (5)
. (5)
Пример 4. Решить задачу Коши
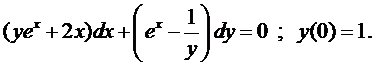
Проверим выполнение условия (3):
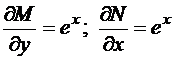 ,
,
т.е. имеем уравнение в полных дифференциалах. По формуле (5) получаем
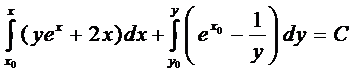
или
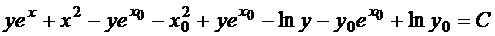 .
.
Приведём подобные члены и соберём все константы в одну:
 .
.
Значение константы С определим из начального условия:  .
.
Тогда решение задачи Коши будет иметь вид
 .
.
Лекция № 40. Тема 3: ДУ высших порядков
3.1. Определение ДУ п -го порядка
Общий вид дифференциального уравнения п -го порядка (ДУ- п):
 , (1)
, (1)
или разрешенного относительно старшей производной:
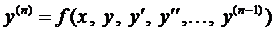 .
.
Для поиска частного решения необходимо задать начальные условия:
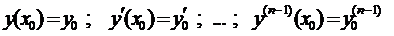 . (2)
. (2)
Определение 1. Общим решением или интегралом уравнения (1) назы-вается функция  или
или 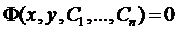 соответст-венно, которая:
соответст-венно, которая:
1. Удовлетворяет уравнению при любых значениях произвольных посто-янных 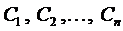 .
.
2. При любых заданных начальных условиях (2) из области определения можно найти такие 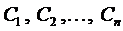 , что функция
, что функция  или
или 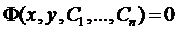 соответственно будет удовлетворять условиям (2).
соответственно будет удовлетворять условиям (2).
3.2. Уравнения, допускающие понижение порядка
3.2.1. 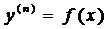 .
.
Для нахождения решения данного уравнения необходимо проинтегри-ровать его п раз.
Пример 1. Найти общее решение уравнения 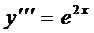 .
.
Проинтегрируем уравнение три раза:
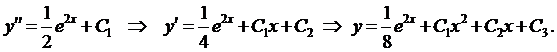
3.2.2. 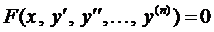 (нет у).
(нет у).
При помощи замены 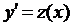 уравнение принимает вид
уравнение принимает вид
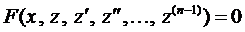 .
.
Пример 2. Найти общее решение уравнения 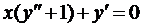 .
.
После замены 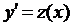 уравнение принимает вид
уравнение принимает вид
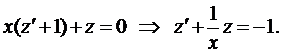
Это линейное уравнение, поэтому используем подстановку 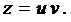
Тогда получим
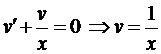
и
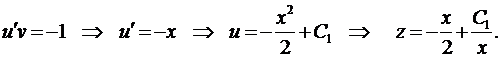
Так как 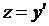 , то
, то
 .
.
Интегрируя, окончательно получаем
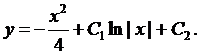
3.2.3. 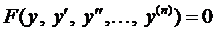 (нет х).
(нет х).
При помощи замены 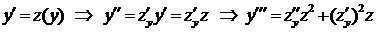 …
…
уравнение принимает вид
 .
.
Пример 3. Решить задачу Коши 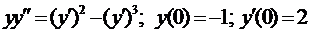 .
.
После замены 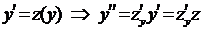 получим уравнение с разде-ляющимися переменными:
получим уравнение с разде-ляющимися переменными:
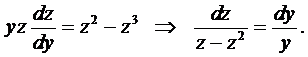
Проинтегрируем:
 .
.
Воспользуемся начальными условиями
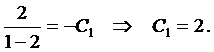
Разрешим уравнение относительно  и разделим переменные
и разделим переменные
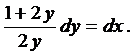
Проинтегрируем
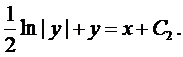
Из начальных условий находим 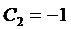 и, окончательно, получаем частное решение
и, окончательно, получаем частное решение
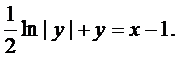
Тема 4: Линейные дифференциальные уравнения второго порядка
4.1. Линейные однородные дифференциальные уравнения второго порядка (ЛОДУ-2). Определитель Вронского и его свойства
Общий вид
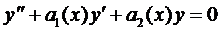 , (3)
, (3)
где 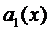 и
и 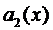 непрерывные на некотором отрезке
непрерывные на некотором отрезке 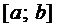 функции.
функции.
Определение 2. Функции 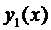 и
и 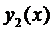 называются линейно зависи-мыми (ЛЗ) на
называются линейно зависи-мыми (ЛЗ) на 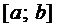 , если
, если 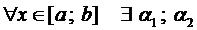 , где, по крайней мере, одно из них отличное от нуля, и для которых выполняется равенство
, где, по крайней мере, одно из них отличное от нуля, и для которых выполняется равенство 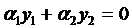 или, если
или, если 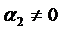 , то
, то 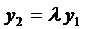 , т.е.
, т.е. 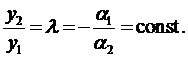
В противном случае, функции 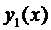 и
и 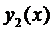 называются линейно независимыми (ЛНЗ).
называются линейно независимыми (ЛНЗ).
Например, функции 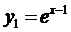 и
и 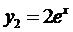 - ЛЗ, так как
- ЛЗ, так как 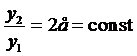 , а функции
, а функции  и
и 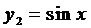 - ЛНЗ, так как
- ЛНЗ, так как 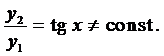
Для выяснения ЛЗ или ЛНЗ решений уравнения (3) используется определитель Вронского
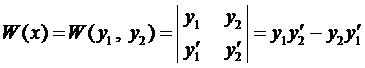 ,
,
что следует из теорем:
Теорема 1. Если функции 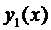 и
и 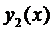 линейно зависимы (ЛЗ) на
линейно зависимы (ЛЗ) на 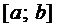 , то определитель Вронского
, то определитель Вронского 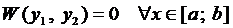 .
.
Так как 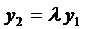 , то
, то
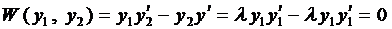 .
.
Теорема 2. Если определитель Вронского, составленный из решений уравнения (3), при некотором 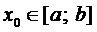 отличен от нуля, т.е.
отличен от нуля, т.е. 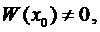 то
то 
Так как 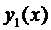 и
и 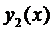 решения уравнения (3), то
решения уравнения (3), то
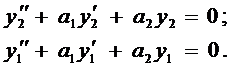
Первое равенство умножим на 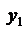 , второе на
, второе на 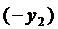 и сложим полученные результаты. С учётом, что
и сложим полученные результаты. С учётом, что
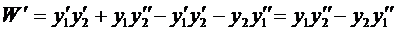 ,
,
получим уравнение с разделяющимися переменными
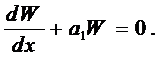
Найдём его решение, удовлетворяющее начальному условию 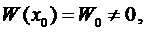
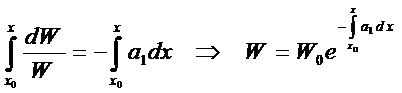 (4)
(4)
или
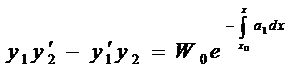 .
.
Формула (4) называется формулой Лиувилля. Из неё видно, что если
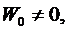 то
то 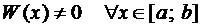 .
.
Замечание 1. Из формулы (4) также следует, что если при некотором. 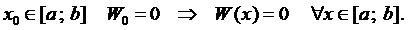
Замечание 2. По формуле Лиувилля, зная одно из решений ЛОДУ-2, можно найти другое. Разделив обе части равенства (4) на 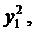 получим
получим
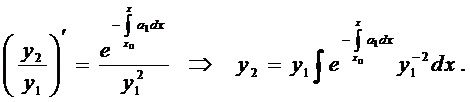
Теорема 3. Если решения ЛОДУ-2 (3) ЛНЗ на 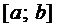 , то
, то 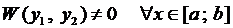 .
.
Предположим обратное, т.е. 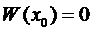 при некотором
при некотором 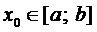 . Тогда по теореме 2
. Тогда по теореме 2 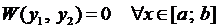 . Предположим, что
. Предположим, что 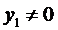 (в противном случае определитель Вронского тождественно равен нулю), тогда имеем равенство
(в противном случае определитель Вронского тождественно равен нулю), тогда имеем равенство
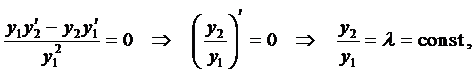
т.е. функции 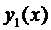 и
и 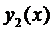 линейно зависимы. Полученное противоречие доказывает теорему.
линейно зависимы. Полученное противоречие доказывает теорему.
4.2. Теорема о структуре общего решения ЛОДУ-2
Теорема 4. Если функции 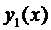 и
и 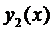 - два ЛНЗ решения уравне-ния (3), то его общее решение имеет вид
- два ЛНЗ решения уравне-ния (3), то его общее решение имеет вид 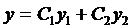 , где
, где 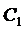 и
и 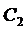 произвольные константы.
произвольные константы.
Вначале покажем, что 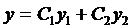 является решением уравнения (3), для чего подставим его в (3) и сгруппируем члены при
является решением уравнения (3), для чего подставим его в (3) и сгруппируем члены при 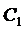 и
и 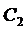 :
:
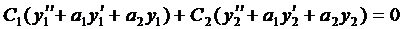 .
.
Далее покажем, что для любых начальных условий вида 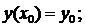
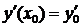 можно найти значения
можно найти значения 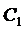 и
и 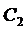 , при которых такое решение удовлетворяло бы им.
, при которых такое решение удовлетворяло бы им.
Подставим в эти условия 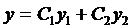 , тогда получим систему для определения значений
, тогда получим систему для определения значений 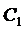 и
и 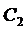
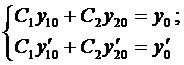 (5)
(5)
с определителем Вронского
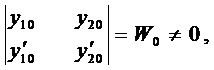
так как 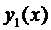 и
и 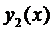 - ЛНЗ решения уравнения (3).
- ЛНЗ решения уравнения (3).
Из решения системы (5) определяем 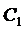 и
и 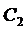 . Таким образом,
. Таким образом,
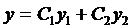
является общим решением уравнения (3).
Лекция № 41
4.3. ЛОДУ-2 с постоянными коэффициентами
Общий вид ЛОДУ-2
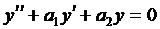 , (1)
, (1)
где 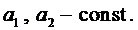
Будем искать решение этого уравнения в виде 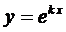 .
.
Подставим в уравнение (1):
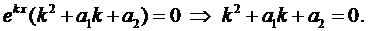 (2)
(2)
Уравнение (2) называется характеристическим уравнением.
В зависимости от значений корней характеристического уравнения возможны следующие три случая:






