а уравнение касательной плоскости –
или 
.
Тема 3*: Векторная функция скалярного аргумента
3.1. Векторная функция. Предел. Непрерывность
Аналогично, как и для плоской линии, пространственная линия может быть задана параметрическими уравнениями вида
Например, 
– уравнения прямой в пространстве, а 
, где 
- уравнения винтовой линии (спираль).
Замечание 2. В механике под параметром t подразумевается время.
Рассмотрим радиус-вектор 
, координаты которого являются функциями параметра t
. (1)
Каждому значению параметра t по формуле (1) соответствует определённый вектор 
, т.е. является функцией скалярного аргумента t. Таким образом, векторная функция скалярного аргумента записывается в виде 
. z
Определение. Линия, описанная годограф
концом вектора 
, называется
годографом векторной функции
. 
Предел и непрерывность векторной 
y
функции определяется через скалярные х
функции 
.
Если существуют пределы:
то 
, где 
.
Аналогично определяется непрерывность векторной функции через непрерывность функций .
3.2. Производная векторной функции
Дадим приращение аргументу t. В результате векторная функция получит приращение
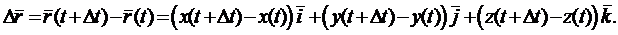
Рассмотрим отношение 
. Если функции являются дифференцируемыми, то
. (2)
Формула (2) определяет производную векторной функции скалярного аргумента. Модуль этого вектора равен
.
Выясним геометрический смысл производной.
М 
М 1
О 
Из рисунка видно, что при 
, т.е. производная имеет направление касательной. Нормалей к пространственной кривой в данной точке можно провести бесконечное множество – все они лежат в плоскости, которая называется нормальной плоскостью. Исходя из геометрического смысла производной, получаем уравнение касательной
и уравнение нормальной плоскости
.
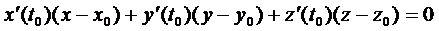Замечание 3. Из определения производной следует, что правила её нахождения такие же, как и для скалярной функции одного переменного.
Аналогично, как и для плоской линии, вводится понятие её кривизны.
Формула для вычисления кривизны пространственной линии имеет вид
.
Пример 2. Показать, что если 
то 
Действительно, так как 
то, дифференцируя, получаем 
, что и требовалось доказать.
Пример 3. Составить уравнение касательной, нормальной плоскости и вычислить кривизну винтовой линии в точке 
.
Вычислим значения функций и их производных в соответствующей точке:
Составим уравнение касательной
и нормальной плоскости
Для вычисления кривизны найдём векторное произведение векторов 
и 
Тогда
.
Лекция № 36. Тема 4: Экстремум функции нескольких переменных
4.1. Необходимые условия экстремума
Определение 1. Функция 
имеет максимум (минимум) в точке 
, если для любой точки 
выполняется неравенство 
. Максимум и минимум называются экстремумами функции.
Возьмем точку , дадим в ее окрестности приращения аргументам 
, тогда приращение функции
и, если 
, то точка - точка максимума, если 
- точка минимума. z
Пример 1. Рассмотрим функцию
и точку 
(см. рис.).
В этой точке имеем
- точка минимума. O y
x
Теорема (необходимые условия экстремума). Если функция достигает экстремума в точке , то в этой точке частные производные 
и 
равны нулю, или не существуют.
Дадим переменной у определённое значение у 0. Тогда 
будет функцией одного переменного х. При значении 
она имеет экстремум, поэтому частная производная 
, либо не существует.
Аналогично доказывается и для частной производной .
Это условие не является достаточным, что видно из примера.
Пример 2. Рассмотрим функцию 
.
Тогда
В этой точке полное приращение функции 
, откуда следует, что в её окрестности 
принимает как положительные, так и отрицательные значения. Экстремума нет.
Определение 2. Точки, в которых частные производные равны нулю либо не существуют, называются критическими. Точки, в которых частные производные равны нулю, называются стационарными.
Замечание. Из определения градиента следует, что в стационарных точках градиент является нулевым вектором.
4.2. Достаточные условия экстремума
Теорема. Если в некоторой окрестности стационарной точки функция имеет непрерывные частные производные до третьего порядка включительно, то если:
1. 
- экстремум есть, при этом, если 
, а при 
.
2. 
- экстремума нет.
3. 
- ответа нет, требуются дополнительные исследования.
Здесь 
; 
; 
.
Пример 3. Исследовать на экстремум функцию 
.
Из данной системы, получаем 
,
т.е. найдены две стационарные точки: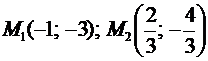 
.
В точке 
, 
.
В точке 
экстремума нет.
Пример 4*. Канава для стока воды имеет в сечении равнобочную трапецию площадью S. Требуется определить размеры канавы, при которых были бы минимальные потери жидкости.
h
a
a
Если потери обозначить через Q, то они пропорциональны смоченному периметру сечения, т.е.
, где 
.
Три переменные 
связаны зависимостью
.
Таким образом, мы определили функцию
,
которую необходимо исследовать на экстремум. Имеем
;
;
.
Используя достаточные условия экстремума, можно показать, что эти значения определяют точку минимума.
4.3. Нахождение наибольшего и наименьшего значений функции
в замкнутой области
Для нахождения наибольшего и наименьшего значений поступают, как и для случая функции одной переменной, а именно:
1. Определяют значения функции в критических точках, принадлежащих области;
2. Определяют наибольшие и наименьшие значения функции на границе области;
3. Из полученных значений выбирают наибольшее и наименьшее.
Пример 5. Найти наибольшее и наименьшее значения функции 
в области D: 
у
А
3
-1 О 1 3 х
С В
Область D - это треугольник АВС.
Определяем критические точки, принадлежащие области D
На границе 
.
.
Вычисляем значения функции на концах отрезка АВ
.
На границе 
.
.
Вычисляем значения функции на концах отрезка АС
.
На границе 
.
т.е. получили точку B.
Из полученных значений выбираем наибольшее и наименьшее:
Лекция № 37
4.4. Условный экстремум
Определение 1. Условным экстремумом функции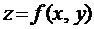 
называ-ется экстремум, достигнутый при условии, что переменные х, у связаны уравнением 
Геометрически задача состоит в том, чтобы на этой линии найти такую точку М 0, в которой значение функции 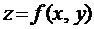было наибольшим (наименьшим) по сравнению с другими значениями на этой линии в некоторой окрестности точки М 0. Такие точки называются точками условного (относительного) экстремума.
Рассмотрим геометрический смысл этого понятия на примере.
Пример 1. Графиком функции 
является верхняя полу-сфера. Рассмотрим прямую линию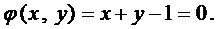 
z
O y
M 0
x
Для точек этой прямой, в силу симметрии, функция достигает макси-мального значения в точке 
. Это и есть точка условного макси-мума на линии.
Теперь сформулируем задачу, которую предстоит решить. Требуется найти точки условного экстремума функции 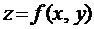при условии 
которое называется уравнением связи.
По правилу нахождения полной производной от функции 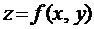, получим
(1)
В точках экстремума формула (1) принимает вид
(2)
Аналогично поступаем с уравнением связи
. (3)
Умножим выражение (3) на неопределённый множитель 
, сложим с выражением (2) и проведём группировку членов
. (4)
Подберём множитель так, чтобы в выражении (4) выполнялось
.
Тогда получим, что в точках экстремума удовлетворяются три уравнения:
(5)
Из системы (5) определяются х, у и множитель .
Условиям (5) можно придать другую форму, если ввести так назы-ваемую функцию Лагранжа
,
тогда система (5) примет вид
(6)
Рассмотренный приём называется методом множителей Лагранжа. Системы (5) или (6) представляют собой необходимые условия условного экстремума.
Достаточные условия существования условного экстремума опреде-ляются по знаку определителя
. (7)
Если в точке 
, то в этой точке условный максимум.
Если в точке 
, то - условный минимум.
Если 
- ответа нет, требуются дополнительные исследования.
Метод множителей Лагранжа легко распространить для случая функции п переменных с т связями.
Пусть требуется найти условный экстремум функции 
при условиях
Для этого составляется функция Лагранжа
и приравниваются к нулю её частные производные
. (8)
Из системы (8) определяются 
и вспомогательные мно-жители 
.
Пример 2. Найти условный экстремум функции 
, если уравнение связи 
.
Составим функцию Лагранжа
.
Получим систему
Легко получить решение данной системы: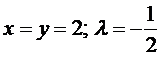 
.
Получили точку 
. Воспользуемся достаточными условиями экстремума. Вычислим в этой точке определитель (7)
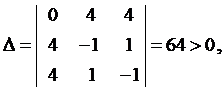
т.е. М 0 - точка условного максимума, 
.
4.5. Метод наименьших квадратов
Пусть в результате опыта установлено, что значениям величины х равным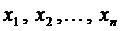 
соответствуют значения величины у: 
. Требуется установить вид функции 
, которая наилучшим образом описала бы полученную из опыта зависимость.
В функциональную зависимость общего вида, которая определяется из сути опыта, включим параметры: а, b, с, …, которые подберём таким образом, чтобы сумма квадратов разностей значений экспериментально полученных и вычисленных по формуле 
была наимень-шей, т.е.
Необходимые условия:
дают систему для определения параметров а, b, с, ….
Рассмотрим случай, когда аппроксимация (приближение) эксперимен-тальных данных осуществляется линейной зависимостью 
.
Тогда
и
