Вначале покажем, что если 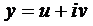 является решением уравнения (1), то этому уравнению удовлетворяют функции u и v. Подставим
является решением уравнения (1), то этому уравнению удовлетворяют функции u и v. Подставим 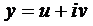 в уравнение (1) и выделим действительную и мнимую части:
в уравнение (1) и выделим действительную и мнимую части:
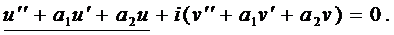
Подчеркнутый член и выражение в скобках равны нулю.
Итак, в этом случае частные решения имеют вид
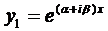 и
и 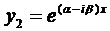 .
.
Если воспользоваться формулой Эйлера, которая будет доказана позже,
 ,
,
то
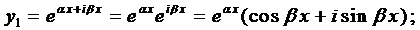
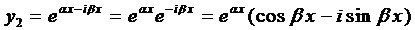
и, как показано выше, решениями уравнения (1) будут являться функции:
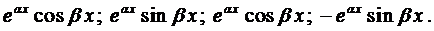
Очевидно, линейно-независимыми среди них будут
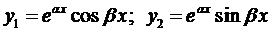 ,
,
Так как 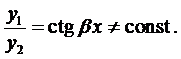
Окончательно, общее решение будет иметь вид
 . (5)
. (5)
Пример 3. Найти общее решение уравнения 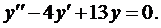 .
.
Составим характеристическое уравнение:
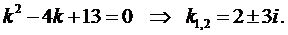
Воспользуемся формулой (5):
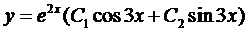 .
.
4.4. Линейные неоднородные дифференциальные уравнения второго порядка
Общий вид линейного неоднородного дифференциального уравнения второго порядка (ЛНДУ-2)
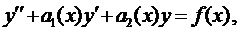 (6)
(6)
где функции 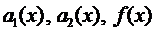 непрерывны на некотором отрезке
непрерывны на некотором отрезке 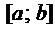 .
.
Ему соответствует однородное уравнение
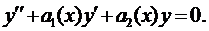 (7)
(7)
Пусть известно общее решение уравнения (7)
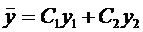 . (8)
. (8)
Теорема (о структуре общего решения ЛНДУ-2). Общее решение ЛНДУ-2 является суммой частного решения 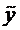 уравнения (6) и общего решения
уравнения (6) и общего решения 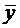 соответствующего однородного (7).
соответствующего однородного (7).
Вначале покажем, что 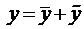 является решением уравнения (6), для чего подставим его в уравнение (6) и сгруппируем члены
является решением уравнения (6), для чего подставим его в уравнение (6) и сгруппируем члены
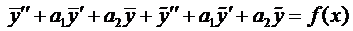 .
.
Сумма первых трёх членов левой части равенства равна нулю, так как 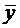 - общее решение однородного уравнения, а сумма остальных трёх членов равна
- общее решение однородного уравнения, а сумма остальных трёх членов равна 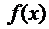 , так как
, так как 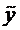 - есть частное решение уравнения (6).
- есть частное решение уравнения (6).
Таким образом, 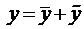 является решением уравнения (6).
является решением уравнения (6).
Теперь покажем, что для любых начальных условий вида 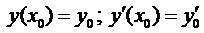 можно найти значения
можно найти значения  и
и 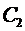 , при которых решение удовлетворяло бы им. Подставим решение
, при которых решение удовлетворяло бы им. Подставим решение
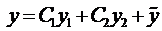
в эти условия, тогда получим систему
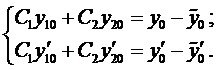 (9)
(9)
Система (9) является линейной системой для определения 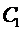 и
и 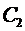 с определителем
с определителем
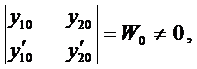
так как  и
и  - ЛНЗ решения уравнения (7). Из решения системы (9) определяем
- ЛНЗ решения уравнения (7). Из решения системы (9) определяем 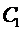 и
и 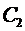 . Таким образом,
. Таким образом, 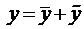 является общим решением уравнения (6).
является общим решением уравнения (6).
Замечание. Если 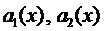 - функции от х, то не существует общих методов интегрирования уравнений (6) и (7). Рассмотрим случай, когда известно общее решение соответствующего однородного уравнения.
- функции от х, то не существует общих методов интегрирования уравнений (6) и (7). Рассмотрим случай, когда известно общее решение соответствующего однородного уравнения.
4.5. Метод вариации произвольных постоянных (метод Лагранжа)
Пусть нам известно общее решение уравнения (7), т.е. 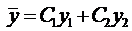 . Тогда решение уравнения (6) будем искать в виде
. Тогда решение уравнения (6) будем искать в виде
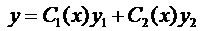 .
.
Продифференцируем это равенство:
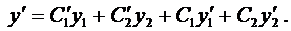
В силу произвольности выбора функций 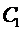 и
и 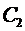 положим
положим
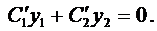 (10)
(10)
Тогда
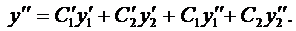
Подставляя 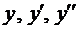 в уравнение (6) и группируя члены, получаем
в уравнение (6) и группируя члены, получаем
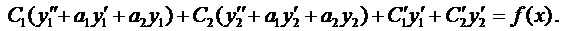 (11)
(11)
Выражения в скобках в формуле (11) равны нулю, объединяя полученные результаты, приходим к системе
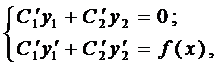 (12)
(12)
из которой единственным образом находятся 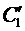 и
и 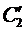 , так как её опре-делитель является определителем Вронского
, так как её опре-делитель является определителем Вронского 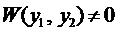 . И тогда
. И тогда
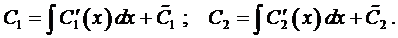
Пример 4. Методом вариации произвольных постоянных найти общее решение уравнения 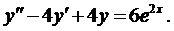
Найдём общее решение соответствующего однородного уравнения
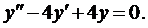
Составим характеристическое уравнение
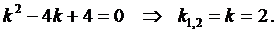
Воспользуемся формулой (4) 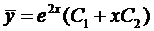 .
.
Здесь 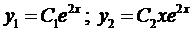 .
.
Составим систему (12)
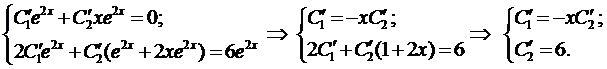
Интегрируя последнее уравнение системы, находим 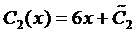 , а из первого уравнения определяем
, а из первого уравнения определяем 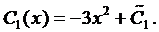
Окончательно получим общее решение
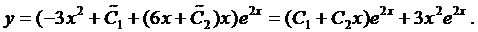
Лекция № 42
4.6. ЛНДУ-2 с постоянными коэффициентами со специальной правой частью
Общий вид линейного неоднородного дифференциального уравнения
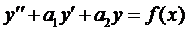 , (1)
, (1)
где 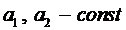 .
.
Как известно, общее решение уравнения (1) имеет вид 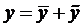 . Рассмотрим, как можно определить частное решение
. Рассмотрим, как можно определить частное решение  в зависимости от вида правой части (1) в некоторых случаях:
в зависимости от вида правой части (1) в некоторых случаях:
1. 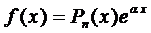 , где
, где 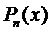 - многочлен п -ой степени.
- многочлен п -ой степени.
Зададим вид частного решения в форме 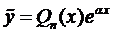 , где
, где
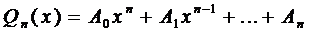
многочлен п -ой степени с неопределёнными коэффициентами. Найдём его производные:
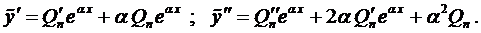
Подставим эти выражения в уравнение (1) и сократим на 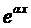
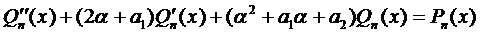 . (2)
. (2)
Здесь возможны случаи:
1.1. Число  не является корнем характеристического уравнения, т.е.
не является корнем характеристического уравнения, т.е. 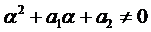 . Тогда слева и справа в выражении (2) стоят многочлены п -ой степени и, приравнивая коэффициенты при одинаковых степенях, находим неопределённые коэффициенты
. Тогда слева и справа в выражении (2) стоят многочлены п -ой степени и, приравнивая коэффициенты при одинаковых степенях, находим неопределённые коэффициенты 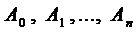 .
.
1.2. Число  является простым корнем характеристического уравнения, т.е.
является простым корнем характеристического уравнения, т.е. 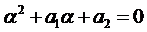 , а из теоремы Виета следует
, а из теоремы Виета следует 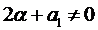 . Тогда слева в выражении (2) стоит многочлен (п - 1)-ой степени, а справа п -ой степени. Поэтому, для того чтобы коэффициенты
. Тогда слева в выражении (2) стоит многочлен (п - 1)-ой степени, а справа п -ой степени. Поэтому, для того чтобы коэффициенты 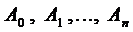 были определены, необходимо частное решение искать в виде многочлена (п + 1)-ой степени, но без свободного члена, так как он исчезает при дифференцировании, т.е.
были определены, необходимо частное решение искать в виде многочлена (п + 1)-ой степени, но без свободного члена, так как он исчезает при дифференцировании, т.е. 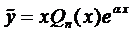 .
.
1.3. Число  является двукратным корнем характеристического уравнения, т.е.
является двукратным корнем характеристического уравнения, т.е. 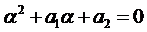 , а из теоремы Виета следует
, а из теоремы Виета следует 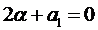 . Тогда слева в выражении (2) стоит многочлен (п - 2)-ой степени, а справа - (п - 1)-ой степени. Рассуждая аналогично, получаем
. Тогда слева в выражении (2) стоит многочлен (п - 2)-ой степени, а справа - (п - 1)-ой степени. Рассуждая аналогично, получаем 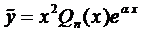 .
.
Рассмотренные три случая можно объединить общим правилом
Правило 1. Если правая часть уравнения (1) имеет вид 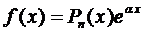 , то частное решение следует искать в виде
, то частное решение следует искать в виде 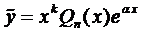 , где
, где 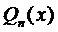 - многочлен п -ой степени с неопределёнными коэффициентами, а
- многочлен п -ой степени с неопределёнными коэффициентами, а 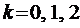 - кратность корня
- кратность корня  характеристического уравнения.
характеристического уравнения.
Пример 1. Найти общее решение уравнения 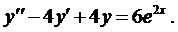
На предыдущей лекции было найдено общее решение соответствующего однородного уравнения
 .
.
Частное решение будем искать в виде 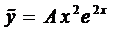 (случай 1.3).
(случай 1.3).
Подставим это выражение в наше уравнение и сократим на 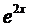 :
:
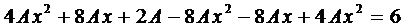
или
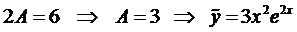 .
.
Тогда общее решение будет иметь вид
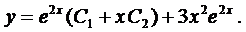
2. 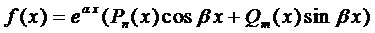 , где
, где 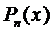 и
и 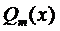 - многочлены п -ой и т -ой степени соответственно.
- многочлены п -ой и т -ой степени соответственно.
Частное решение будем искать в виде
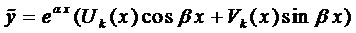 ,
,
где 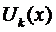 и
и 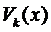 многочлены с неопределёнными коэффициентами, а
многочлены с неопределёнными коэффициентами, а 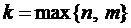 .
.
Найдём производные:
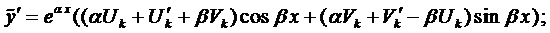
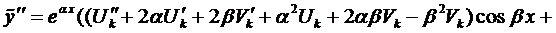
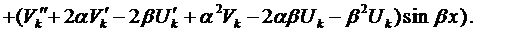
Если подставить эти выражения в уравнение (1), сократить на 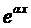 и приравнять коэффициенты при
и приравнять коэффициенты при 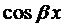 и
и 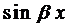 , то получим систему
, то получим систему
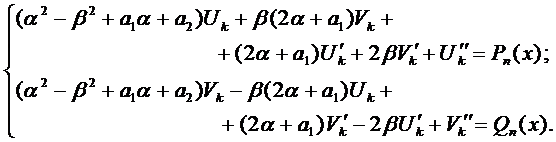 (3)
(3)
Если подставить числа 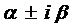 в характеристическое уравнение уравнения (1), то получим
в характеристическое уравнение уравнения (1), то получим 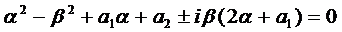 и тогда возможны случаи:
и тогда возможны случаи:
2.1. Числа 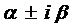 не являются корнями характеристического уравнения, т.е.
не являются корнями характеристического уравнения, т.е.
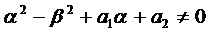 .
.
Тогда слева в уравнениях (3) стоят многочлены степени 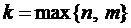 . Поэтому можно приравнять коэффициенты при одинаковых степенях х. В результате получим систему для определения коэффициентов многочленов
. Поэтому можно приравнять коэффициенты при одинаковых степенях х. В результате получим систему для определения коэффициентов многочленов 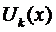 и
и 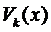 .
.
2.2. Числа 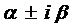 - корни характеристического уравнения, т.е.
- корни характеристического уравнения, т.е.
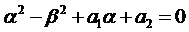 и
и 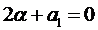 .
.
Тогда слева в уравнениях (3) стоят многочлены степени на единицу меньшую, чем k и, рассуждая аналогично, как и ранее, частное решение ищем в виде
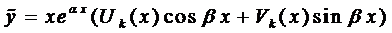 .
.
Итак, получаем
Правило 2. Если правая часть уравнения (1) имеет вид
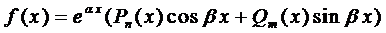 ,
,
то частное решение следует искать в виде
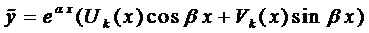 ,
,
если 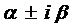 не являются корнями характеристического уравнения, и в виде
не являются корнями характеристического уравнения, и в виде
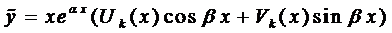 ,
,
если 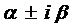 - корни характеристического уравнения, где
- корни характеристического уравнения, где 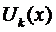 и
и 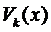 многочлены с неопределёнными коэффициентами, а
многочлены с неопределёнными коэффициентами, а 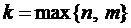 .
.
Замечание 1. Правило 2 справедливо и для случая 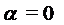 . Тогда
. Тогда
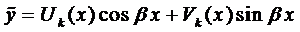
и, если 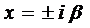 корень характеристического уравнения, то
корень характеристического уравнения, то
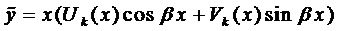
Замечание 2. Если правая часть уравнения (1) представляет собой сумму двух функций, относящихся к правилам 1-2, то частное решение в силу линейности уравнения ищется в виде суммы двух функций, которые определяются соответственно правилами 1-2.
Пример 2. Найти частное решение уравнения
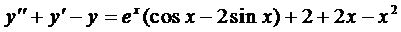 .
.
Здесь правая часть уравнения представляется в виде суммы двух функций:
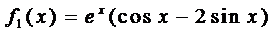 и
и 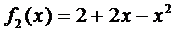 .
.
Поэтому решение ищем в виде 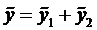 , где
, где 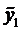 является частным решением уравнением
является частным решением уравнением
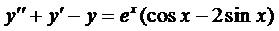 . (4)
. (4)
а 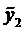 является частным решением уравнения
является частным решением уравнения
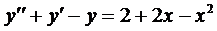 . (5)
. (5)
Для этого случая решение имеет вид (случай 2.1)
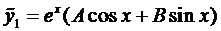 .
.
Подставим это выражение в уравнение (4):
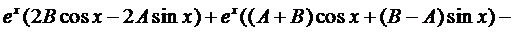
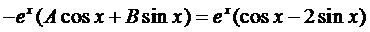 .
.
Сократим на 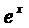 и приравняем коэффициенты при
и приравняем коэффициенты при 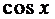 и
и 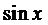 :
:
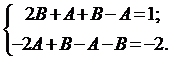
Из решения системы получаем
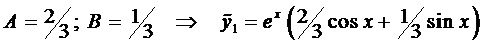 .
.
Решение уравнения (5) ищем в виде (случай 1.1)
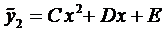 .
.
Подставим это выражение в уравнение (5)
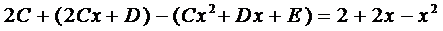 .
.
Приравнивая коэффициенты при 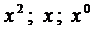 , приходим к системе
, приходим к системе
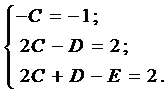
Из решения системы последовательно находим
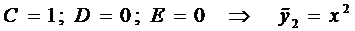 .
.
Окончательно получим
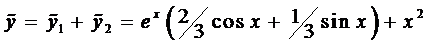 .
.
Лекция № 43. Тема 5: Линейные ДУ высших порядков
5.1. Линейные дифференциальные уравнения п -го порядка
Общий вид линейного дифференциального уравнения п -го порядка (ЛДУ - п)
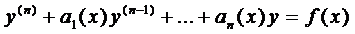 . (1)
. (1)
Ему соответствует однородное уравнение п -го порядка
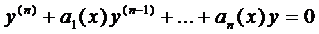 (2)
(2)
Определение 1. Функции 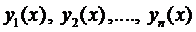 называются линейно зависимыми (ЛЗ) на
называются линейно зависимыми (ЛЗ) на 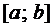 , если
, если 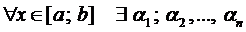 , где, по крайней мере, одно из них отлично от нуля, для которых выполняется
, где, по крайней мере, одно из них отлично от нуля, для которых выполняется 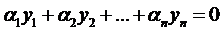 . В противном случае функции называются линейно независимыми (ЛНЗ).
. В противном случае функции называются линейно независимыми (ЛНЗ).
Для выяснения ЛЗ или ЛНЗ решений уравнения (2) также используется определитель Вронского, который для данного случая имеет вид
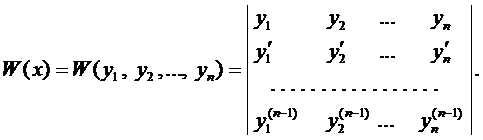
При этом, если 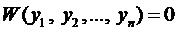 , то система функций ЛЗ. Если же для п частных решений
, то система функций ЛЗ. Если же для п частных решений 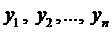 уравнения (2)
уравнения (2) 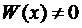 , то эти решения являются ЛНЗ.
, то эти решения являются ЛНЗ.
Справедливы также теоремы о структуре решений уравнений (1-2):
Теорема 1. Если 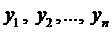 - ЛНЗ решения уравнения (2), то его общее решение имеет вид
- ЛНЗ решения уравнения (2), то его общее решение имеет вид
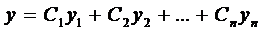 ,
,
где 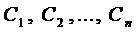 произвольные константы.
произвольные константы.
Теорема 2. Общее решение ЛНДУ - п есть сумма частного решения  уравнения (1) и общего решения
уравнения (1) и общего решения 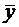 соответствующего однородного (2), т.е.
соответствующего однородного (2), т.е. 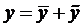 .
.
Доказательства этих теорем аналогичны, как и для случая ЛДУ – 2.
Если известно общее решение соответствующего однородного уравнения (2), то общее решение уравнения (1) можно находить методом вариации произвольных постоянных. Тогда система для нахождения функций 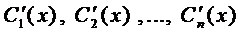 имеет вид
имеет вид
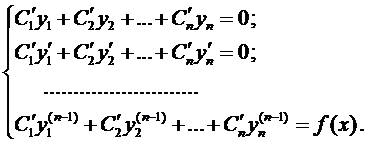
Остановимся на случае, когда все коэффициенты 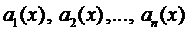 в уравнениях (1-2) являются константами. Тогда для однородного уравнения имеем характеристическое уравнение
в уравнениях (1-2) являются константами. Тогда для однородного уравнения имеем характеристическое уравнение
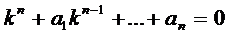 . (3)
. (3)
По характеру корней уравнения (3) определяются частные ЛНЗ решения:
Правило. Каждому действительному корню k характеристического уравнения (3) т -ой кратности соответствует т ЛНЗ решений вида
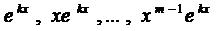 .
.
Каждой паре комплексных корней 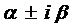 кратности т соответствует 2 т ЛНЗ решений вида
кратности т соответствует 2 т ЛНЗ решений вида
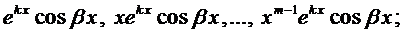
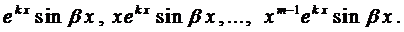
Для случая уравнения со специальной правой частью  исполь-зуется аналогичное правило, как и для ЛНДУ-2, для нахождения вида частного решения
исполь-зуется аналогичное правило, как и для ЛНДУ-2, для нахождения вида частного решения  .
.
Пример 1. Найти общее решение ДУ
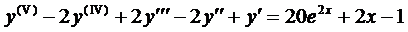 .
.
Ему соответствует однородное уравнение
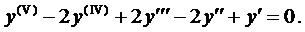
Составим характеристическое уравнение
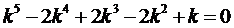 .
.
Найдём его корни
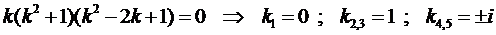 .
.
Тогда, согласно правилу, получаем общее решение однородного уравнения
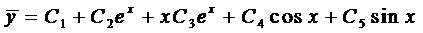 .
.
Частное решение неоднородного уравнения будем искать в виде 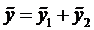 , где
, где 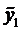 частное решение уравнения
частное решение уравнения
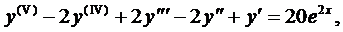 (4)
(4)
а 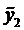 частное решение уравнения
частное решение уравнения
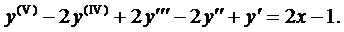 (5)
(5)
Так как число 2 не является корнем характеристического уравнения, то 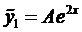 . Подставим это выражение в уравнение (4), предварительно сократив его на
. Подставим это выражение в уравнение (4), предварительно сократив его на 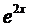 :
:
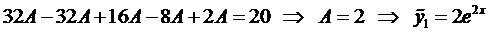 .
.
Частное решение уравнения (5) ищем в виде
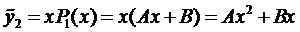 ,
,
так как нуль является корнем характеристического уравнения.
Подставим это выражение в уравнение (5):
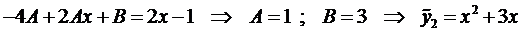 .
.
Таким образом, получаем общее решение данного уравнения
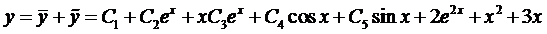 .
.
5.2*. Понятие о краевой задаче
При решении некоторых задач требуется проинтегрировать ДУ не при начальных условиях (задача Коши), а с учётом значений искомой функции или её производных в некоторых точках. Условия, налагаемые на значения функции, её производных на концах отрезка, называются краевыми условиями, а соответствующая задача – краевой задачей.
При этом для корректности решаемой задачи число таких условий должно быть равно числу констант в общем решении. Такие задачи рассматриваются в курсе сопротивления материалов, а ещё более общие задачи встречаются в курсе уравнений математической физики.
Рассмотрим в качестве примера задачу изгиба балки на упругом основании.
 y
y
q (x)
- l O l x
Дифференциальное уравнение прогиба балки имеет вид
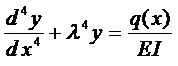 ,
,
где l упругая постоянная, характеризующая свойства основания, Е - модуль упругости балки, I - момент инерции площади поперечного сечения балки, q (x) - интенсивность внешней нагрузки.
Этому уравнению соответствует однородное уравнение
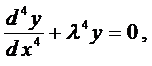
для которого характеристическое уравнение имеет вид
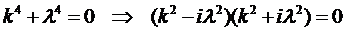 .
.
Непосредственно легко проверить, что его корнями являются
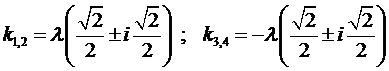 .
.
Этим корням соответствует общее решение
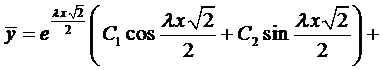 .
.
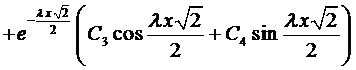 .
.
Рассмотрим случай, когда 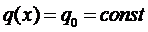 .
.
Тогда частное решение будем искать в виде 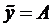 . Подставим это выражение в уравнение прогиба балки, получим
. Подставим это выражение в уравнение прогиба балки, получим 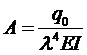 .
.
Тогда
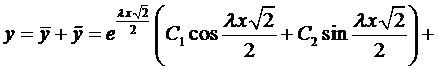
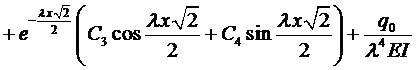 . (6)
. (6)
Константы 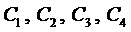 определяются из условий закрепления концов балки, так, например, если концы балки закреплены жестко, то эти условия (граничные условия) имеют вид
определяются из условий закрепления концов балки, так, например, если концы балки закреплены жестко, то эти условия (граничные условия) имеют вид
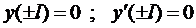 .
.
Подставляя в эти граничные условия полученное выражение для прогиба (6), получим систему четырёх уравнений для определения 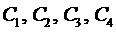 .
.
Лекция № 44. Тема 6: Системы дифференциальных уравнений
6.1. Нормальные системы дифференциальных уравнений
К решению систем дифференциальных уравнений приводят, в частности, задачи по исследованию колебательных процессов в технике, физике, меха-нике. Вибрации сооружений, электромагнитные колебания, колебания упру-гих тел - все эти процессы описываются системами дифференциальных уравнений.
В качестве примера рассмотрим движение материальной точки массой т в плоскости О ху. Согласно второму закону Ньютона имеем
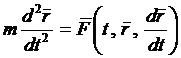 .
.
Спроектируем векторное равенство на координатные оси
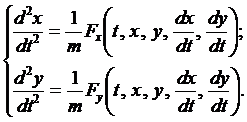 (1)
(1)
Получена система дифференциальных уравнений относительно двух неизвестных функций 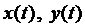 , которые определяют положение точки на плоскости. Здесь t - время,
, которые определяют положение точки на плоскости. Здесь t - время,
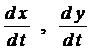 - проекции скорости,
- проекции скорости,
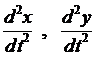 - проекции ускорения на координатные оси.
- проекции ускорения на координатные оси.
Будем рассматривать системы дифференциальных уравнений, каждое уравнение которой разрешено относительно старшей производной – канонические системы. Такую систему, путём введения дополнительных функций, всегда можно привести к эквивалентной ей системе дифференциальных уравнений первой порядка (ДУ-1), разрешенных относительно производной.
Например, приведём систему (1) к системе ДУ-1.
Введём функции 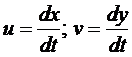 . Тогда она примет вид
. Тогда она примет вид
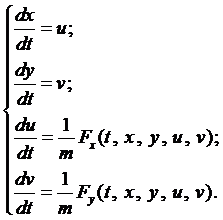
Поэтому в дальнейшем будем рассматривать только такие системы.
Определение 1. Нормальной системой дифференциальных уравнений называется система дифференциальных уравнений вида
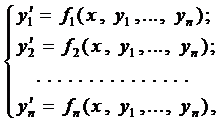 (2)
(2)
где 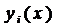 - искомые функции, а
- искомые функции, а 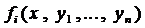 заданные функции в некоторой области G переменных
заданные функции в некоторой области G переменных 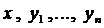 .
.
Определение 2. Решением системы (2) называется совокупность п дифференцируемых функций: 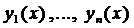 , которые при подстановке в систему ДУ, обращают каждое уравнение в тождество.
, которые при подстановке в систему ДУ, обращают каждое уравнение в тождество.
Определение 3. Совокупность функций 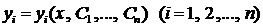 называется общим решением системы ДУ (2), если:
называется общим решением системы ДУ (2), если:
1. Эти функции являются решением системы при любых значениях 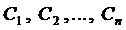 ;
;
2. Для любых начальных условий вида
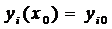 (3)
(3)
из области G можно найти такие значения 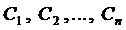 , при которых каждая функция этой совокупности удовлетворяет условиям (3).
, при которых каждая функция этой совокупности удовлетворяет условиям (3).
Задача Коши для системы (2) формулируется следующим образом: Найти такое решение 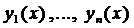 , которое удовлетворяет начальным условиям (3).
, которое удовлетворяет начальным условиям (3).
Теорема (о существовании и единственности решения задачи Коши).
Если правые части системы ДУ (2) и их частные производные по переменным 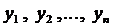 непрерывны в области G, то для любой точки
непрерывны в области G, то для любой точки 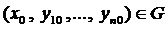 существует единственное непрерывное решение задачи Коши, удовлетворяющее начальным условиям (3).
существует единственное непрерывное решение задачи Коши, удовлетворяющее начальным условиям (3).
Пример 1*. Определить траекторию полёта снаряда, выпущенного из орудия под углом a к горизонту со скоростью V 0. Сопротивлением воздуха пренебречь.
Вначале лекции были рассмотрены общие уравнения (1), которые можно применить для данной задачи
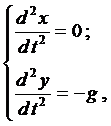
где g - ускорение свободного падения. Проинтегрируем каждое уравне-ние системы
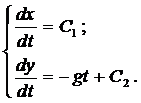
Константы интегрирования 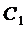 и
и 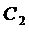 найдем из начальных условий:
найдем из начальных условий:
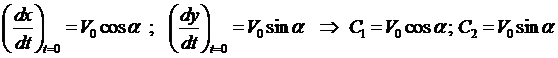 .
.
Тогда система примет вид
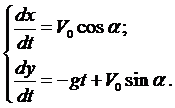
Ещё раз проинтегрируем
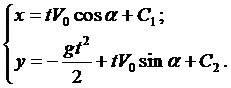
Константы интегрирования 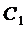 и
и 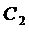 определим из начальных условий с учетом выбора начала системы координат в положении орудия:
определим из начальных условий с учетом выбора начала системы координат в положении орудия:
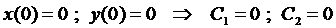 .
.
Таким образом, решением системы являются функции
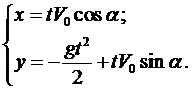
Исключая параметр t, приходим к уравнению траектории
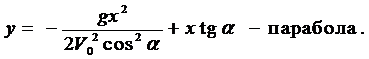
6.2. Решение нормальных систем ДУ методом исключений
Решение системы (2) сводится к решению ДУ- п методом исключений.
Продифференцируем по х первое уравнение системы (2)
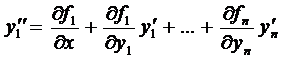 .
.
С учетом остальных уравнений системы это выражение примет вид
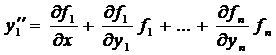 или
или 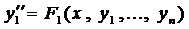 .
.
Аналогично, ещё раз продифференцировав, получаем
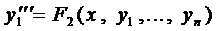
и т. д., пока не найдём п -ую производную
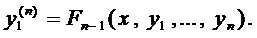
Таким образом, получаем систему п уравнений
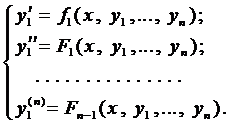 (4)
(4)
Из первых п - 1 уравнений системы (4) выразим 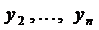 через переменные
через переменные 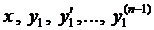 . Подставляя их значения в последнее урав-нение системы (4), имеем
. Подставляя их значения в последнее урав-нение системы (4), имеем
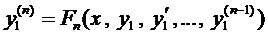 . (5)
. (5)
Решая уравнение (5), находим 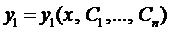 , а с помощью выражений для
, а с помощью выражений для 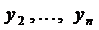 определяем и эти функции.
определяем и эти функции.
Замечание 1. Из приведённых выше рассуждений видна структура общего решения системы дифференциальных уравнений (2).
Замечание 2. Часто систему уравнений можно сразу сводить к уравнению (5), минуя систему (4). В частности, это относится к линейным системам дифференциальных уравнений.
Пример 2. Найти общее решение системы
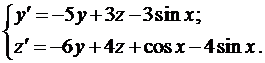
Из первого уравнения найдем
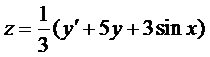
и подставим во второе уравнение
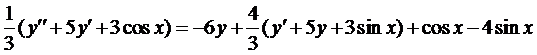 .
.
Умножим на 3 и приведём подобные члены
 .
.
Составим характеристическое уравнение
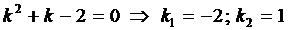 .
.
Имеем
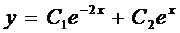 .
.
Тогда, с учетом выражения для z, получаем
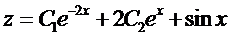 .
.
Пример 3. Решить задачу Коши
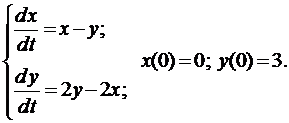
Из первого уравнения находим
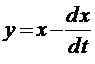
и подставляем во второе уравнение
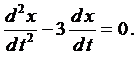
Составим характеристическое уравнение
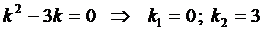 .
.
Тогда
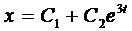
и
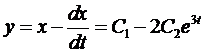 .
.
Из начальных условий получаем систему для нахождения 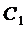 и
и 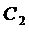
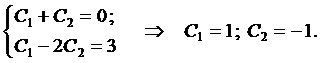
Окончательно имеем
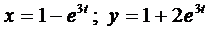 .
.






