ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 3 страница

де

В случае, если плоская фигура ограничена сверху кривой , а снизу – кривой , то

О а b

3.1.2. Площадь фигуры, если ее граница задана параметрическими уравнениями.

Пусть для криволинейной трапеции линия задана параметрическими уравнениями: при этом . Тогда, делая замену в интеграле, получаем

(1)

Пример 1. Найти площадь эллипса .

Запишем параметрические уравнения эллипса 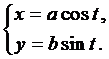Тогда по формуле (1) в силу симметрии получим

3.1.3. Площадь в полярной системе координат

(площадь криволинейного сектора).

Рассмотрим фигуру, ограниченную двумя

лучами: , выходящими из полюса

и кривую . Определим её площадь.

Для этого разобьём её на п секторов с О P

площадью

Составим интегральную сумму

, (2)

где .

Переходя к пределу в формуле (2) при , имеем

(3)

Пример 2. Найти площадь кардиоиды

В силу симметрии, с учетом формулы (3),

получаем

-2 а О

3.2. Длина дуги плоской кривой

3.2.1. Кривая задана в ДСК.

Определим длину дуги АВ. Впишем в неё ломаную, длина которой

О а b

Воспользуемся теоремой Лагранжа: , где . Тогда

. (4)

Пример 3. Найти длину дуги линии при .

3.2.2. Линия задана параметрическими уравнениями.

Линия задана уравнениями и пусть . Тогда, заменяя переменную в интеграле (4), с учетом значе-ния производной от функции, заданной параметрическими уравнениями, из формулы (4) следует

(5)

Замечание. Выражения назы-ваются дифференциалами дуги.

Пример 4. Найти длину развертки окружности

Согласно формуле (5) получаем

3.2.3. Линия задана в полярной системе координат.

Рассматривая как параметр с учетом, что и , получаем

Тогда из формулы следует

. (6)

Пример 5. Найти длину кардиоиды .

В силу симметрии по формуле (6) получаем

3.3. Площадь поверхности тела вращения

Пусть линия вращается вокруг оси О х.

Определим площадь

поверхности вращения. у

Разобьём на п

частей и впишем ломаную

в график . Тогда каждая

хорда опишет боковую

поверхность усеченного х

конуса с площадью О а b

Учитывая, что при , и переходя к пределу в интегральной сумме, получим

(7)

Пример 6. Найти площадь поверхности сферы .

Рассмотрим сферу как поверхность, образованную вращением полу-

окружности вокруг оси О х. Тогда и по формуле (7) имеем

3.4. Вычисление объёма тела по площадям поперечных сечений

Пусть нам известна площадь любого сечения тела плоскостью, перпендикулярной оси О х: .

а b х

Составим интегральную сумму . Тогда

(8)

Следствие. Если тело получено путём вращения криволинейной трапеции вокруг оси О х, то из формулы (8) следует

(9)

Аналогично, если тело получено путём вращения вокруг оси О у, то

Пример 7. Найти объём шара .

Рассмотрим шар как тело, образованное вращением полукруга вокруг оси О х. Тогда по формуле (9) получаем

Лекция № 32

3.5. Приложения определённого интеграла к некоторым задачам физики

Приложения определённого интеграла к задачам физики рассмотрим на двух показательных примерах, решения которых представляют собой общую идею решения подобных задач.

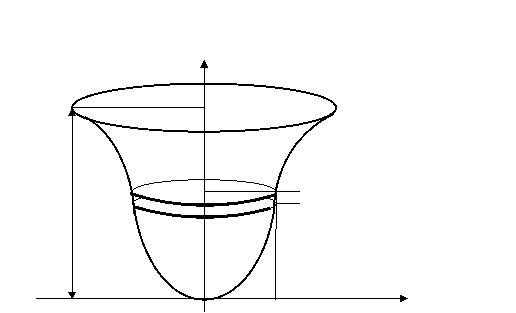Задача 1. Определить работу, затраченную на откачку жидкости из резервуара, имеющего форму поверхности, полученную при вращении линии

вокруг оси О у.

Н у

О х

Работа при подъёме элементарного объёма жидкости

где - плотность жидкости, Н - глубина резервуара. Тогда

где - обратная функция к функции .

Задача 2. Определить давление жидкости на вертикальную пластину, имеющую форму равнобочной трапеции, у которой большее основание совпадает с уровнем жидкости.

a - b

x y

xxxxxxxxxxxxxxxxxxx h

Давление жидкости на элементарную полоску . Из подобия треугольников определим

Тогда интегрируя, получаем

Тема 4: Несобственные интегралы

4.1. Несобственные интегралы первого рода (с бесконечными пределами)

Пусть дан интеграл с фиксированным нижним пределом интегри-рования а

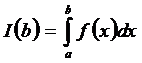Рассмотрим его поведение при .

Определение 1. Если существует конечный предел , то этот предел называется несобственным интегралом первого рода от функции на и обозначается

(1)

В этом случае интеграл называется сходящимся. Если же предел (1) не существует или равен бесконечности, то такой интеграл называется расходящимся.

Аналогично определяются несобственные интегралы и для других бесконечных интервалов:

Если известна первообразная функции , то

(2)

Пример 1. Исследовать сходимость интеграла .

По формуле (2) получаем

Пример 2. Исследовать сходимость интеграла

Согласно определению несобственного интеграла из таблицы неопре-делённых интегралов получим

Таким образом, интеграл сходится, если степень и расходится, если .

Если первообразная функции не известна, то при исследовании несобственного интеграла на сходимость применяют признаки сравнения:

Теорема 1. Пусть 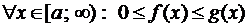, тогда

- если сходится, то сходится и ,

- если расходится, то расходится и .

В силу свойства определённого интеграла, интегрируя данное нера-венство, получаем

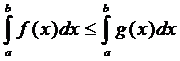Переходя к пределу при , приходим к неравенству

Аналогично доказывается вторая часть теоремы.

Пример 3. Исследовать на сходимость .

Таким образом, интеграл сходится. Неравенство было получено с использованием свойства 7 об оценке интеграла.

Теорема 2. Если .

Доказательство аналогичное.

В этом случае интеграл называется абсолютно сходящимся. Если , а 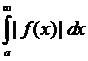расходится, то интеграл называется условно сходящимся.

Например, интеграл является абсолютно сходящимся, так как

Интеграл - условно сходящийся.

4.2. Несобственные интегралы второго рода (от разрывных функций)

Если функция на имеет конечное число точек разрыва первого рода, то вычисление интеграла от такой функции трудности не представляет. Например, если - точка разрыва первого рода, тогда

Если же функция имеет бесконечный разрыв, то в этом случае интеграл называется несобственным второго рода. Тогда, если - точка разрыва второго рода, то интеграл определяется следующим образом

Аналогично определяются несобственные интегралы от функций с разрывами в точках и :

Если для несобственного интеграла от разрывной функции в точке известна первообразная , то его сходимость зависит от существования значения .

Пример 4. Исследовать сходимость .

Таким образом, интеграл сходится, если степень и расходится, если .

Если же первообразная функции не известна, то для исследования сходимости, как и для несобственных интегралов первого рода, исполь-зуются аналогичные признаки сравнения.

Пример 5. Исследовать на сходимость интеграл и, если он сходится, вычислить его.

Замечаем, что в точке подынтегральная функция имеет разрыв второго рода, а интеграл запишем в виде

Сравним подынтегральную функцию с эталонной функцией .

Тогда показатель р степени у подынтегральной функции равен , следовательно интеграл сходится. Вычислим его

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Лекция № 33. Тема 1: Предел. Непрерывность. Частные производные

1.1. Определение функции нескольких переменных

Остановимся, в основном, на случае функции двух переменных. Определения и полученные результаты легко распространить и на случай большего числа переменных.

Рассмотрим плоскость О ху - множество всех точек .

Определение 1. Множество всех точек , координаты которых удовлетворяют неравенству , называется -окрест-ностью точки и обозначается .

Определение 2. Областью D называется множество точек, обладающих свойствами:

1. Любая точка принадлежит ей и вместе с некоторой - окрестностью (свойство открытости);

2. Любые точки и можно соединить непрерывной линией, целиком принадлежащей D (свойство связности).

Линия, ограничивающая данную область, называется границей. Если к области отнести и точки границы, то такая область называется замкнутой.

М ₁ М ₂

Определение 3. Если каждой паре значений двух независимых переменных из некоторой области D соответствует по некоторому правилу или закону определённое значение величины z, то z называется функцией двух переменных в области D, и пишут .