Пример 1. 
Замечание 1. Если выражение под знаком радикала линейное, т.е. имеет вид 
, то из свойства 4 следует, что мы вправе применить тот же подход.
Пример 2. 
1.10.2. Интегралы вида 
.
Аналогично, если 
, то подстановка 
также приводит к интегрированию рациональных дробей.
Пример 3. 
.
1.10.3*. Интегралы вида 
.
Преобразуем выражение под знаком радикала. Если за знак радикала вынести 
, то получим 
. Выполнив замену 
, приходим к трём случаям:
Рассмотрим каждый из этих случаев отдельно. Естественно, случай 
не рассматривается.
1. Интегралы вида 
.
Заменой 
такие интегралы приводятся к интегралам от рациональной функции.
Пример 3. 
.
2. Интегралы вида 
В этом случае используется замена 
.
Пример 4. 
.
3. Интегралы вида 
.
Рационализация подынтегрального выражения достигается заменой 
.
Пример 5. 
1.11. Понятие о неберущихся интегралах
Теорема существования неопределённого интеграла утверждает, что всякая 
, непрерывная на 
, имеет на этом интервале первообразную. Однако из этого не следует, что интеграл от любой элементарной функции выражается через элементарные функции. Такие интегралы называются неберущимися в элементарных функциях. Они порождают новые, неэлементарные функции.
К таким интегралам, например, относятся:
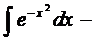интеграл Пуассона;
- интегральные синус и косинус;
- интегралы Френеля;
- интегральный логарифм и многие другие.
Существуют другие методы для их нахождения с использованием так называемых специальных функций, функциональных рядов и т.п.
Лекция № 29. Тема 2: Определённый интеграл
2.1. Задачи, приводящие к понятию определённого интеграла
1. Задача о площади криволинейной трапеции.
Пусть на 
задана функция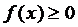 
. Требуется найти пло-щадь S фигуры, образованной осью O x, прямыми: 
и графиком функции 
(криволинейная трапеция).
у
x
О а х i - 1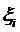 
xi b
Разобьём на п частей: 
. На каждом участке разбиения 
выберем точку 
и составим сумму
, где 
. (1)
Тогда 
, так как S п геометрически представляет собой площадь ступенчатой фигуры. Если теперь перейти к пределу в формуле (1), когда 
, то получим значение площади криволинейной трапеции, т.е.
.
2. Задача о массе тела.
Задан линейный неоднородный стержень с плотностью 
, лежащий в пределах . Требуется определить его массу М. Аналогично разобьём его на части. Так как в пределах 
плотность изменяется мало, то 
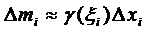, а масса стержня
.
Точное значение массы получим, если перейти к пределу, когда .
.
2.2. Определение определённого интеграла
Пусть на задана функция . Разделим на части произвольным образом точками: 
. На каждом из полученных отрезков разбиения 
произвольно выберем точку 
и составим сумму
, где 
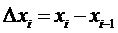, (2)
называемую интегральной суммой функции на отрезке .
Определение 1. Если предел интегральной суммы (2) не зависит от способа разбиения отрезка и выбора точек 
, то он называется опре-делённым интегралом от функции на отрезке и обозначается
, (3)
где а - нижний, b - верхний пределы интегрирования.
Определение 2. Если для на существует предел (3), то функция называется интегрируемой на .
При каких условиях существует предел (3)?
Теорема 1 (теорема существования определённого интеграла). Если непрерывна на , то она интегрируема на .
Замечание. Среди разрывных функций на есть как интегри-руемые (ограниченные монотонные), так и неинтегрируемые. Например, неинтегрируемой является функция Дирихле
D (x) = 
Действительно, если в качестве точек выбрать рациональные точки и рассмотреть функцию Дирихле на отрезке 
, то из формулы (3) следует
а если выбрать иррациональные точки, то
Таким образом, предел (3) не существует.
Теперь выясним геометрический смысл определённого интеграла:
Из ранее рассмотренной задачи при 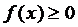- это площадь криволинейной трапеции. При 
- это тоже площадь, но со знаком минус. Поэтому определённый интеграл – это алгебраическая площадь криволинейной трапеции.
у
х
-
Физический смысл определённого интеграла.
Из ранее рассмотренной задачи масса стержня с линейной плотностью определяется как 
.
Аналогично рассуждая, получаем: если 
- сила, действующая вдоль прямолинейного участка , то работа этой силы 
.
2.3. Основные свойства определённого интеграла
1. Если 
.
Действительно, 
.
2. Свойство линейности. Если функции и 
интегрируемые на и 
, то
.
Это свойство вытекает из определения определённого интеграла.
3..
Это свойство следует из того, что в интегральной сумме все разности 
меняют знак.
4..
Действительно, так как 
.
5. Свойство аддитивности. Если 
, то
Это следует из определения определённого интеграла, если в качестве точки разбиения взять точку с.
Если.
Действительно, так как в интегральной сумме все слагаемые больше или равны нулю.
7. Если на функции и удовлетворяют неравенству 
, то
.
Действительно, если рассмотреть разность, то с учетом свойства 6, получаем
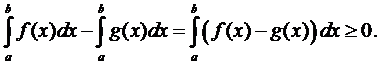
8. 
.
Проинтегрировав очевидное неравенство 
, приходим к данному свойству.
9. Оценка определённого интеграла. Если т и М - наименьшее и наибольшее значения непрерывной функции на , то
Интегрируя неравенство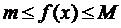 
с учетом свойств 1 и 7, получаем данное свойство.
10. Теорема о среднем. Если функция непрерывна на , то существует такая точка 
, для которой выполняется равенство
.
Из свойства 8 получаем неравенство 
.
Так как непрерывна на , то она принимает все значения, заключенные между т и М. Из этого и следует данное свойство.
2.4. Интеграл как функция верхнего предела
Если в определённом интеграле 
зафиксировать нижний предел интегрирования, а верхний считать переменным, то интеграл будет являться функцией верхнего предела 
, где 
.
Найдем производную этой функции.
Теорема 2 (Барроу). Если непрерывная функция, то
.
Дадим переменной х приращение 
, тогда
.
По теореме о среднем получаем
, (1)
где 
.
Из формулы (1) следует, что функция 
непрерывная, так как
С учетом этой формулы находим производную
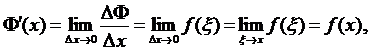
что следует в силу непрерывности функции .
Лекция № 30
2.5. Формула Ньютона – Лейбница
Теорема 1. Если функция первообразная для функции , то
. (1)
С учетом теоремы Барроу функция будет являться первообразной и тогда из теоремы о первообразных следует
.
Положим в этом равенстве 
. Тогда имеем
.
Полагая 
, получаем формулу Ньютона – Лейбница
.
Пример 1. Оценить 
.
Для подынтегральной функции нетрудно найти: 
и 
. Тогда
Теперь вычислим интеграл непосредственно по формуле Ньютона – Лейбница
т.е. 
Пример 2. Найти среднее значение функции 
на отрезке 
.
По теореме о среднем имеем
2.6. Замена переменной в определённом интеграле
Пусть дан интеграл 
, где подынтегральная функция непрерывна на . Рассмотрим функцию 
, которая имеет непре-рывную производную на 
и 
.
Тогда имеет место формула замены переменной в определённом интеграле
(2)
Докажем эту формулу.
С одной стороны 
а с другой стороны
Замечание 1. Аналогично, как и для неопределённого интеграла, часто более удобно использовать замену 
.
Замечание 2. При вычислении определённого интеграла по формуле (2) не нужно возвращаться к “старой“ переменной.
Замечание 3. Полезно отметить свойства определённого интеграла от четных и нечетных функций в симметричных пределах интегрирования:
1. Если - четная функция, то
(Далее по определению четной функции) = 
2. Если - нечетная функция, то
(Далее по определению нечетной функции) = - 
Пример 3. Вычислить 
.
Сделаем замену 
.
Тогда для нижнего предела интегрирования 
получаем 
, а для верхнего предела интегрирования 
.
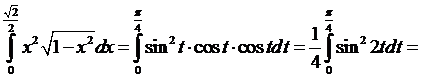
Пример 4. Вычислить 
.
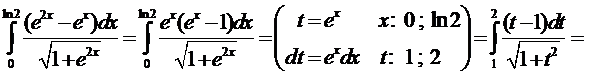
2.7. Интегрирование по частям в определённом интеграле
Если соответствующие интегралы существуют, то проинтегрируем от а до b формулу
.
Получим формулу интегрирования по частям
(3)
Замечание 4. Выражения для и и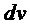 
выбираются из таких соображе-ний, чтобы интеграл в правой части формулы (3) был известен.
Пример 5. 
.
Аналогично, как и для неопределённого интеграла, формулу интегрирования по частям можно применять для вычисления интеграла неоднократно.
Пример 6.
Лекция № 31. Тема 3: Приложения определённого интеграла
3.1. Площадь плоской фигуры
3.1.1. Площадь фигуры в ДСК.
Как известно, площадь криволинейной трапеции 
, если 
. Если же 
- знакопеременная функция, то
