ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Лекция № 25. Тема 1: Неопределённый интеграл
1.1. Первообразная и неопределённый интеграл
Ранее для заданной функции  мы находили производную
мы находили производную  . Теперь рассмотрим обратную задачу: Известна производная
. Теперь рассмотрим обратную задачу: Известна производная  . Требуется найти
. Требуется найти  , которая называется первообразной.
, которая называется первообразной.
С точки зрения механики – по скорости требуется восстановить движение материальной точки.
Определение 1. Функция  называется первообразной на некотором промежутке
называется первообразной на некотором промежутке  для функции
для функции  , если
, если  для всех х из этого промежутка.
для всех х из этого промежутка.
Пример 1. Если  , то
, то  получаем
получаем 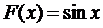 , так как
, так как  . Кроме того, замечаем, что первообразными будут являться также функции
. Кроме того, замечаем, что первообразными будут являться также функции  и т.д.
и т.д.
Таким образом, первообразные отличаются на константу.
Теорема. Если 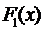 и
и  первообразные на
первообразные на  , то
, то  выполняется
выполняется  , где
, где  .
.
Обозначим  и применим к этой функции теорему Лагранжа:
и применим к этой функции теорему Лагранжа:  , так как
, так как  , то
, то  .
. 
Замечание 1. Если первообразную определить на некотором множестве, а не промежутке, то данная теорема, вообще говоря, неверна, что видно из примера:
Две функции  являются первообраз-ными для функции
являются первообраз-ными для функции 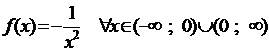 . Однако, их разность
. Однако, их разность 

Определение 2. Множество всех первообразных на некотором проме-жутке называется неопределённым интегралом от функции  и обозна-чается
и обозна-чается
 .
.
Выражение  называется подынтегральным. Операция нахождения неопределённого интеграла называется интегрированием функции
называется подынтегральным. Операция нахождения неопределённого интеграла называется интегрированием функции  .
.
С геометрической точки зрения неопределённый интеграл представляет собой множество кривых  , получаемых путём сдвига одной из них параллельно самой себе вдоль оси О у.
, получаемых путём сдвига одной из них параллельно самой себе вдоль оси О у.
1.2. Основные свойства неопределённого интеграла
1.  .
.
Действительно,  .
.
2.  .
.
Действительно,  .
.
3. Свойство линейности:  , где
, где  .
.
Продифференцируем обе части этого равенства.
Для левой части получаем  .
.
Для правой:  .
.
4.  , где
, где  .
.
Доказывается аналогично дифференцированием.
1.3. Таблица неопределённых интегралов
Непосредственным дифференцированием можно проверить следующие формулы:
1. 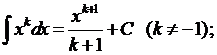 4.
4. 
2.  5.
5. 
3.  6.
6. 
7.  11.
11. 
8.  12.
12. 
9. 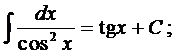 13.
13. 
10.  14.
14. 
Замечание 2. Используя свойство 4, таблицу неопределённых интегралов можно расширить. Например,  .
.
С помощью этой таблицы можно находить некоторые интегралы.
Пример 2.
 .
.
Пример 3.
 .
.
1.4. Интегрирование методом замены переменной (способ подстановки)
Пусть функция  является дифференцируемой и имеет обратную функцию
является дифференцируемой и имеет обратную функцию  . Тогда имеет место формула, которая проверяется дифференцированием:
. Тогда имеет место формула, которая проверяется дифференцированием:
 . (1)
. (1)
Действительно, продифференцируем левую часть:  ,
,
Затем продифференцируем правую часть
 = (по правилу дифференцирования сложной функции) =
= (по правилу дифференцирования сложной функции) =  = (по правилу дифференцирования обратной функции) =
= (по правилу дифференцирования обратной функции) =  .
.
Замечание 3. Функцию  следует выбирать так, чтобы интеграл в правой части формулы (1) можно было найти.
следует выбирать так, чтобы интеграл в правой части формулы (1) можно было найти.
Замечание 4. В практике нахождений интегралов константу С не пишут для каждого интеграла, так как они в конечном итоге будут входить в окончательный ответ, содержащий произвольную константу.
Замечание 5. Часто более целесообразно применять замену переменной в виде  . Это в том случае, когда интеграл можно представить в виде
. Это в том случае, когда интеграл можно представить в виде  . Например,
. Например,
 .
.
Пример 4. 



 .
.
Пример 5.  .
.
Пример 6.

Пример 7. Найдите ошибку:
На основании свойства 4 имеем
 .
.
С другой стороны

Отсюда следует

Лекция № 26
1.5. Интегрирование некоторых функций, содержащих квадратный трёхчлен
Рассмотрим интегралы вида  . Они с помощью замены
. Они с помощью замены  приводятся к известным интегралам.
приводятся к известным интегралам.
Пример 1. 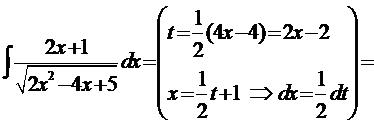


 .
.
Замечание 1. Если для первого из рассмотренных интегралов квадрат-ный трёхчлен имеет действительные корни, то более целесообразно преобразовать подынтегральную функцию, представив её как сумму алгебраических дробей со знаменателями–множителями в разложении квадратного трёхчлена. Более подробно об этом будет рассмотрено в следующей лекции.
Пример 2. Найти интеграл  .
.
Преобразуем подынтегральную функцию:
 .
.
Определим коэффициенты А и В, выполнив сложение дробей и приравняв числители дробей правой и левой частей равенства:
 .
.
Приравнивая коэффициенты при х и свободные члены, получим

откуда  .
.
Тогда имеем

1.6. Интегрирование по частям
Пусть u и v дифференцируемые функции. Тогда справедлива формула
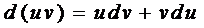 . (1)
. (1)
Проинтегрировав выражение (1), получаем формулу интегрирования по частям
 . (2)
. (2)
Формула (2) применяется при нахождении интегралов от функций вида:

и некоторых других.
Пример 3. 
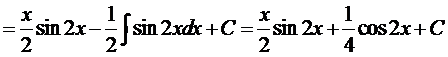 .
.
Пример 4. Найти интеграл  . Воспользуемся формулой (2) дважды.
. Воспользуемся формулой (2) дважды.



1.7. Многочлены и рациональные дроби
Вначале напомним некоторые положения из алгебры.
Рассмотрим многочлен п -ой степени  с действительными коэффициентами. Если
с действительными коэффициентами. Если  , то
, то  называется корнем многочлена. Согласно основной теоремы алгебры любой такой многочлен можно представить в виде
называется корнем многочлена. Согласно основной теоремы алгебры любой такой многочлен можно представить в виде
 (3)
(3)
где  действительные корни кратности
действительные корни кратности  , квадратичные множители в формуле (3) действительных корней не имеют и
, квадратичные множители в формуле (3) действительных корней не имеют и  .
.
Пример 5. Представить в виде (3) многочлен  .
.


Здесь 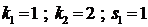 и
и  .
.
Определение 1. Рациональной функцией или дробью называется функция вида
 . (4)
. (4)
При этом будем считать, что  (это всегда можно сделать путём деления числителя и знаменателя на
(это всегда можно сделать путём деления числителя и знаменателя на  ) и
) и  . Такая рациональная дробь называется правильной рациональной дробью.
. Такая рациональная дробь называется правильной рациональной дробью.
В противном случае, нужно выделить целую часть, разделив числитель на знаменатель, т.е. представить дробь в виде
 ,
,
где  - многочлен степени
- многочлен степени  , а
, а  - многочлен степени меньше
- многочлен степени меньше  .
.
Пример 6. Выделить целую часть неправильной рациональной дроби
 .
.
Выполним деление многочленов 


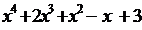


Таким образом, дробь можно представить в виде
 .
.
Определение 2. Рациональные дроби вида
1.  ; 2.
; 2.  3.
3.  4.
4. 
называются простейшими дробями.
Интегралы от дробей 1-2 являются табличными. Интеграл от дроби 3 был уже рассмотрен в пункте 1.5. Интеграл от последней дроби путём замены  приводится к известному интегралу и интегралу вида
приводится к известному интегралу и интегралу вида  , для вычисления которого с помощью формулы интегри-рования по частям можно получить рекуррентную формулу
, для вычисления которого с помощью формулы интегри-рования по частям можно получить рекуррентную формулу
 .
.
Например, если  , то имеем
, то имеем
 .
.
Таким образом, нахождение интегралов от простейших дробей не представляет принципиальных трудностей.
В алгебре доказывается следующая теорема.
Теорема. Если в правильной рациональной дроби знаменатель можно представить разложением (3), то её можно разложить на сумму простейших дробей, т.е.

 .
.
С использованием этой теоремы преобразуется подынтегральная рациональная функция и нахождение интеграла приводится к интегрированию простейших дробей. Коэффициенты в числителях этих дробей вычисляются методом неопределённых коэффициентов.
Пример 7. Для выражения, полученного в примере 6, имеем
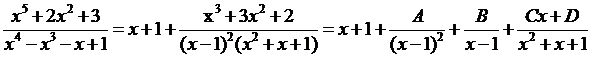 .
.
Коэффициенты  определим методом неопределённых коэф-фициентов. Выполним сложение дробей и приравняем числители правильной дроби в левой части и результата сложения дробей (числителя) в правой части
определим методом неопределённых коэф-фициентов. Выполним сложение дробей и приравняем числители правильной дроби в левой части и результата сложения дробей (числителя) в правой части
 .
.
Приравняв коэффициенты при одинаковых степенях х, получаем систему линейных уравнений

из которой следует  . Окончательно получим
. Окончательно получим
 .
.
Лекция № 27
1.8. Интегрирование рациональных дробей
На основании рассмотренной в предыдущей лекции теоремы преобра-зуется подынтегральная рациональная функция и нахождение интеграла сводится к интегрированию простейших дробей. Коэффициенты в числи-телях этих дробей вычисляются методом неопределённых коэффициентов.
Пример 1.  .
.
Преобразуем подынтегральную функцию, представив её как сумму простейших дробей
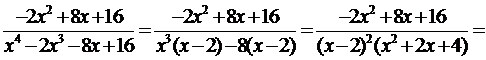
 .
.
Определим коэффициенты  . Для этого приведём дроби в правой части равенства к общему знаменателя и приравняем числители дробей в правой и левой частей полученного равенства
. Для этого приведём дроби в правой части равенства к общему знаменателя и приравняем числители дробей в правой и левой частей полученного равенства
 .
.
Приравнивая коэффициенты при одинаковых степенях х (метод неопределённых коэффициентов), приходим к системе
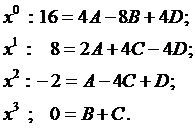
Упростим систему, учитывая, что  ,
,

Из первых двух уравнений получаем  , из первого и третьего -
, из первого и третьего -  и
и  ,
, 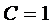 .
.
Тогда наш интеграл приводится к нахождению интегралов


 .
.
1.9. Интегрирование тригонометрических функций
1.9.1. Интегралы вида  , где R - рациональная функция,
, где R - рациональная функция,
приводятся к интегралу от рациональной функции путём замены  , которая называется универсальной тригонометрической подстановкой. Это достигается тем, что
, которая называется универсальной тригонометрической подстановкой. Это достигается тем, что  и
и  выражаются через
выражаются через  рационально:
рационально:
 (1)
(1)
Пример 2.  (воспользуемся формулами (1)) =
(воспользуемся формулами (1)) =

 .
.
Замечание. Использование такой подстановки часто приводит к громоздким выражениям. Эта подстановка, как правило, эффективна, если  и
и  входят в дробное выражение в первой степени.
входят в дробное выражение в первой степени.
1.9.2. Интегралы вида  с помощью подстановок:
с помощью подстановок:  соответственно приводятся к интегралам от рациональной функции.
соответственно приводятся к интегралам от рациональной функции.
Пример 3. 
 .
.
1.9.3. Интегралы вида  .
.
В этом случае применяется замена  , так как
, так как  и
и  выражаются через
выражаются через  рационально:
рационально:  , или используются тригонометрические формулы понижения степени.
, или используются тригонометрические формулы понижения степени.
Пример 4. 
 .
.
1.9.4. Интегралы вида  , где среди показателей т и п по крайней мере одно нечетное.
, где среди показателей т и п по крайней мере одно нечетное.
В этом случае за новую переменную  принимается та функция, которая содержит чётную степень, либо любая, если все функции в нечётных степенях.
принимается та функция, которая содержит чётную степень, либо любая, если все функции в нечётных степенях.
Пример 5. 
 .
.
1.9.5. Интегралы вида  .
.
Эти интегралы находятся с использованием формул:



Пример 6.
 .
.
Лекция № 28
1.10. Интегрирование некоторых иррациональных функций
Рассмотрим только некоторые частные случаи, когда интеграл от иррациональной функции выражается через элементарные функции.
1.10.1. Интегралы вида  .
.
Если 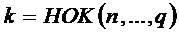 , то подстановка имеет вид
, то подстановка имеет вид  и тогда
и тогда  . После чего интегрирование сводится к интегрированию рациональных дробей.
. После чего интегрирование сводится к интегрированию рациональных дробей.






