КУРС ЛЕКЦИЙ
по высшей математике
Учебное пособие
Донецк - ДонНТУ - 2011
УДК 51 (075.8)
ББК 22.11я73
У 48
Рекомендовано к печати Ученым Советом
ДонНТУ (протокол № 3 от 18.03.11)
Улитин Г.М., Гончаров А.Н. Курс лекций по высшей математике. - Учебное пособие (для студентов всех специальностей). - 2-е изд. - Донецк, ДонНТУ, 2011. – 351 с.
В учебном пособии в соответствии с программой системно изложены лекции для первого и второго курсов обучения высшей математике, которые включают разделы: „Линейная и векторная алгебра”, „Анали-тическая геометрия”, „Введение в анализ функции одной переменной”, „Дифференциальное исчисление”, „Интегральное исчисление”, „Функции нескольких переменных”, „Дифференциальные уравнения”, „Ряды”, „Крат-ные интегралы и элементы теории поля”, „Теория вероятностей и элементы математической статистики”, „Теория функций комплексной переменной”, „Операционное исчисление”.
Краткость лекционного материала в пособии сочетается с вполне приемлемым уровнем строгости и полноты материала. Изложение сопро-вождается решением достаточного количества примеров и задач.
Для студентов высших технических учебных заведений всех специальностей.
Рецензенты: Герасимчук В.С., доктор физ.-мат. наук, профессор, кафедра „Математическая физика” НТУ „КПИ”
Левин В.М., доктор технических наук, профессор, зав.кафедрой высшей и прикладной математики и информатики ДонНАСА
Лесина М.Е., доктор физ.-мат. наук, профессор кафедры высшей математики им. В.В.Пака ДонНТУ
Ó Донецкий национальный технический университет
Ó Улитин Г.М., Гончаров А.Н.
П Р Е Д И С Л О В И Е
В связи с уменьшением аудиторных занятий по высшей математике в технических университетах возникла необходимость более компактного изложения программного материала.
Настоящий курс лекций написан на основе чтения авторами лекций на механическом факультете ДонНТУ, поэтому некоторые рассмотренные вопросы и примеры носят характер приложений к задачам механики. Их количество незначительно и они могут либо совсем не рассматриваться, либо могут быть заменены на соответствующие задачи согласно направ-лениям подготовки студентов. Такие вопросы, а также примеры повышен-ной трудности отмечены знаком *.
Излагаемый материал в данном пособии, по возможности, имеет вид самостоятельных блоков, т.е. каждая лекция имеет завершенную логическую структуру, например, “Определители“, “Кривые второго порядка“, “Непре-рывность функций“ и т.д. Это создаёт для студентов более благоприятные условия для повторения пройденного материала, а также для усвоения пропущенных лекций.
Курс рассчитан на три-четыре семестра при лекционной нагрузке 2-3 часа в неделю. При меньшей нагрузке ряд тем можно не рассматривать, если они не являются основными для выпускающей кафедры, либо вынести их на самостоятельное изучение. Естественно, некоторые темы можно объ-единять или сокращать. Однако все такие преобразования необходимо вы-полнять, не нарушая целостности излагаемого материала. В частности, для отдельных экономических специальностей можно рассмотреть дополни-тельные темы, как например, “Линейные преобразования“, ”Квадратичные формы“, которые можно рассмотреть за счет сокращения некоторых других разделов, например, “Аналитическая геометрия“, „Ряды”, “Кратные инте-гралы“ и исключить ряд приложений к механике и геометрии.
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Лекция № 1. Тема 1: Определители
1.1. Определители второго и третьего порядков
Рассмотрим систему двух линейных алгебраических уравнений с двумя неизвестными
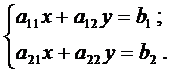(1)
Если первое уравнение системы (1) умножить на а 22 , второе на - а 12 и полученные результаты сложить, то получим
Предположим, что выражение в скобках отлично от нуля, тогда находим
(2)
Аналогично получаем
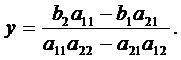(3)
Определение 1. Определителем второго порядка называется выражение, заданное в виде квадратной таблицы из четырех элементов, и определяемое по правилу
(4)
Здесь 
- члены определителя, а 
- элементы определителя.
С учетом определения (4) формулам (2) и (3) можно придать более компактный вид
где 
Пример 1. Вычислить
Аналогично, рассматривая систему трёх уравнений с тремя неиз-вестными, приходим к определению определителя третьего порядка.
Определение 2. Определителем третьего порядка называется выражение, заданное в виде квадратной таблицы из девяти элементов, и определяемое по правилу
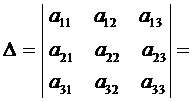
. (5)
Замечание. Выражение (5) является громоздким. Его запомнить будет проще, если использовать следующую схему вычислений
-
Пример 2. Вычислить
1.2. Основные свойства определителей
Все рассмотренные свойства легко проверить непосредственно на примере определителей третьего порядка, хотя они справедливы и в общем случае.
1. При замене столбцов строками с тем же номером (при транспони-ровании) определитель своего значения не меняет, т.е. строки и столбцы у определителя равноправны.
Таким образом, требуется доказать равенство
2. Определитель, содержащий строку (столбец) из нулей, равен нулю.
Действительно, так как в этом случае каждый член определителя содержит множителем элемент этой строки (или столбца), равный нулю.
3. При перестановке двух строк (столбцов) определитель меняет знак.
Доказывается непосредственно, как и свойство 1.
4. Определитель, содержащий две равные строки (столбца), равен нулю.
Сделаем перестановку этих строк. Тогда из свойства 3 получим 
5. Общий множитель всех элементов строки (столбца) можно выносить за знак определителя.
Действительно, это можно сделать, так как этот множитель содержится в каждом члене определителя.
6. Определитель, содержащий две пропорциональные строки (столбцы) равен нулю.
Доказательство этого свойства следует из свойств 4-5.
7. Если все элементы строки (столбца) представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, каждый из которых имеет строку (столбец) из соответствующих слагаемых элементов.
Например,
Доказывается непосредственно, исходя из определения определителя третьего порядка.
8. Если к элементам некоторой строки (столбца) прибавить соответст-вующие элементы другой строки (столбца), умноженные на одно и то же число, то определитель своего значения не изменит.
Доказательство следует из свойств 6-7.
1.3. Вычисление определителей
Определение 3. Алгебраическим дополнением 
некоторого эле-мента данного определителя называется определитель, получаемый при вычеркивании из данного определителя строки и столбца, содержащих этот элемент, и взятый со знаком 
.
Пример 1. Найти 
и 
определителя 
Тогда имеет место следующая
Теорема. Пусть в некотором определителе произвольно выбрана строка (столбец). Тогда сумма произведений элементов этой строки (столбца) на их алгебраические дополнения равна значению определителя.
Например, для строки 
для столбца 
Приведенные формулы легко доказать непосредственно для любых 
.
Замечание 1. Из теоремы видно, что вычисление определителя третьего порядка сводится к вычислению определителей второго порядка. Анало-гично, исходя из этого факта, можно получить определение определителя п -го порядка через определитель (п - 1)-го порядка.
Например, для определения определителя 4-го порядка имеет место формула
(6)
где 
- определители третьего порядка.
Замечание 2. Используя свойство 8 определителей, можно упростить их вычисление, делая в строке (столбце) все элементы равные нулю, кроме одного.
Пример 3. Вычислить определитель 
.
1 шаг: Прибавим ко 2-ому столбцу третий столбец;
2 шаг: Прибавим к 4-ому столбцу 3-й столбец, умноженный на -2:
В результате во 2-й строке остался один элемент 
, неравный нулю.
Воспользуемся формулой (6):
Лекция № 2. Тема 2: Системы линейных алгебраических уравнений
2.1. Правило Крамера
Рассмотрим систему трёх линейных алгебраических уравнений, когда число неизвестных равно числу уравнений, т.е. систему вида
(1)
где - коэффициенты системы, 
- свободные члены 
, 
- неизвестные.
Будем считать, что определитель системы, составленный из коэффи-циентов системы (главный определитель), отличен от нуля, т.е.
Предположим, что система (1) совместна, т.е. имеет решение. Тогда умножим первое уравнение системы на 
, второе – на 
, третье – на 
и сложим полученные выражения
(2)
Первое выражение в скобках в левой части полученного соотношения (2) представляет собой разложение главного определителя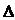 
системы по элементам первого столбца. Остальные выражения в скобках равны нулю, так как представляют собой разложение определителя, имеющего два одинаковых столбца (см. свойство 4). Например,
Тогда из выражения (2) получаем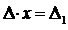 
, где
Аналогично можно получить
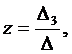(3)
где
Определители 
называются вспомогательными опреде-лителями системы (1).
Покажем теперь, что полученные значения неизвестных (3) на самом деле удовлетворяют системе уравнений (1).
Подставляя выражения (3) в систему (1), получим на примере первого уравнения
Аналогично можно показать и для двух оставшихся уравнений системы.
Таким образом, получаем следующий результат (правило Крамера).
Теорема. Система уравнений (1) с главным определителем 
имеет единственное решение, определяемое по формулам
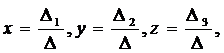
где определители 
получаются из главного определителя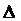 
системы уравнений заменой соответствующего столбца на столбец свобод-ных членов.
Замечание 1. Для системы линейных однородных уравнений
(4)
все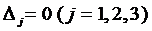 
и тогда, если , то система (4) имеет единст-венное нулевое решение 
Отсюда следует: если система (4) обладает ненулевым решением, то её определитель равен нулю.
Замечание 2. Если же главный определитель системы (1)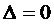 
, тогда возможны следующие два случая:
1. Система несовместна, если, по крайней мере, один из вспомога-тельных определителей отличен от нуля;
2. Если же все определители системы равны нулю, то система либо имеет бесконечное множество решений, что возможно из равенств
либо такая система несовместна, например, в системе уравнений
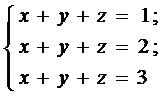
все определители равны нулю, но система несовместна, что следует из ее вида. В этом случае для решения системы уравнений более целесообразно применить метод Гаусса, который будет рассмотрен далее.
Замечание 3. Правило Крамера справедливо для любого числа уравнений системы, т.е. системы вида
Здесь, если 
то 
Пример 1. Используя правило Крамера, решить систему уравнений
Здесь 
откуда получаем 
2.2. Метод Гаусса (метод последовательного исключения неизвестных)
Рассмотрим ту же систему уравнений (1). Пусть коэффициент 
, чего всегда можно достигнуть, переставляя уравнения системы или меняя нумерацию неизвестных. Первое уравнение системы (1) умножим на 
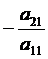и сложим со вторым. Затем первое уравнение умножим на 
и сложим с третьим, тогда получим
(5)
Здесь 
- новые значения коэффициентов, полу-ченные после таких преобразований. Пусть 
, чего можно достигнуть, переставляя два последних уравнения системы. В противном случае, т.е. когда 
, сразу определяем неизвестную z, или получаем несов-местную систему. При таком условии второе уравнение системы (5) умно-жим на 
и сложим с третьим уравнением, тогда получим
(6)
В системе уравнений (6) 
- новые значения коэффициентов и здесь возможны следующие случаи:
1. 
Затем найденное значение z подставляем во второе уравнение системы (6) и определяем у. Из первого уравнения, уже зная у и z, находим х.
2. 
а 
. Тогда система (6) решений не имеет, т.е. система несовместна.
3. 
и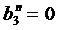 
. В этом случае система (6) принимает вид
(7)
Число уравнений в системе (7) меньше числа неизвестных. Оставим два неизвестных слева, например, х и у, а z перенесем в правую часть системы уравнений (7) и будем считать его произвольным числом. Получим
(8)
Из системы (8) х и у выражаются через z и система имеет беско-нечное множество решений.
Пример 2. Систему уравнений из примера 1 решить методом Гаусса
Первое уравнение умножим на -2 и сложим со вторым уравнением, затем первое уравнение сложим с третьим, получим
или 
Второе уравнение умножим на -3 и сложим с третьим:
Из третьего уравнения получим 
, из второго 
и из первого уравнения 
Пример 3. Методом Гаусса решить систему однородных уравнений
Первое уравнение умножим на -2 и сложим со вторым, затем первое уравнение умножим на -3 и сложим с третьим, получим
откуда
Система имеет бесконечное множество решений. Поэтому в этом случае (см. замечание 1) определитель данной системы уравнений должен быть равен нулю. Проверьте!
Лекция № 3. Тема 3: Матрицы
3.1. Основные виды матриц
Определение 1. Матрицей называется совокупность чисел, располо-женных в т строках и п столбцах и обозначается
Число, стоящее на пересечении 
-ой строки и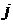 
-го столбца, обозначается и называется элементом матрицы;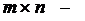 
размерность матрицы.
Существуют следующие виды матриц:
1. Матрица – строка 
2. Матрица – столбец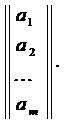 
3. Нулевая матрица - все ее элементы нули.
4. Единичная матрица 
5. Диагональная матрица 
.
6. Симметрическая матрица – для ее элементов выполняется равенство 
для всех 
Важной характеристикой квадратной матрицы А является её опреде-литель, который обозначается 
Если 
, то матрица А назы-вается невырожденной. В противном случае – вырожденной.
Определение 2. Две матрицы 
и 
одинаковой раз-мерности называются равными, если равны все их соответствующие эле-менты 
для всех 
3.2. Действия над матрицами
1. Транспонирование матриц.
Определение 3. Транспонированием матрицы называется замена её строк столбцами с сохранением их номеров.
Транспонированная матрица обозначается А Т.
Пример 1. Найти А Т, если матрица 
Тогда 
2. Сложение матриц.
Определение 4. Суммой двух матриц и одинаковой размерности называется матрица С той же размерности, элементы которой определяются равенствами 
и обозначается 
.
3. Умножение матрицы на число.
Определение 5. Произведением матрицы на некоторое число 
называется матрица , элементы которой равны элементам матрицы А, умноженным на это число , т.е. 
и обозначается 
.
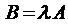Пример 2. Найти матрицу 
, если
4. Умножение матриц.
Определение 6. Произведением матрицы размерности 
и матрицы размерности 
, называется матрица 
, размерности 
, элементы которой удовлетворяют равенству
и обозначается 
.
Замечание 1. Как видно из определения, произведение двух матриц будет определено, если число столбцов первой матрицы равно числу строк второй.
Пример 3. Найти произведение матриц 
Тогда
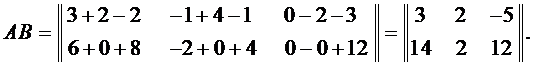
Замечание 2. Легко убедиться в том, что в общем случае произведение матриц не обладает коммутативным свойством, т.е.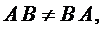 
что видно из следующего примера.
Пример 4. Найти произведение матриц 
Тогда имеем
3.3. Обратная матрица
Определение 7. Обратной матрицей матрицы А называется матрица 
, для которой выполняется равенство 
Из этого определения следует, что понятие обратной матрицы является взаимообратным и определено только для квадратных матриц. При этом для существования обратной матрицы необходимо, чтобы матрица А была невырожденной, т.е. .
Покажем, что обратной матрицей для случая матрицы А размер-ности 
будет матрица
где - алгебраические дополнения элемента .
Тогда
Например, 
и т.д.
Так же можно проверить и равенство 
Замечание 4. Аналогично для матрицы А размерности 
обратная матрица имеет вид
3.4. Решение систем линейных уравнений с помощью обратной матрицы
Рассмотрим систему линейных алгебраических уравнений
(1)
Введем следующие матрицы
Тогда, используя правило умножения матриц, систему (1) можно пред-ставить в следующем виде (матричная форма системы уравнений (1))
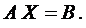(2)
Пусть 
тогда для матрицы А существует обратная 
Умножая обе части равенства (2) слева на , получим
(3)
В силу равенств 
и 
формула (3) принимает вид
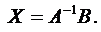(4)
Не трудно убедиться в том, что выражение (4), полученное для Х, действительно является решением уравнения (1). Подставляя это выражение в уравнение (2), имеем
Замечание 5. Решение, полученное по формуле (4), то же самое, что было получено по формулам Крамера. Этот факт, вытекающий из единственности решения системы (1), можно непосредственно проверить, если подставить в формулу (4) выражение для обратной матрицы.
Пример 5. Матричным методом решить систему уравнений
Здесь
Тогда
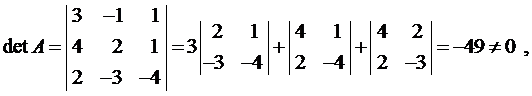
следовательно, обратная матрица существует.
Вычисляем алгебраические дополнения
аналогично далее
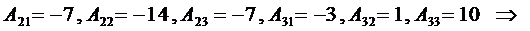
Таким образом, получим окончательное решение
.
Лекция № 4. Тема 4: Общий случай решения систем
линейных алгебраических уравнений
4.1. Ранг матрицы
Определение 1. Минором порядка k называется определитель, состо-ящий из элементов матрицы, которые находятся на пересечении k разных строк и k разных столбцов.
Определение 2. Если в матрице 
все миноры порядка k > r равны нулю, а среди миноров порядка r существует, по крайней мере, один отличный от нуля, то число r называется рангом матрицы и обо-значается 
или 
.
Определение 3. Две матрицы называются эквивалентными, если одна из них получается из другой при помощи следующих преобразований:
1. Перестановка местами двух строк или столбцов матрицы;
2. Умножение всех элементов любой строки или столбца матрицы на одно и то же число, отличное от нуля;
3. Добавление ко всем элементам любой строки или столбца матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Эквивалентность матриц обозначается 
.
Из свойств определителей следует
Теорема 1. Все эквивалентные матрицы имеют один и тот же ранг.
Пользуясь понятием эквивалентности матриц из данной матрицы раз-мерности получают ступенчатую матрицу, т.е. матрицу вида
в которой определитель (минор r порядка)
.
а все остальные миноры порядка больше r равны нулю, так как содержат строки, состоящие из нулей.
Пример 1. Определить ранг матрицы А = 
.
1 шаг: Поменяем местами 1-ю и 2-ю строки;
2 шаг: Прибавим ко 2-ой строке 1-ю строку, умноженную на -2;
к 3-ей строке 1-ю строку, умноженную на -3;
к 4-ой строке 1-ю строку, умноженную на -5;
3 шаг: Прибавим к 3-ей строке 2-ю строку, умноженную на -1;
к 4-ой строке 2-ю строку, умноженную на -2;
4.2. Исследование и решение систем линейных алгебраических уравнений
Рассмотрим систему из т линейных алгебраических уравнений с п неизвестными
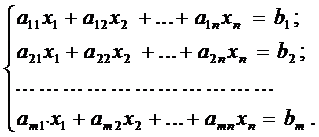(1)
Решению системы (1) должно предшествовать исследование, которое приводит к следующим основным задачам теории систем линейных уравнений:
1. Определить является ли система совместной или несовместной;
2. Если система совместна, то имеет ли она единственное решение или бесконечное множество решений;
3. Если система совместна и имеет единственное решение, то найти это решение;
4. Если система совместна и имеет бесконечное множество решений, то описать всю совокупность решений.
Составим из коэффициентов системы (1) две матрицы
где А – основная матрица, а 
– расширенная матрица.
Ответом на первые два поставленных вопроса является
Теорема 2 (Кронекера – Капелли). Если система линейных алгебраи-ческих уравнений является совместной, то 
Верно и обрат-ное утверждение.
Если же система линейных алгебраических уравнений совместна, то возможны два случая:
1. Ранг матрицы А равен числу неизвестных системы, т.е. r = п.
В этом случае, отбросив уравнения-следствия, сохраняем коли-чество уравнений, равное числу неизвестных. Затем решаем полученную систему одним из известных методов.
Пример 2. Решить систему уравнений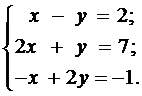 
Здесь
Определим ранг этих матриц:
1 шаг: Прибавим ко 2-ой строке 1-ю строку, умноженную на -2;
к 3-ей строке 1-ю строку;
2 шаг: Прибавим к 3-ей строке 2-ю строку, умноженную на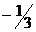 
;
Таким образом, данная система совместна, поэтому оставляем пер-вые два уравнения и решаем полученную систему
Как видим, найденные значения неизвестных удовлетворяют и треть-ему (отброшенному) уравнению.
Замечание 1. Отметим, что можно было, например, отбросив второе уравнение, оставить первое и третье уравнение и, если эта система будет совместной, то решить полученную систему
2. Ранг матрицы А меньше числа неизвестных системы, т.е. r < п.
В этом случае, также отбрасываем уравнения-следствия, оставляя только r уравнений. Но теперь оказывается, что п - r неизвестных явля-ются свободными, т.е. не связанными никакими условиями. Вследствие этого исходная система уравнений имеет бесконечное множество решений.
Для решения такой системы оставим в левых частях уравнений системы r неизвестных с главным определителем, отличным от нуля, а все остальные члены перенесем в правые части уравнений. Затем решим полученную систему одним из известных методов, при этом выбранные r неизвестных будут выражены через п - r свободных неизвестных.
Пример 3. Решить систему уравнений 
Определим ранги основной и расширенной матриц:
1 шаг: Прибавим ко 2-ой строке 1-ю строку, умноженную на -1;
к 3-ей строке 1-ю строку, умноженную на -2;
2 шаг: Прибавим к 3-ей строке 2-ю строку, умноженную на -1;
Таким образом, данная система совместна, поэтому отбрасываем третье уравнение системы и представим ее в виде
Замечание 2. Можно было представить систему и в другом виде
Нетрудно проверить, что найденные решения идентичны.
4.3. Однородные системы линейных алгебраических уравнений
Рассмотрим однородную систему линейных алгебраических уравнений
(2)
Поскольку система (2) всегда совместна, так как 
то вопрос может стоять только о единственности решения системы:
1. Если r = п, то система имеет единственное нулевое решение;
2. Если r < п, то, аналогично, r неизвестных выражаем через остав-шиеся п - r и система имеет бесконечное множество решений;
Пример 4. Решить систему уравнений
Определим ранг основной матрицы:
1 шаг: Прибавим ко 2-ой строке 1-ю строку, умноженную на 2;
к 3-ей строке 1-ю строку, умноженную на -1;
к 4-ой строке 1-ю строку, умноженную на -3;
2 шаг: Прибавим к 3-ей строке 2-ю строку, умноженную на -2;
3 шаг: Прибавим к 4-ой строке 3-ю строку, умноженную на 
;
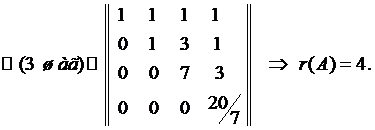
Таким образом, r = п и данная система уравнений имеет единствен-ное нулевое решение
.
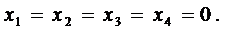ВЕКТОРНАЯ АЛГЕБРА
Лекция № 5. Тема 1: Векторы
1.1. Определение вектора
Все величины, с которыми нам приходилось встречаться до настоящего времени в физике, технике были двух видов: скалярные, которые харак-теризуются одним числовым значением и векторные, - характеризуются числовым значением и направлением.
Пример 1. Скалярные величины: масса, объём, температура и т.д. Векторные величины: сила, скорость, ускорение и т. д.
Определение 1. Направленный отрезок называется вектором и обозна-чается 
. А 
В
Определение 2. Расстояние между началом и концом вектора называется его длиной или модулем и обозначается 
Если 
или 
, то векторы называются соответственно единичным и нулевым.
Определение 3. Векторы называются коллинеарными, если существует прямая, которой они параллельны.
Определение 4. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Определение 5. Два вектора называются равными, если они коллине-арные, одинаково направлены и имеют равные модули (равные длины).
Пусть задан некоторый вектор 
и ось l.
Определение 6. Проекцией вектора на ось l называется величина 
где 
- угол между вектором и осью l.
 |
В
А
l
1.2. Линейные операции над векторами
1. Произведение вектора на число.
Определение 7. Произведением вектора 
на число 
называется вектор 
определяемый следующими условиями: 
вектор 
коллинеарен вектору 
векторы и одинаково направлены, если 
и противоположны, если 
Пример 2. Построить вектор 
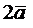
Из этого определения следует условие коллинеарности двух векторов:
Пусть ненулевой вектор, тогда для любого коллинеарного ему вектора существует единственное число 
удовлетворяющее равенству 
Действительно,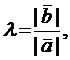 
если векторы одинаково направлены и 
если они противоположно направлены.
2. Сложение векторов.
Определение 8. Суммой двух векторов и называется вектор 
выходящий из их общего начала, который служит диагональю паралле-лограмма, сторонами которого являются векторы и , и обозначается
или
Второй способ построения суммы двух векторов легко распространить на любое число слагаемых. В результате получаем, так называемое правило многоугольника:
Чтобы построить сумму векторов, нужно в конце первого вектора построить второй, в конце второго – третий и т.д. Вектор, соединяющий начало первого с концом последнего и представляет собой искомую сумму.
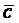
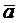
С помощью рисунков легко убедиться в справедливости следующих свойств:
1. 
сложение коммутативно;
2. 
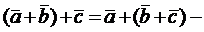ассоциативно.
3. Вычитание векторов.
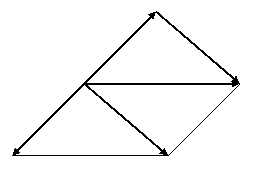
Определение 9. Вектор, коллинеарный данному вектору , равный ему по модулю и противоположно направленный, называется противоположным вектором и обозначается 
Определение 10. Разностью 
векторов и называется сумма векторов и 
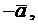т.е. 
Построение вектора 
основано на построении суммы
векторов 
Замечание 1. Из определений 6 и 8 геометрически весьма просто показать следующие свойства:
1. 
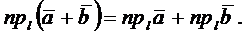
2. 
1.3. Декартова система координат
Зададим в пространстве три единичных взаимно перпендикулярных вектора: 
Приведём их к общему началу – точке О. Рассмотрим систему координат, направление осей: z
О х, О у, О z, которой заданы этими
векторами Такая система
координат называется декартовой M
системой координат. Векторы 
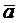
называются базисом, а каждый из 
этих векторов – ортом. 
y
Покажем, что если задан базис O B
, то любой вектор A N
пространства можно единственным x
образом разложить по нему, т.е. представить в виде
(1)
Приведём вектор к началу системы координат – точке О. Из конца вектора - точки М опустим перпендикуляр MN на плоскость О ху. Проведём из точки N прямые, параллельные осям координат. Построим векторы 
Из построения получаем
(2)
А так как 
то выражение (2) примет следующий вид
