Расчет теплового режима анода

Рентгеновской трубки

Как известно, практически вся потребляемая трубкой электрическая мощность преобразуется в тепло, выделяемое на аноде рентгеновской трубки. Поэтому при конструировании рентгеновских трубок необходимо рассчитывать их тепловые режимы. С точки зрения нагрева наиболее критическими являются центр фокусного пятна и центр спая мишени с массивным анодом.

При расчете теплового режима анодов рентгеновских трубок, как правило, вполне допустимо считать, что теплофизические характеристики материалов, из которых изготовлен анод, не зависят от температуры. Для расчета теплофизических характеристик анода можно воспользоваться двумя способами.

 

4.1. Расчет теплового режима массивного анода является важной инженерной задачей, так как при бомбардировке анода электронным пучком почти вся мощность (которая может составлять до нескольких киловатт) расходуется на нагрев анода.

Для решения этой задачи необходимо к необходимо знать формулы расчета теплопроводности. Количество тепла, проходящего через плоскую и цилиндрическую стенки в единицу времени, определяется выражениями:

ккал/ч                 (4.1)

и

ккал/ч               (4.2)

 

где l - коэффициент теплопроводности материала стенок, ккал/м×ч×град; D t – разность температур поверхностей стенки, °С; b – толщина плоской стенки, м; F - площадь плоской стенки, м²; l – высота цилиндрической стенки, м; r ₂, r ₁ – радиусы кривизны наружной и внутренней поверхностей цилиндрической стенки.

 

Охлаждение анодов мощных рентгеновских трубок, работающих в режиме длительных нагрузок, осуществляется проточной жидкостью – водой или маслом.

Количество тепла, передаваемое от охлаждаемой поверхности анода к жидкости в единицу времени, определяется выражением:

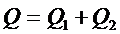                                 (4.3)

где Q ₁ – тепло, отдаваемое торцевой частью охлаждаемой поверхности, ккал/ч; Q ₂ – тепло, отдаваемое цилиндрической частью охлаждаемой поверхности, ккал/ч.

                            (4.4)

где α₁ – коэффициент теплоотдачи торцевой поверхности, ккал/м²×ч×град; F ₁ - площадь торцевой поверхности, м²; t _ст – температура охлаждаемой стенки, °С; t _ж – средняя температура охлаждающей жидкости, °С.

 ,             (4.5)

где l₂ – коэффициент теплопроводности материала анода (для меди l₂ = 330, ккал/м×ч×град); F ₂ – площадь поперечного сечения металлической трубчатой части анода, м²; 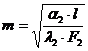, α₂ – коэффициент теплоотдачи цилиндрической поверхности анода, ккал/м²×ч×град;  _- внутренний периметр сечения канала анода, м.

 Коэффициенты теплоотдачи α₁ и α₂ могут быть рассчитаны по формулам:

,                      (4.6)

          

,                   (4.7)

где  безразмерная величина – критерий Рейнольдса, характеризующая режим движения жидкости в подводящей трубке;  критерий Рейнольдса, характеризует режим движения в цилиндрическом зазоре охлаждающей системы; ω₁, ω₂ – скорости движения жидкости в подводящей трубке и цилиндрическом зазоре, м/сек; d ₂ – диаметр сечения отверстия подводящей трубки, м;

 - эквивалентный диаметр цилиндрического зазора, по которому движется охлаждающая жидкость, м; S ₂ – сечение этого зазора, м²; L – его периметр, м;  - критерий Прандля, характеризующий физические свойства охлаждающей жидкости; ν – кинематическая вязкость жидкости, м²/сек; a – коэффициент температуропроводности жидкости, м²/сек; l - коэффициент теплопроводности жидкости, ккал/м×ч×град.

Скорости воды ω₁ и ω₂ могут быть найдены из выражений:

,                                   (4.8)

,                                     (4.9)

где V – расход жидкости, л/мин;  S ₁ – сечение отверстия в подводящей трубке, м²; S ₂ – сечение зазора, м².

При расчете теплоотдачи радиаторов рентгеновских трубок, работающих в защитном кожухе в масле, можно воспользоваться формулой:

 Вт      (4.10)

где t – температура радиатора, °С; t ₀ – температура масла, °С; S - поверхность теплообмена, м²; ς = 1 – при вертикальном положении радиатора; ς = 0.8 – при горизонтальном положении радиатора.

 

4.2. Как известно, практически вся потребляемая трубкой электрическая мощность преобразуется в тепло, выделяемое на аноде рентгеновской трубки. Поэтому при конструировании рентгеновских трубок необходимо рассчитывать их тепловые режимы. С точки зрения нагрева наиболее критическими являются центр фокусного пятна и центр спая мишени с массивным анодом.

При расчете теплового режима анодов рентгеновских трубок, как правило, вполне допустимо считать, что теплофизические характеристики материалов, из которых изготовлен анод, не зависят от температуры.

Если имеем цилиндрический анод радиуса R, и высотой h с массивной мишенью толщиной d, то данную задачу удобнее решать в цилиндрических координатах (см. рис. 1). Допустим, что мишень бомбардируется осесимметричным электронным пучком с радиусом r. Распределение плотности тока в пучке и, следовательно, распределение теплового потока в фокусном пятне на поверхности мишени будем считать равномерным. Как показывает опыт, основание анода является практически изотермическим и будем считать, что с помощью системы охлаждения температура основания Тс1 поддерживается постоянной. Поскольку боковая поверхность массивного анода обычно находится в вакууме, то теплоотводом через нее можно пренебречь.

 

                                                                                                       R

           

 

                                  

 

                              r

 

                                                      d

                                                                  H0

 

                                                                             H

 

Рис. 9. Схема цилиндрического медного анода с вольфрамовой мишенью

 

Для того, чтобы определить тепловой режим работы анода необходимо дифференциальное уравнение с граничными условиями первого и второго рода. Формулы, полученные для расчета температур в результате решения этого уравнения, будут иметь весьма громоздкий вид. Однако для определения мощности, которую можно подвести к аноду, достаточно знать температуру лишь в характерной точке – в центре фокусного пятна. Эту температуру можно рассчитать по следующей формуле:

,                                (1)

где P –подводимая к аноду мощность, R – радиус анода, f_ф – функция, полученная в результате суммирования рядов и зависящая от геометрии анода, радиуса фокусного пятна и коэффициента теплопроводности анода. Т_с – температура в сечении H ₀ = 2R, определяется по формуле:

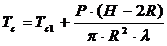,                          (2)                                                

где Т_с1 – температура основания анода, l – теплопроводность анода, H  – высота анода.

 Таким образом, определив температуру Т_с по этой формуле дальнейший расчет следует вести по формуле (1), с применением графика функции f_ф, приведенного на рис. 10.

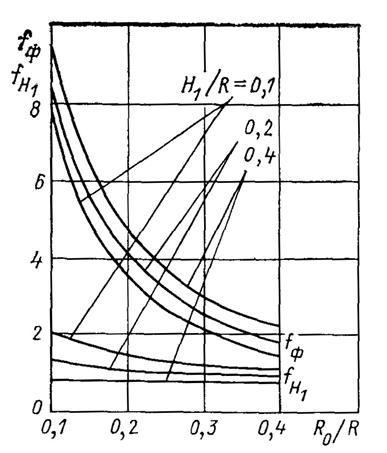
Рис.10. График вспомогательных функций f_ф и f _H1.

Из формул (1) и (2) можно, зная максимально допустимую температуру центра фокусного пятна, вывести максимальную мощность, которую можно приложить к цилиндрическому аноду:

                   (3)

.                                                   (4)

  

Для расчета используются следующие величины:

l 1 - 1.2 Вт/смЧград

l 2 - 3.7 Вт/смЧград

Для вольфрама предельно допустимая температура (Тф) – 2000 ⁰С,

Для меди предельно допустимая температура (Тм) – 800 ⁰С.

Используя указанные величины необходимо определить как температуру центра фокусного пятна, так и максимально допустимую мощность. необходимо определить предельно допустимую мощность трубки (температуры Тф и Тм не должны быть выше предельно допустимых).

При расчете обратить внимание на размерность единиц (не перепутать размерности в таблице, они могут не совпадать с размерностями, используемыми в файле).