I. Последовательность функций комплексных переменных строится следующим образом
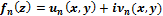
Опр 1. Последовательность 
сходиться в точке 
, если сходится соответствующая числовая последовательность 
. Последовательность называется сходящейся в каждой точке этой области.
Сходимость последовательности в функции комплексных переменных равносильна сходимости 2-м последовательности действия ф-ии 
.
Следовательно, все свойства последовательностей ф-ий справедливы и для сходящихся последовательности в ТФКП.
II. Ряды функции комплексных переменных
Ряд комплексной ф-ии строится:
(6.1)
Ряд (6.1) называется сходящийся в точке 
, если сходится соотв. числовое
Ряд (6.1) называется сходящимся в обл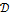 
, если он сходится в каждой точке этой области.
Опр 3. Множество т.z в которых ряд сходится - называется областью сходимости ряда, а предельная ф-ия F (z) называется суммой ряда.
Опр 4. Ряд (6.1) называется сходящимся равномерно F (z), если последовательность его частичных сумм 
сходится равномерно к ф-ии 
в обл. .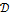
Доказано, что сходимости или расходимость рядов функции комплексных переменных эквивалентно сходимости или расходимости двух рядов действительной ф-ии
Таким образом, все свойства сходящихся рядов действительной ф-ии. Справедливы и для сходимости рядов функции комплексных переменных.
СТЕПЕННЫЕ РЯДЫ
Опр 5. Ряд 
, где 
называется степенным
С помощью замены переменных 
степенной ряд приводится в виду 
поэтому без ограничения общности можно считать, что чтепенной ряд имеет вид: 
(6.2)
Область сходимости степенного ряда яв-ся: 1. Одна точка, 2. Круг, 3. Вся комплексная плоскость
Первая теорема Абеля. Если степенной ряд (6.2) сходится в т. 
то, 1) этот ряд сходится абсолютно в круге 
; 2) в круге 
ряд сходится равномерно 
Следствие из теоремы: если степенной ряд (6.2) в точке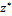 
расходится, то этот ряд расходится в области 
Доказательство:
Теорема
Для любого степенного ряда (6.2) существует число 
зависящая от ряда такая что: 1) в круге 
ряд сходится, 2) в области 
ряд расходится
Предельные случаи: 
R=0 – ряд сходится в точке 
, ряд расходится в обл-и 
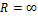- ряд сходится всюду в 
Опр 2. Число Rудобл. условиям теоремы называется радиусом сходимости ряда (6.2).круг K называется кругом сходимости ряда.
Формула Коши-Адамара для радиуса сходимости R
Замечание! На границе круга К ряд (6.2) в некоторых точках может расходится, а в некоторых точках может сходится требуются дополнительные исследования.
