1.Последовательности
Для задания последовательности к.ч. необходимо задать 2 последовательности действительных чисел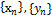 
,тогда 
Определение 1.К.ч. а 
, если для 
| 
|< 
В случае а= 
| 
|>
Определение2.Последовательность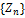 
,имеющая конечный предел(а 
) называется сходящимся,в противном случае расходящийся.
Теорема: Пусть :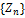 
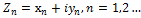a=x+iy а 
Док-во:
Необходимость: Пусть 
| |<
| 
|<
| 
|<
=> 
=>
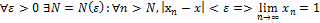
Достаточность: 
N=max(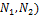
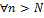
Из теоремы следует, что все свойства сходимости последовательности действительных чисел справедливы для сходящихся последовательностей к.ч.
2.Ряды к.ч.
Ряд к.ч. образуется сл. образом
(3.1)
Определение3.Ряд (3.1) называется сходящимся, если сходится последовательность его частичных сумм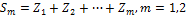 
при этом 
Определение 4.Ряд (3.1) называется сходящимся абсолютно, если сходится ряд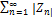 
- ряд моделей к.ч.
Если ряд(3.1) сходится, он не абсолютно, то говорят, что он сходится условно. Т.к. сходимость ряда к.ч. эквивалентна сходимости последовательности к.ч., которая в свою очередь эквивалентна сходимости последовательностей действ. Чисел, то сходимость ряда к.ч. эквивалентна сходимости двух рядов действ.чисел.
Все св-ва сходимости рядов действ.чисел, кроме свойств связанных с неравенствами справедливо для сходящихся рядов к.ч.
4. Функции комплексного переменного.
Опредение_1.
Пусть М ≠ø, если каждому значению z из множества М (z ϵ M) поставлены соответствия по некоторому закону f один или несколько комплексных чисел w, то говорят, что на множестве M задана функция w = f (z).
Определение_2.
Если каждому значению z ϵ M, за исключением некоторого конечного числа значения z, поставлено соответствие n - различных значений w, то функция называется n -значной.
, 
, 
1) 
Каждой паре (x, y) ϵ Ȼ на комплексной плоскости соответствует одно значение u (x, y) и одно значение v (x, y). =>Функция w=z2 – однозначная функция на множестве ₵.
2) 
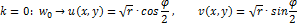
3) 
4) 
-значная функция, 
.
5.Производня функции комплексного переменного. Аналитические функции.
Определение 1.
Пусть функция f (z) определена в некоторой окрестности точки z 0, тогда f (z) называется дифференцируемой в точке z 0, если 
существует и не зависит от способа стремления точки z к z 0.
Значение этого предела называется производной функции f (z) в точке z 0: 
.
Так как комплексный предел равносилен двум действительным пределам, то все правила дифференцирования действительной функции справедливы для комплексной функции.
Например,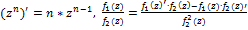 
.
Определение 2
Функция f (z) называется аналитической в точке z 0, если она дифференцируема в некоторой окрестности этой точки. Функция f (z) называется аналитической в области D, если она является аналитической в каждой точке этой области. Таким образом, функция f (z) аналитична в области D тогда и только тогда, когда она дифференцируема в этой области.
Элементарные свойства аналитических функций:
1) если функция аналитична в области D, то она в ней непрерывна;
2) сумма, разность, произведение, частное (при условии, что знаменатель равен 0) в нескольких аналитических функций, есть аналитическая функция;
3) суперпозиция конечного числа аналитических функций, есть аналитическая функция.
Теорема Коши-Римана.
аналитична в области Dó
1) 
2) 
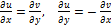- условия Коши-Римана.
Следствие 1.
Если функция f (z) аналитична в области D, то её производную можно найти по формулам:
- аналитична на всей комплексной оси
- функция не является аналитической
Следствие 2.
Если u (x, y) – действительная часть некоторой аналитической функции, то мнимую часть этой функции можно найти по формуле: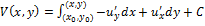 
, где (x 0, y 0) – фиксированная точка области D, (x, y) – переменная точка области D.
Криволинейный интеграл берётся по пути полностью лежащей в области D.
