Пусть 
кусочно-гладкая ориентированная кривая имеющая длину 
в концах а и b, если а=b, то кривая -замкнутая.
Пусть на любой 
заданны функция f(z), 
произведено разбиение кривой 
Возьмем произвольным образом величину 
и составим интегральную сумму
Определение 1:Если существует предел при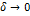 
(
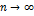) и этот предел не зависит от способа стремления 
(способа деления кривой на части) то этот предел называется интегралом от функции f(z) по контуру .
Если замкнутая кривая, то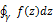 
замкнутый контур.
Свойства Интегралов:
1)Интеграл зависит от ориентации кривой, если направление -от a к b, то
2)Задание интеграла от функции комплексных переменных эквивалентно заданию 2-х вещественных криволинейных интеграла.
f(z)=U(x,y)+iV(x,y)
Доказательство:
Dz=d(x+iy)=dx=idy
3)Свойство линейности интеграла
Если функция 
,k= 
, интегрируемые на контурах 
,то
4)Свойство аддиативности интеграла относительно контура
Если можно представить в виде объединения промежутков (
, причем контуры 
пересекаются но не имеют общих частей, то интеграл от функции:
5)Оценка модуля интегралов:
M=maxf(z), -длина .
6)Если функция f(z) и 
интегрируемые на 
причем 
, 
7)Переход к пределу по знаку интеграла.
Если на 
заданны последовательность интегрируемых функций 
, равномерно сходящихся 
же интегрируемая по , то
8)Почленное интегрирование равномерно сходящегося ряда
Если на заданна равномерно сходящиеся ряд с 
c предельной функцией f(z) и все функции 
и f(z) интегрируемы на , то
Интегральная теорема Коши и ее обобщения.
Теорема: пусть D - ограниченная односвязная область, f(z) - аналитична в D, γ - произвольный замкнутый гладкий контур, принадлежащий области D, тогда 
Другая формулировка теоремы: если функция f(z) аналитична в ограниченной односвязной области D, то ее интеграл не зависит от пути интегрирования, а лишь от пределов интегрирования(концов кривой) a и b.
Доказательство эквивалентности двух формулировок теоремы: 
, (
- движение по 
осуществляется в противоположном направлении).
Тогда по свойству 4(в.11) 
, по свойству 1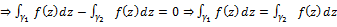 
Доказательство того, что из второй формулировки следует первая проводится в обратном порядке.
Обобщение 1. Пусть D - односвязная ограниченная область с кусочно-гладкой границей 
. Функция f(z) аналитична в области и непрерывна в замкнутой области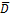 
, тогда 
Обобщение 2. Пусть D - многосвязная ограниченная область с кусочно-гладкой границей 
. Функция f(z) аналитична в области и непрерывна в замкнутой области 
, тогда 
